
- •Глава 1
- •10.Квадратичная форма и полярная билинейная форма.
- •20. Матрица квадратичных форм.
- •30. Ограничение билинейной (квадратичной формы) на подпространстве
- •10.Определние ортогональности относительно билинейной формы и свойства.
- •20.Ортогональное дополнение и его свойства
- •Глава 2
- •Глава 3
- •1° Теорема об изоморфности евклидовых (унитарных) пространств
- •2° Линейные формы в евклидовых(унитарных) пространствах и скалярные произведения
- •10 Определение и первый критерий
- •20 Ортогональные операторы и ортонормированные базисы
- •30 Ортогональный оператор и сопреж. К немк (Кр-3)
- •40 Матрица ортог. Оператора
- •Глава 4
- •1° Определения и примеры
- •2° Леммы о высшем члене симметрического многочлена
- •3° Основная теорема о симметрических многочленах
10 Определение и первый критерий
Определение. Изоморфизм Евклидова пр-ва на себя называется ортогональным оператором, таким образом ортогональный оператор линейный биективный и сохраняет скалярное произведение
Теорема(Критерий 1)
F : En → En - явл. Ортогональным <=>сохраняет скалярное опред.
,,=>” по опр.
,,<=” достаточно доказать биективность f поскольку f действует из Еn в Еn то достаточно доказать его инъективность.
Пусть a, f ϵ En и f(а)=f(в); <=> f(a)-f(в)=0 <=> f(a-в)=0
(a-в)•(a-в)=f(a-в)•f(a-в)= 0•0=0 => a-в=0 a=в – значит инъективно
20 Ортогональные операторы и ортонормированные базисы
Теорема (Критерий2)
Лин. Опр-р
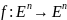 ортогон.<=> когда он переводит ортонорм.
б. в ортонорм базис.
ортогон.<=> когда он переводит ортонорм.
б. в ортонорм базис.
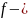 сохр. ск. пр-е а значит сохр. ортогон-ть
векторов и длина векторов поэтому если
сохр. ск. пр-е а значит сохр. ортогон-ть
векторов и длина векторов поэтому если
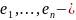 О.Н.Б , то
О.Н.Б , то
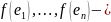 ?
попарно ортогон-х векторов единичной
длины.
?
попарно ортогон-х векторов единичной
длины.
Ранее было пок. что сов-ть попарно ор-х длин нез. век. и что это набор лин. нез. и это базис т.к
кол-во совпад. с разм-ю.
“<=”
лин. оператор
ортон.
б.
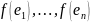 - ортон. б.
- ортон. б.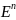 сыл.
кр-1 чтобы пок. что
сыл.
кр-1 чтобы пок. что
 ортог.
чтобы он сохр. скалярное произв-ею
ортог.
чтобы он сохр. скалярное произв-ею
Пусть a,b
э
а =
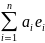 ,
b =
,
b =
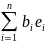 тогда аb=
тогда аb=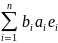 т.к
О.Н.Б
т.к
О.Н.Б
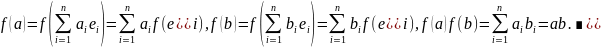
30 Ортогональный оператор и сопреж. К немк (Кр-3)
Tеорема.
Линейный опер.
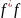 =1
когда опер.
ортог
сохр. скалярное пр-е.
a,b из E -
=1
когда опер.
ортог
сохр. скалярное пр-е.
a,b из E -
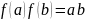
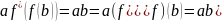 .
a,b из Е
.
a,b из Е
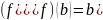
b из
b из
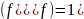
40 Матрица ортог. Оператора
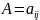 ортогон. если
ортогон. если
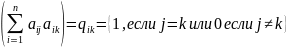
В матричной форме это означает АТ А=Е
Теорема. Линейный оператор Евклидова пр-ва явл-ся ортогональным <=> когда его матрица в ортонорм. базисе ортогональна.
согласна КР3. ортогональность оператора f <=> f*f= A Если А- матрица f в некотором ортонорм. Базисе, то ранее мы доказали что матр. F* в таком же базисе будет Ат ; рав-во (*) в матр. Ор. Принимает вид Ат А=Е
Гл 3. Пр.4 Инвариантные подпр-ва и канонич. вид матрицы ортогон. оператора.
Ортогон. дополн. подпр-ва, инв-го отн-но ортогон. оператора.
Теорема.
Пусть W- подпр-во
,
инв-ое отн-но ортогон. оператора f
на
.
Тогда
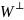 также явл. инв-ым отн-но f.
также явл. инв-ым отн-но f.
Пусть
f(W)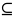 W.
инв. отн. f*, т.е. инв-но отн.
W.
инв. отн. f*, т.е. инв-но отн.
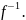 Это значит, что
Это значит, что
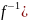 )
)
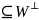 .
Поскольку
.
Поскольку
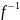 невырожд., то
)
невырожд., то
)
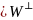 .
Применим к посл. рав-ву оператор f:
f(
))=f(
)
.
Применим к посл. рав-ву оператор f:
f(
))=f(
)
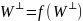 ⇒ f(
)
– инв-но ⇒
инв-но отн-но f.
⇒ f(
)
– инв-но ⇒
инв-но отн-но f.
Лемма об 1,2-мерных подпр-вах, инв. отн. лин. оператора.
Лемма. не нулевого, лин. оператора f действ. пр-ва V инв-ое отн. f 1-мерное или 2-мерное подпр-во.
Пусть
у f
собств.вектор a
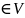 .
Тогда L(а) – искомое
1-мерное подпр-во. действительно f(а)=
.
Тогда L(а) – искомое
1-мерное подпр-во. действительно f(а)=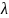 a,
где
-собств.
значение. Поэтому
х
L(a), т.е. х=αa
(α
a,
где
-собств.
значение. Поэтому
х
L(a), т.е. х=αa
(α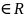 ),
f(x)=f(αa)= αf(a)=
α
a, α
a
L(a) ⇒
f(L(a))
L(a).
Предпол. что действ. собств. вектора
),
f(x)=f(αa)= αf(a)=
α
a, α
a
L(a) ⇒
f(L(a))
L(a).
Предпол. что действ. собств. вектора
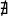 ⇒
собств. знач., т.е. характ. мн-н не имеет
действ. корней. Но имеет
⇒
собств. знач., т.е. характ. мн-н не имеет
действ. корней. Но имеет
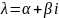 -компл. корень характ. мн-на и c=a+bi
–соотв. ему компл. вектор (a,b
-действ. векторы).
-компл. корень характ. мн-на и c=a+bi
–соотв. ему компл. вектор (a,b
-действ. векторы).
F
–матрица f; C=A+Bi
-- вектор столбец, коорд. вектора с в
том же базисе. Тогда f(c)=
c
в матр. Форме ⇔
F(A+Bi)=(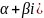 (A+Bi);
(A+Bi);
FA+FBi=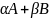 +(
+(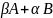 )i;
)i;
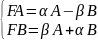 Данное матр. данное означает: (+)
Данное матр. данное означает: (+)
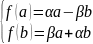 ,
,
Где a,b – векторы, имеющие в данном базисе вектор-столбцы коорд. А,В.
Система (+) пок-т, что L(a,b) инв. отн-но f.
Т. о разлож. в прямую сумму подпр-в, инв-х отн. ортогон. опер-ра.
Теорема. Пусть f-ортогон. оператор , тогда -прямая сумма попарно-ортогон-х 1-мерных или 2-мерных подпр-в инв. отн-но f.
Индукция по n=dim
База индукции n≤2
Индукционный переход. Предпол., что утв. верно для пр-в разм-ти <n. Док-м, что тогда оно верно и для разм. n.
В
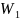 (dim
=1,2)
инв. отн. f. Тогда
=
(dim
=1,2)
инв. отн. f. Тогда
=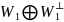 , причем
, причем
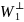 -инв.
отн-но f. Поэтому ограничение
-инв.
отн-но f. Поэтому ограничение
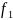 оператора f на
явл. лин. оператором на
,
причем поскольку
(x)=f(x),
х
,
то
явл. ортогон. операт. на
.
оператора f на
явл. лин. оператором на
,
причем поскольку
(x)=f(x),
х
,
то
явл. ортогон. операт. на
.
Т.к. dim
<n,
то согл. инд. предпол.
=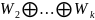 попарноортогон. подпр-в разм-ти 1 или 2,
инв-х отн.
.
Поскольку на этих подпр-х
попарноортогон. подпр-в разм-ти 1 или 2,
инв-х отн.
.
Поскольку на этих подпр-х
 на
на
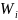 ,
то они инв-ны также и отн. f.
Поэтому
,
то они инв-ны также и отн. f.
Поэтому
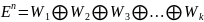 - искомое разложение.
- искомое разложение.
Собств. знач. и определитель ортогон. оператора.
Предложение 1. Действ. собств. знач. ортогон. оператора (ортогон. матрицы) равны ±1.
Пусть а-собств.вектор ортогон. оператора f, - соотв. собств. знач.
aa=f(a)f(a)=(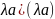 =
=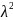 (aa),
a - собств.
вектор ⇒
a
0
⇒
aa
0
⇒
=1
⇒
=±1.
(aa),
a - собств.
вектор ⇒
a
0
⇒
aa
0
⇒
=1
⇒
=±1.
Предложение 2. Определитель ортогон. матрицы detA=±1.
Пусть
А-ортогон. матрица. По опр.
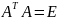 ;
det(
;
det(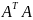 )=1;
det(
)=1;
det(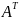 )detA=1;
)detA=1;
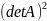 =1
⇒ detA=±1.
=1
⇒ detA=±1.
 Ортогон.
операторы
Ортогон.
операторы
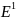 и
и
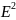 .
.
Предложение 1. В пр-ве только 2 ортогон. оператора: f(x)=x, f(x)=-x.
f
– ортогон. оператор в
.
Поскольку f – ортогон.,
то f(x)=
x
для некоторого
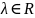 ⇒
- собств. знач.,
=±1
⇒ f(x)=x
⇒
- собств. знач.,
=±1
⇒ f(x)=x
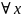 ,
или f(x)=-x
,
или f(x)=-x
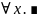
Предложение
2. В
любой ортогон. оператор имеет в подходящем
ОНБ матрицу
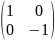 или
или
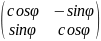 для некоторого
для некоторого
 .
.
А-матрица ортогон. оператора f в некотором ОНБ ⇒ А – ортогон. ⇒ detA=±1.
detA=-1;
А=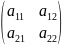 Рас-м характ. мн-н этой матрицы
Рас-м характ. мн-н этой матрицы
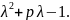 свободный член – оределитель.
свободный член – оределитель.
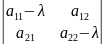 =(
=(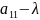 )(
)(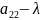 )-
)-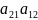 =
=
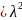 -(
-(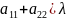 +(
+(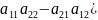 =
=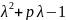 ⇒ Характ. мн-н
имеет 2 корня(+ и - ) ⇒
⇒ Характ. мн-н
имеет 2 корня(+ и - ) ⇒
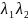 =-1;
D>0; (
=-1;
D>0; (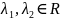 )
⇒
)
⇒
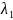 =1;
=1;
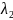 =-1.
=-1.
Пусть
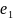 ,
,
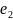 - единичные собств. векторы, отв-е этим
собств. знач.
- единичные собств. векторы, отв-е этим
собств. знач.
f(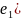 =
,
f(
)=
.
В данном базисе
,
матрица:
=
,
f(
)=
.
В данном базисе
,
матрица:
detA=1;
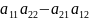 =1
……(1)
=1
……(1)
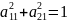 …..(2);
…..(2);
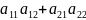 =0
……(3) ;
=0
……(3) ;
Из (2) ⇒
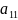 =
=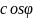 ;
;
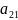 =
=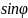 ,
для некоторого
.
,
для некоторого
.
Из равенств
(1),(3) ⇒
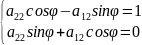
Det=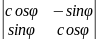 =1≠0
⇒ сущ. единств.
реш-е
=1≠0
⇒ сущ. единств.
реш-е
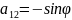 А=
А=
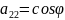
 Канонический
вид матрицы ортогон. оператора.
Канонический
вид матрицы ортогон. оператора.
Теорема.
ортогон. оператора f: ОНБ
в котором f имеет матрицу
вида:
ОНБ
в котором f имеет матрицу
вида:
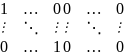


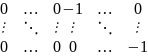 (*)
(*)
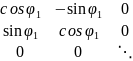
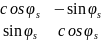
Пр-во
представляется как
-прямая сумма попарноортогон. 1,2-мерных
подпр-в, инв-х отн. ортогон. оператора
f. Ограничение f
на каждое подпр-во
само явл. ортогон. оператором на этом
подпр-ве.
ОНБ
в каждом
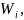 в которых это ограничение оператора f
имеет матрицу вида:
в которых это ограничение оператора f
имеет матрицу вида:
(1), (-1), ,
Объединив все эти базисы получим базис всего пр-ва, в котором f имеет клеточно-диагональную матрицу с диаг. эл-ми, указанного выше вида. Изменив при необх. Порядок базисных эл-ов, можно получить матрицу вида (*).
Следствие.
Всякая ортогон. матр. А ортогонально
подобна некоторой матрице вида (*). (т.е.
ортогон. матрицы А
ортогон. матрица С |
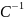 АС=В
- имеет вид (*)).
АС=В
- имеет вид (*)).
Пусть f- оператор на с ортогон. матр. А ⇒ f – ортогон. Согл. Т. ОНБ, в котором f имеет матрицу В вида (*).
Пусть С- матрица перехода от того ОНБ, в котором f имел матрицу А, к тому ОНБ, в котором f имеет В. Согл. преобр. АС=В (+), т.к. С – матрица перехода от ОНБ к ОНБ, то она ортогональна.
Замечание.
Поскольку для ортогон. матрицы
=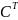 ,
то (+):
АС=В.
,
то (+):
АС=В.
Гл3 Пр5 Унитарные Операторы
Определение, критерии и матрица унитарных операторов.
Определение.
Изоморфизм унитарного пр-ва
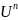 называется унитарным оператором.
называется унитарным оператором.
Теорема
1: Линейный оператор f: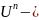 >
является унитарным <=> он сохр.
Скалярное произведение.
>
является унитарным <=> он сохр.
Скалярное произведение.
Теорема
2: Линейный оператор f:
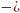 >
является унитарным <=> он
переводит ортонормированный базис в
ортонормированный.
>
является унитарным <=> он
переводит ортонормированный базис в
ортонормированный.
Теорема
3: Линейный оператор f:
>
является унитарным <=> f*f=
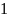 (Тождественный оператор)
(Тождественный оператор)
Определение : Каждая матрица называется унитароной, ести A*A=E, где А*= Āᵗ.
Теорема: f: > <=> его матрица в ОНБ
 f-унитарный <=> f*f=
f-унитарный <=> f*f=
A*A=E, А – матрица f.
Инвариантроне пр-во и конечный вид матрицы ун-го оператора.
Теорема1: W – подпространство , инвар. относ. f: > .
Тогда W┴ инвариантно относ. f.
Предложение 2: β – единственное собств. значение унитарного оператора f. Тогда | β |=1.
а- собственный вектор, соотв. β .
а·а=f(a)·f(a)=(βa)·(βa)=| β |²(a·a)
a≠0=>а·а≠0, тогда | β |²=1 =>| β |=1
Предложение 3: А- унитарная матрица, тогда |det A|=1
Согласно определению унитарной матр. Имеем A*A=E.
Det(A*A)=1 => det A*·det A=1 => det Ā·det A=1 => |det A|²=1 => |det A|=1
Теорема: f унитарный оператор f: > . Существует ОНБ пр-ва в которой f имеет унитарную матрицу diag(β1, … , βn) где |βi|=1.
Следствие:
Любая унит. Матрица А унитарно подобна
диагональной матрице B=diag(β1,
… , βn) где |βi|=1.
Т.Е. для любой унит. матр А существует
унитарная матрица С |
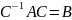 , где B=diag(β1,
… , βn) где |βi|=1.
, где B=diag(β1,
… , βn) где |βi|=1.
Гл3 Пр6 Самосопряженные операторы в евклидовых и унитарных пространствах
Определения и матрицы
Определение. Пусть f: V͢͢͢͢V, где VEn(или Un) f. – наз. самосопряженным, если fn=f
Теорема: Пусть f:VV – лин. оператор, А – матрица f в ОНБ.
Если V=En, то f – самосопряженое A= At – самосопряженная матрица
Если V=Un, то f – самоспряженное A=A* - эрмитова матрица
A-f, то At – f* (V=En)
A* - f* (V=Un)
f=f* в матр. виде At=A или A*=A.
Инвариантные подпро-ва относительно самосопряж. оператора
Теорема: Пусть W – подпр-во En или Un инвариантно относительно самосопряж. оператора f, тогда W° так же инвариантно относительно f.
Док. W° инвариантно относительно f*
f*=f => W° инвариантно относительно f.
Предложение: При любом самосопряжении оператора f на En или Un сущ. одномерное подпр-во инвариантно относительно f
En, W – 2-мерное подпр-во инвариантное относительно f
f1 – ограничение f на W
f1* = f1 (f1 – f на W)
f1* - симметр.
A= (a11 a21)
(a21 a22)
Характеристический многочлен этой матрицы:
|a11-λ a11|
|a21 a22-λ| = λ2-(a11-a22)λ+a11a22-a122
Д=(a11-a22)2-4(a11a22-a122)=(a11+a22)-4a11a22+4a122=(a11-a22)2+4a122 >= 0
Существуют действительные корни. Пусть λ – один из них
a – собственный вектор W соответствующий собственному значению λ
L(a) – одномерное подпр-во инвариантное относительно f => инвариантно относительно f.
Конанический вид матрицы
Теорема: Пусть V En или Un
F – самосопряженный оператор на V
Тогда V – является прямой суммой попарно ортагональных одномерных подпр-тв инвариант. относительно f
Такое же как и для ортагонал. и унитар. операторов.
Теорема: Любое самосопряж. оператора пространство En или Un существует ОНБ состоящий из собственных векторов оператора f. Матрица в этом базисе диагональная с собственным значением на диагонали.
Такое же как и для ортагонал. и унитар. операторов.
Следствие: Всякие действ. симметрическая (комплекс. эрмитова) матрица ортагонально (унитарно) подобна некоторой действительной ортагональной матрице.
A сущ. ортагон. (унитарн.) принадлежит / B=C-1AC – диагонал.
Гл 3 Пр7 Приведение квадратичной формы к каноническому виду ортогональным преобразованием
Теорема
Теорема.
квадратичной формы F(x)
преобразование X=CY
с ортогональной матрицей С, приводящей
квадратичную форму к каноническому
виду:
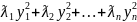 ,
где
,
где
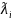 -собственное
значение матрицы квадратичной формы
F(x)
-собственное
значение матрицы квадратичной формы
F(x)
пусть
А – матрица квадратичной формы F(x),
тогда А – действительно симметрическая,
значит, диагонально подобна ортогональной
матрице т.е. ∃
ортогональная матрица С |
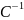 AC=В,
где В=diag(
AC=В,
где В=diag(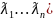 ,
где
,
где
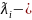 собственное
значение матрицы А на диагонали. Применим
к F(x) линейное
преобразование X=СУ, тогда
матрица квадратичной формы будет равна
собственное
значение матрицы А на диагонали. Применим
к F(x) линейное
преобразование X=СУ, тогда
матрица квадратичной формы будет равна
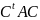 =
=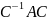 =
diag(
=
diag(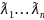 )
)
Приведение к каноническому виду пары квадратичных форм
Теорема. Пусть F(x), G(x) – квадратичные формы, причем F(x) положительно определена, тогда невырожденное линейное преобразование переменных, которое приводит каждую из этих форм к каноническому виду.
т.к.
F(x) –
положительно определена, то
невырожденное линейное преобразование
Х=ТУ, которое приводит квадратичную
форму F(x) к
нормальному виду: F(x)=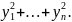 Матрица квадратичной формы равна Е. Это
же преобразование приводит G(x)
к некоторому виду
Матрица квадратичной формы равна Е. Это
же преобразование приводит G(x)
к некоторому виду
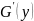 .
Можно привести линейное преобразование
Y=CZ к
каноническому виду (С-ортогональная
матрица). После преобразования квадратичная
форма F будет иметь матрицу
.
Можно привести линейное преобразование
Y=CZ к
каноническому виду (С-ортогональная
матрица). После преобразования квадратичная
форма F будет иметь матрицу
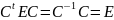 ,
т.е. ее вид не изменится и канонический
вид будет:
,
т.е. ее вид не изменится и канонический
вид будет:
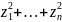 ,
таким образом X=(TC)Z
приводит обе эти квадратичные формы к
каноническому виду.
,
таким образом X=(TC)Z
приводит обе эти квадратичные формы к
каноническому виду.
Гл 3 Пр8 Полярное разложение
Определение. Полярное разложение – это разложение линейного оператора в произведение ортогонального и самосопряженного.
Теорема.
невырожденного линейного оператора f
на евклидовом пространстве
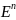 ортогональный оператор h
и самосопряженный оператор g
на
ортогональный оператор h
и самосопряженный оператор g
на
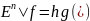
(доказательство включает в себя лемму с доказательством): пусть (*) имеет место. Выясним, каким должен быть g.
f*=(hg)*=g*h*=g,
тогда f*f=g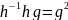 ,
значит, g должен быть
таким, что
,
значит, g должен быть
таким, что
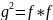 .
(**)
.
(**)
Лемма: пусть f – невырожденный линейный оператор на , тогда f*f – самосопряженный, все собственные значения которого положительны.
: (f*f)*=f*(f*)*=f*f, ƛ-собственное значение f*f, a – собственный вектор. (f*f)(a)·a=(ƛa)·a=ƛ(a·a)
(f*f)a·a=f*(f(a))·a=f(a)·f(a)
ƛ(a·a)=f(a)·f(a).
ƛ(a·a)>0 и f(a)·f(a)>0, следовательно ƛ>0.
Покажем, что самосопряженный оператор g, удовлетворяющий условию (**), существует:
т.к. f*f
– самосопряженный, то
ортонормированный
базис пространства
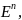 в
котором матрица f*f:A=diag(
в
котором матрица f*f:A=diag(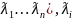 -собственное
значение оператора f*f.
Рассмотрим матрицу В=diag(
-собственное
значение оператора f*f.
Рассмотрим матрицу В=diag(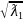 ,…,
,…,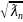 )
(ƛ>0)
)
(ƛ>0)
g-оператор
с матрицей В. В-симметрическая,
следовательно g –
самосопряженный, причем
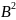 =A,
=A,
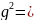 f*f,
т.о. g – искомый оператор.
f*f,
т.о. g – искомый оператор.
Покажем, что
h: h однозначно
определяется из равенства f=hg,
нужно доказать, что h –
ортогональный: h*h=(f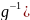 *f
*f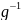 =(
*f*f
=
=(
*f*f
=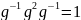 (тождественная единица)
(тождественная единица)
Следствие: всякая невырожденная действительная матрица А раскладывается в произведение A=HG, где H-ортогональная матрица, G-симметрическая.
