Глава 3

Гл3 Пр1 Линейные операторы и линейные формы

Пусть заданы V и V’ над Р, то линейным оператором называется такое f:V—>V’, что

f(a+b)=f(a)+f(b) , a,b є V

f(λa)=λf(a) для любого λ є V, а є V

если кроме того f биекция, то его называют изоморфизмом , а V, V’ – изоморфными.

1° Теорема об изоморфности евклидовых (унитарных) пространств

Пусть V, V’ – евклидовы(унитарные) пространства. Биективное линейное отображение f:V—>V’ называется изоморфизмом евклидовых(унитарных) пространств, если оно сохраняет скалярное произведение, т.е. , a,b є V f(a)∙f(b)=a·b

Теорема 2 евклидовых(унитарных) пространства изоморфны  когда из размерности совпадают

“<=” Пусть dim V= dim V’ = n ; 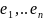-базис V ; 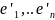_– базис V’ ; базисы V и V’ ортонормированны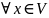 , 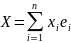f(x)= 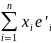при этом отображении свойства линейности сохраняются, т.к. базисы ортонормированны, то скалярное произведение сохраняется, в силу невырожденности f-биекция => f-изоморфизм.

“=>” Пусть V и V’ изоморфны и f-изоморфизм; покажем что тогда они имеют одинаковую размерность. Dim V=n -базис V. Приравняем к 0 линейную комбинацию этих векторов.

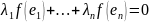
Пусть 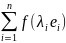 =0. Поскольку f-невырожденный,то такое равенство возможно если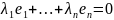 , т.е. , i=1..n =>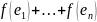 – линейно независимы => dim V’≥n=dim V. Поскольку для f существует f^-1 , то рассмотрим f^-1 :V’—>V получим dim V≥dim V’ => dim V=dim V’=n

2° Линейные формы в евклидовых(унитарных) пространствах и скалярные произведения

Теорема Пусть f:V—>R(C) – линейная форма на пространстве V=Eⁿ (uⁿ )Тогда существует единственный вектор aєV f(x)=x∙a для любого x єV

Пусть - ортогональный базис пространства V. И пусть в этом базисе f(x)=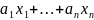 . Определим a=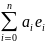 ,но тогда x∙a действительно x∙a = =f(x)

Предложение Пусть a,b є Eⁿ (uⁿ ). Если для любого x є Eⁿ (uⁿ ) имеет место x∙a= x∙b , то a=b.

x∙a= x∙b  x∙a - x∙b = 0  x∙(a-b)=0  (a-b)(a-b)=0 => a-b=0 => a=b

Гл3 Пр2 Сопряженные операторы

Определение.Теорема о существовании и единственности.

Определение. f:V->V лин.оператор на пространстве V=Eⁿ(Uⁿ)

f^*:V->V наз. сопряжённым к f,если x,y V, f(x) y=x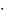 f^*(y)

Теорема. Сопряжённый оператор к оператору f на Eⁿ(Uⁿ) существует,единственный и линейный.

1.существование

Fix y V(V= Eⁿ или Uⁿ)

Рассмотрим линейную форму α на V,заданную след.образом:

α(x)=f(x) y.Такое отношение является линейной формой в силу лин. F и скал.произведения.

Определим f*(y)=a.

В силу единственности a для любой конкретной формы α(x) такое отображение задано корректно.

f(x) y=α(x)=x a=x f^*(y)

2.существование

F₁^* - ещё один сопряжённый для f

x,y V, x f^*(y)=f(y) y=x f₁^*(y) => f^*(y)=f₁^*(y)

Т.е. f^*=f₁^*

3.линейность

Пусть λ₁,λ₂ ℝ(ℂ)

Пусть y₁,y₂ V ,f^*( λ₁ y₁+ λ₂ y₂)= λ₁f^*(y₁)+ λ₂f^*(y₂)

Пусть x V ,x f^*( λ₁ y₁+ λ₂ y₁)=f(x) ( λ₁ y₁+ λ₂ y₁)= λ₁(f(x) y₁)+ λ₂(f(x) y₂)= λ₁(x f^*( y₁))+ +λ₂(x f^*( y₂))=x ( λ₁f^*( y₁)+ λ₂f^*( y₂))

x V ,f^*( λ₁ y₁+ λ₂ y₂)= λ₁f^*( y₁)+ λ₂f^*( y₂)

Свойства сопряжённого оператора

1. 1^*=1 (1-сопряжённый оператор)

2. (f)^*=f

3. (f+g)^*=f^*+g^*

4. (λf) ^*=λf^* (в Eⁿ)

(λf) ^*= λ(сопряжённое)f^*

5. (fg)^*=g^*f^*

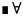x,y V, x (fg)^*(y)=(fg)(x) y=f(g(x)) y=g(x) f^*(x)=x g^*(f^*(y))=x (g^*f^*)(y)

=>(fg)^*=g^*f^*

6. (f^-1)^*=(f^*)^-1

(f^-1)^*f^*=(f*f^-1)^*=1^*=1,т.е. (f^-1)^*-обр. к f^*

Значит (f^-1)^*=(f^*)^-1

Сопряжённые операторы и инвариантные подпространства.

f(W) содержится в W

Теорема. Пусть f:V->V – лин. оператор (V= Eⁿ или Uⁿ)

W – инвариантное подпространство пространства V отн. F

Тогда W(ортогон.) – инвариантно отн. F^*.

Матрица сопряжённого оператора

Теорема. A – матрица f на V

(V=Eⁿ,Uⁿ) в ортонормированном базисе.

Тогда матрицей f^* в этом же базисе является A^*,если V=Uⁿ

И A^T,если V=Eⁿ

Гл3 Пр3 Ортогональные операторы