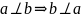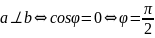Глава 2
Гл 2 Пр 1 Скалярное произведение на векторном пространстве
Евклидовы пространства
Определение.
V- действительное линейное
пространство. Скалярным произведением
на V называется отображение,
которое
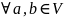ставит в соответствие действительное
число
,
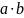причём выполняются свойства:
1.
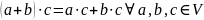
2.
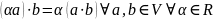
3.
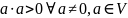
4.
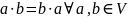
Из условия 4 и 1,2 вытекает, что:
1.'
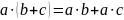
2.'
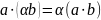
Замечание. Свойства 1 и 2, 1' и 2' показывают, что скалярное произведение является билинейной формой. Свойство 4 показывает, что эта форма является симметрической. А свойство 3 показывает, что порождённая этой формой квадратичная форма является положительно определённой.
Из свойств 1 и 2, 1' и 2' вытекает общее свойство линейности скалярного произведения
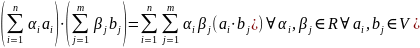
Примеры.
1.
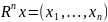
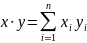
2.
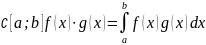
Определение. Действительное линейное пространство, на котором задано скалярное произведение называется евклидовым пространством.
Замечание. Всякое подпространство евклидова пространства также является евклидовым относительно сужения скалярного произведения на него.
Унитарные пространства
Определение. V- комплексное линейное пространство. Скалярным произведением на V называется отображение, которое ставит в соответствие комплексное число , причём выполняются свойства:
1.
2.
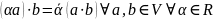
3.
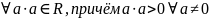
4.
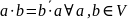
Из условия 4 и 1,2 вытекает, что:
1.'
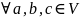
2.'
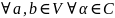
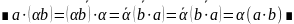
Замечание. Свойства 1 и 2, 1' и 2' показывают, что скалярное произведение на V является эрмитовой полуторалинейной формой. А свойство 3 показывает, что порождённая ею эрмитова квадратичная форма является положительно определённой.
Из свойств 1 и 2,4, 1' и 2' вытекает общее свойство полуторалинейности
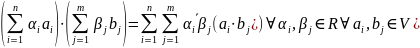
Примеры.
1.
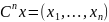
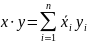
Определение. Комплексное линейное пространство, на котором задано скалярное произведение называется унитарным пространством.
Замечание. Всякое подпространство унитарного пространства также является унитарным относительно сужения скалярного произведения на него.
Теорема
Теорема. Всякое конечномерное действительное (комплексное) линейное пространство можно превратить в евклидово (унитарное) пространство.
V-действительное пространство - базис
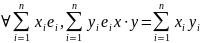Проверим, что все свойства выполняются
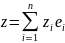
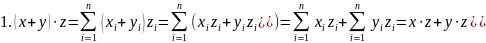
2.
Если
,
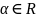то
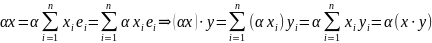
3.
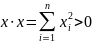Если не все
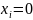
4.
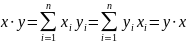
Если
V-комплексное пространство,
то аналогичным образом можно рассмотреть
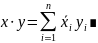
Гл 2 Пр2 Длина вектора и угол между векторами в евклидовом и унитарном пространствах
Длина вектора и неравенство Коши-Буняковского
Определение.
Длиной вектора а из евклидова (унитарного)
пространства называется число
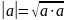Из свойства 3 определения скалярного
произведения такое определение корректно.
Замечание. Свойства длины вектора:
1.
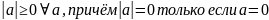
2.
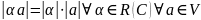
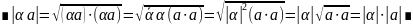
Теорема
(неравенство Коши-Буняковского).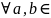
евклидова
(унитарного) пространства
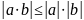(1).
Причём равенство имеет место только
тогда, когда векторы
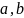линейно зависимы.
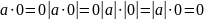
Пусть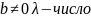
Рассмотрим
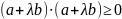(2)
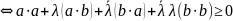
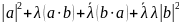
Пусть
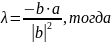
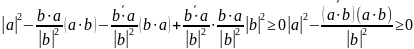
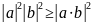
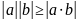
Если
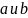линейно независимы, то
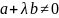значит (2) строгое, а значит и (1) строгое.
Если же
линейно зависимы, то
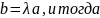
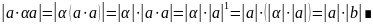
Угол между векторами. Неравенство треугольника
Пусть a,b
0
вект. евкл. пр-ва. Согласно нер-ву
Коши-Буняковского
⇒
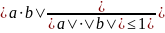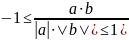
В силу этого
нер-ва существует угол ϕ
[0;π],
т.что cosϕ =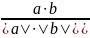
это угол ϕ наз. углом между векторами a
и b.
Теорема (неравенство треугольника).
евклидову (унитарному) пространсту
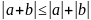
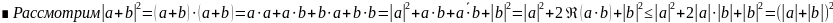Учитывая, что под квадратом стоят
положительные величины⇒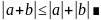
Гл 2 пр 3 Ортогональные векторы в евклидовых и унитарных пространствах
Ортогональные векторы и их свойства
Определение.
Векторы a и b
евклидова (унитарного) пространства
называются ортогональными, если
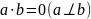
Свойства
1.
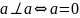т.е. в евклидовом (унитарном) пространствах
изотропным является только нулевой
вектор.
2. Вектор
ортогонален каждому вектору пространства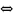
когда он нулевой.
3. Теорема(Пифагора)
Если вектор
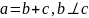
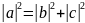
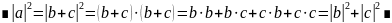
4.Если
вектор
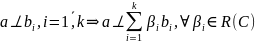
5. Совокупность попарно ортогональных ненулевых векторов линейно независима(было доказано ранее в более общем случае).
Ортогональное дополнение
Определение. U-подпространство евклидова (унитарного) пространства V. Множество всех векторов пространства V ортогональных каждому вектору U называется ортогональным дополнением к этому подпространству и обозначается U┴.
Теорема.
Для
подпространства
U конечномерного евклидова
(унитарного)пространства V
V=U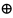
U┴
(было доказано ранее)
Следствие
1. Размерность
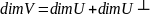
Следствие
2.
.
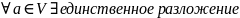
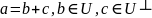При этом b
называют ортогональной проекцией
вектора a
на подпространство U,
а вектор c
называют ортогональной составляющей.
Процесс ортогонализации
Теорема.
Пусть
-
конечная система векторов евклидова
(унитарного) пространства. Тогда в этом
пространстве существует ортогональная
система векторов
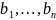эквивалентная исходной системе векторов.
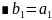а
далее по индукции
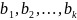уже построены, то
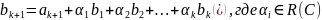
При условии, что он ортогонален предыдущим.
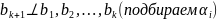
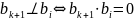
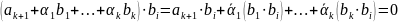
В силу
ортогональности
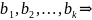
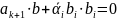
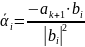
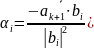
Остаётся
показать, что системы a и
b эквивалентны.
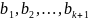
вектор линейно выражается через векторы верно и обратное.
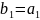Из
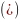видно,что
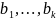выражаются через векторы
то и
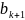выражается через векторы
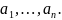Таким образом эти две системы векторов
эквивалентны.
Замечание. Процесс описанный в данном доказательстве называется процессом ортогонализации.
Следствие
3. Если система векторов
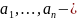линейно
независима, то и
- полученная из неё процессом ортогонализации
также линейно независима. (ранги
эквивалентных систем равны)
Следствие
4. Если
ортогональны,
то
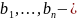в
точности совпадают с данной системой.
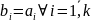то тогда в
все коэффициенты
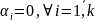
Действительно
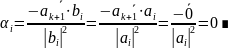
Ортонормированный базис евклидова (унитарного) пространства. Матрица Грама
Теорема. Всякая ортогональная система ненулевых векторов евклидова (унитарного) конечномерного пространства либо является базисом этого пространства, либо может быть дополнена до ортогонального базиса этого пространства.
Следствие. В ненулевом конечномерном евклидовом (унитарном) пространстве существует ортонормированный базис. (Любые 2 вектора ортогональны и длина каждого =1)
- получили процессом ортогонализации
Заменяем:
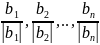ортогональность
не нарушается и кроме того, длина каждого
вектора этой системы =1.
Как и в случае
билинейных форм скалярное произведение
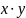может быть записано, как
,
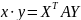где
-
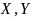столбцы координат векторов
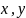в некотором базисе
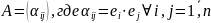
Такая матрица А называется матрицей Грама.
Если базис ортогональный, то матрица(Грама) А- диагональная.
А если
ещё и ортонормированный, то А=Е- единичная
и тогда
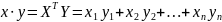
В случае
унитарного пространства
;
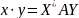если А=Е
