Глава 1

Гл1 Пр1 Линейные формы.

Определения и примеры

Определение. V-векторное пр-во над P.Линейной формой на V называется отображение f:V→P

f(x+y)=f(x)+f(y) для любых x,y из V

f(αx)=αf(x) для любых α из P

Примеры:

1. f(X)=0 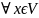– нулевая линейная форма

2. 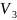-пр-во. свобод. Вектор 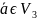-фиксированный вектор

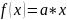
3.

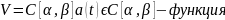
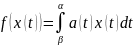
4.V- произвольное пр-во над P.

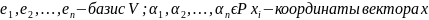
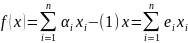
Всякую лин. ф. можно представить в таком виде.

V- линейное пр-во над P f:V→P-линейная форма на V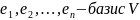

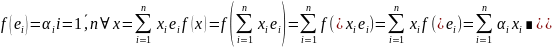
Таким образом из равенства (1) видно что линейная форма представляет собой многочлен 1-ой степени от нескольких перменных. 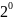Сопряженное пространство.

f:V→P-является частным случаем линейного оператора.

Определение. Мн-во всех линейных операторов f:V→P само образует векторное пр-во над P, которое наз. сопряженным пр-ву V и обозн V*.

Пространство V*изоморфно пространству строчек длинны n? И значит оно является n-мерным. Рассмотрим линейные формы

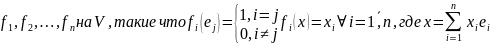
Покажем, что набор данных форм является линейно независимым.

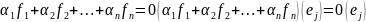
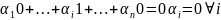
По определению, это означает, что набор линейных форм линейно независим. А поскольку таких форм соотв. размерности V* то они образуют базис, который явл. двойственным базису .

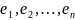Предложение

f:V→P-линейная 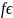V*

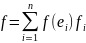
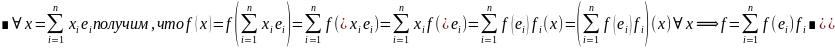
Гл 1 Пр2 Билинейные формы.

Определения и примеры

Определение. V – лин. Пр-во над P. Билинейной формой над P наз F:V*V→P

F(x+y,z)=F(x,z) +F(y,z)

F(αx,z)=αF(x,z)

F(x,y+z)=F(x,y)+F(x,z)

F(x,αz)=αF(x,z)

Если F(x,y)=F(y,x) ---наз. симметрической

Если F(x,y)=-F(y,x) – наз. кососимметрической.

Примеры:

1)F(x,y)=0 – нулевая.

2)F(x,y)=x*y

3)

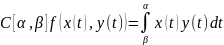
4) V- линейное пр-во над P

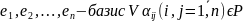
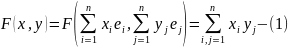
Пример 4) является общим в том, что всякую билинейную форму можно представит в виде (1).

V пр-во над P F-билинейная форма на V

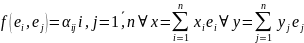
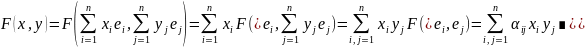
Матрица билинейной формы.

Коэф-ты в (1) образуют матр А=(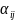 ) матрица билинейной формы А в базисе ;

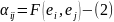Пусть X-столбец 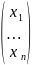где 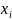коорд x в базисе .

Y-столбец 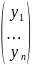где 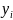коорд. y в базисе . Тогда матрица бил. ф-мы F(x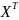,y)= AY

Придложения: F- билинейная форма на V и А-матрица А в некотором базисе.

1)F-симметр⇔A –симметр;

2)F-кососимметр⇔A-кососим

1. ⟹

Пусть А симметр. Докажем, что тогда её матрица симметрична

2. ⟸

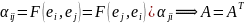
А симметр

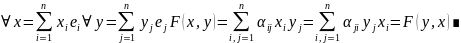
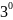Изменение матрицы билинейной формы при изменении базиса.

A=( )-матрица F в базисе 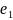, 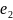… 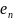; B=(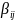 ) матрица F в базисе ;

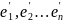S- матрица перехода от 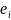к ;

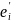X= , Y= в базис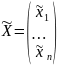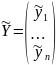е ; , в базисе ;

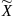тогда X=S ,Y=S ;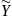

тогда F(x,y)= AY= ;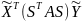

F(x,y)=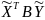 ;=>B=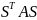 , причем S-невырожденная;

Умножение любой матрицы на невырожденную не меняет ранг матрицы. Ранг билинейной формы в любом базисе называется рангом билинейной формы. Если ранг совпадает с размерностью то форма называется невырожденной.

Гл1 Пр3 Квадратичные формы

10.Квадратичная форма и полярная билинейная форма.

Определение. F-билинейная форма V над P

ϕ: V→P такое, что ϕ(х)=F(x, x) для любого х ϵV называется квадратичной формой на V, порожденной билинейной формой F.

Пример:

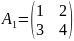1. F₁, F₂ ,

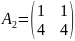
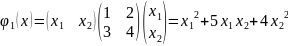
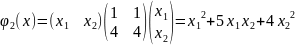
Видим, что ϕ₁=ϕ₂

Теорема 1. Для квадратичной формы на V над P, char p≠2, Ǝ! билинейная форма на этом пространстве порождающая ϕ.(Эта билинейная форма называется полярной билинейной)

Везде далее cчитаем что char p≠2

ϕ(х)=F(x, x),

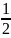F(x, y)= (ϕ(x+y)-ϕ(x)-ϕ(y)) (**)

F(x+y, x+y)=F(x, x)+F(x, y)+F(y, x)+F(y, y) ⇔ ϕ(x+y)=ϕ(x)+2 F(x, y)+ϕ(y)

F(x, y)= (ϕ(x+y)-ϕ(x)-ϕ(y))

Замечание. Если char p=2 то Ǝ! не выполняется.

Следствие. Согласно теореме существует биекция между множеством всех симметрических билинейных форм и множество всех квадратичных форм.