Cобственные векторы и собственные значения
Пусть A – матрица некоторого линейного преобразования порядка n. Определение. Многочлен n-ой степени
P()=det(A-Е) (1.1)
называется характеристическим многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы. Определение. Ненулевой вектор x линейного пространства V, удовлетворяющий условию
А(х)=х, (1.2)
называется собственным вектором преобразования A. Число называется собственным значением. Замечание. Если в пространстве V задан базис, то это условие можно переписать следующим образом:
Ах=х, (1.3)
где A – матрица преобразования, x – координатный столбец. Определение. Алгебраической кратностью собственного значения jназывается кратность корня j характеристического многочлена. Определение. Совокупность всех собственных значений называетсяспектром матрицы.
Алгоритм нахождения собственных значений и собственных векторов
Найти собственные значения матрицы:
записать характеристическое уравнение:
det(A-Е)=0; (1.4)
найти его корни j, j=1,...,n и их кратности.
Найти собственные векторы матрицы:
для каждого j решить уравнение
(A- jE)x=0; (1.5)
найденный вектор х и будет собственным вектором, отвечающим собственному значению j.
Пример1
Найдем собственные значения и собственные векторы, если известна матрица преобразования:
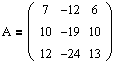
Записываем характеристический многочлен (1.1) и решаем характеристическое уравнение (1.4):
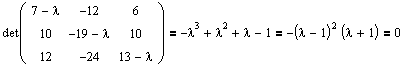
Получаем два собственных значения: 1=1 кратности m1=2 и 2=-1 кратности m2=1. Далее с помощью соотношения (1.5) находим собственные векторы. Сначала ищем ФСР для 1=1:
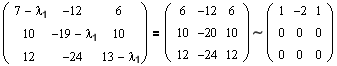
Очевидно, что rang=1, следовательно, число собственных векторов для 1=1 равно n-rang=2. Найдем их:
Аналогичным образом находим собственные векторы для 2=-1. В данном случае будет один вектор:
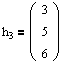
21
Приведение квадратичной формы к каноническому виду.
Определение
10.4. Каноническим
видом квадратичной
формы (10.1) называется следующий
вид: 
. (10.4)
Покажем, что в базисе из собственных векторов квадратичная форма (10.1) примет канонический вид. Пусть
-
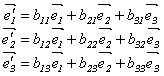нормированные собственные векторы,
соответствующие собственным
числам λ1,λ2,λ3 матрицы
(10.3) в ортонормированном базисе 
.
Тогда матрицей перехода от старого
базиса к новому будет
матрица
.
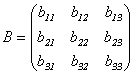В новом базисе матрица А примет
диагональный вид (9.7) (по свойству
собственных векторов). Таким образом,
преобразовав координаты по формулам:
,
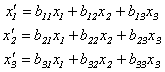получим в новом базисе канонический вид квадратичной формы с коэффициентами, равными собственным числам λ1, λ2, λ3:
. (10.5)
Замечание 1. С геометрической точки зрения рассмотренное преобразование координат представляет собой поворот координатной системы, совмещающий старые оси координат с новыми.
Замечание 2. Если какие-либо собственные числа матрицы (10.3) совпадают, к соответствующим им ортонормированным собственным векторам можно добавить единичный вектор, ортогональный каждому из них, и построить таким образом базис, в котором квадратичная форма примет канонический вид.
Пример.
Приведем к каноническому виду квадратичную форму
x² + 5y² + z² + 2xy + 6xz + 2yz.
Ее
матрица имеет вид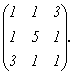 
В примере,
рассмотренном в лекции 9, найдены
собственные числа и ортонормированные
собственные векторы этой матрицы:
Составим
матрицу перехода к базису из этих
векторов:
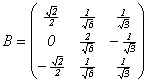(порядок
векторов изменен, чтобы они образовали
правую тройку). Преобразуем координаты
по формулам:
.
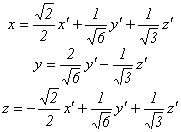
Получим:
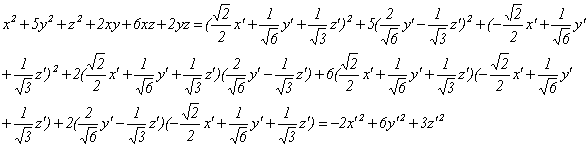
Итак, квадратичная форма приведена к каноническому виду с коэффициентами, равными собственным числам матрицы квадратичной формы.