- •2.1.1. Сложение векторов
- •2.1.2 Вычитание векторов
- •2.1.3. Умножение вектора на число
- •Приложение:
- •Свойства векторного произведения.
- •Геометрический смысл смешанного произведения
- •Свойства смешанного произведения:
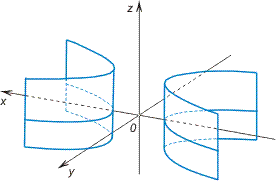
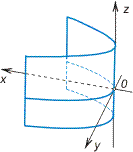
- •Чертеж фигуры эллипс
- •Уравнения поверхностей второго порядка
- •Преобразование общего уравнения прямой линии к каноническому и параметрическому виду
- •Cобственные векторы и собственные значения
- •Алгоритм нахождения собственных значений и собственных векторов
- •Пример1
Уравнения поверхностей второго порядка
|
|
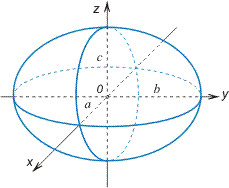
Эллипсоид
a, b, c — полуоси
|
|
|
|
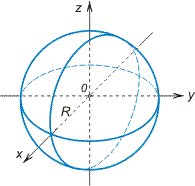
Сфера (частный случай эллипсоида)
|
|
|
|
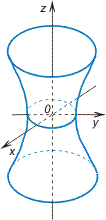
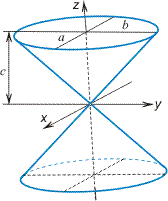
Однополостный гиперболоид
c — действительная полуось, a и b — мнимые полуоси |
|
|
|
Двуполостный гиперболоид
c — действительная полуось, a и b — мнимые полуоси |
|
|
|
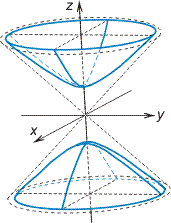
Конус
Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат
|
|
|
|
|
|
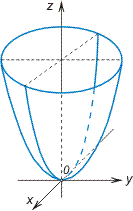
Эллиптический параболоид
|
|
|
|
|
|
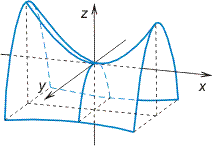
Гиперболический параболоид
|
|
|
|
|
|
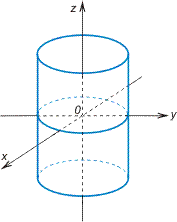
Эллиптический цилиндр
a и b — полуоси |
|
|
|
|
|
Гиперболический цилиндр
|
|
|
|
Параболический цилиндр
p — фокальный параметр |
|
16
Преобразование общего уравнения прямой линии к каноническому и параметрическому виду
Преобразовать прямую линию
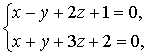
заданной в общем виде, к канонической и параметрической форме. Для этого необходимо найти какую – нибудь точку, через которую проходит прямая линия (опорную точку). Пусть эта точка имеет координату (х, у, 0). Координаты этой точки должны удовлетворять уравнению прямой, и система примет вид
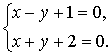
Эта система имеет решение
![]() .
.
Итак, опорная точка имеет координаты
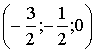 .
.
Найдём направляющий вектор прямой как векторное произведение нормальных векторов плоскостей:
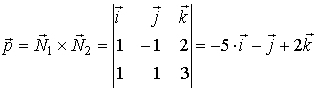 .
.
Каноническое
уравнение прямой имеет вид 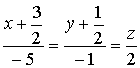 .
Если обозначить общее значение этих
дробей величиной t,
.
Если обозначить общее значение этих
дробей величиной t,
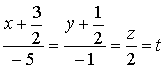
то
рассматривая каждое равенство в
отдельности 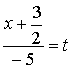 ,
, 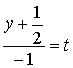 ,
, ![]() ,
получим уравнение прямой линии в
параметрической форме
,
получим уравнение прямой линии в
параметрической форме
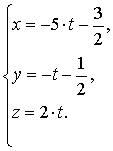
17
Линейными операциями называются операции сложения матриц и умножение матрицы на число.
Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый
элемент которой равен сумме соответствующих элементов слагаемых:
![]() .
.
 ,
, 
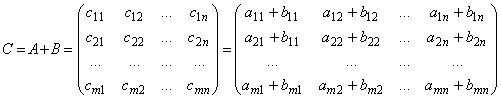
Произведением матрицы на число называется матрица той же размерности, каждый элемент которой
равен произведению соответствующего элемента на число:
![]() .
.
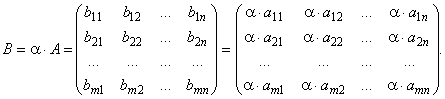
Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Пример 1. Составить транспонированную матрицу, полученную из А:
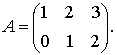
Решение: Поменяем местами строки и столбцы, сохраняя порядок:
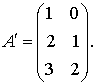
18
Начнем с
самого ужасного и непонятного.
Рассмотрим квадратную матрицу ![]() . Обратную
матрицу
. Обратную
матрицу ![]() можно
найти по следующей формуле:
можно
найти по следующей формуле:
![]() ,
где
,
где ![]() –
определитель матрицы
,
–
определитель матрицы
, ![]() –
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения:
Как Вы уже, наверное, заметили, обратная
матрица обозначается надстрочным
индексом ![]()
Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.
Пример:
Найти обратную
матрицу для матрицы ![]()
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
![]()
Если с пониманием сего действа плоховато, ознакомьтесь с материалом Как вычислить определитель? Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом
примере, как выяснилось, ![]() ,
а значит, всё в порядке.
,
а значит, всё в порядке.
2) Находим
матрицу миноров ![]() .
.
Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.
Матрица
миноров имеет такие же размеры, как и
матрица
,
то есть в данном случае ![]() .
Дело
за малым, осталось найти четыре числа
и поставить их вместо звездочек.
.
Дело
за малым, осталось найти четыре числа
и поставить их вместо звездочек.
Возвращаемся
к нашей матрице
Сначала
рассмотрим левый верхний элемент:
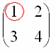 Как
найти его минор?
А
делается это так: МЫСЛЕННО вычеркиваем
строку и столбец, в котором находится
данный элемент:
Как
найти его минор?
А
делается это так: МЫСЛЕННО вычеркиваем
строку и столбец, в котором находится
данный элемент:
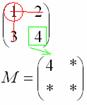
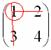 Оставшееся
число и является минором
данного элемента,
которое записываем в нашу матрицу
миноров:
Оставшееся
число и является минором
данного элемента,
которое записываем в нашу матрицу
миноров:
 Рассматриваем
следующий элемент матрицы
:
Рассматриваем
следующий элемент матрицы
:
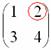 Мысленно
вычеркиваем строку и столбец, в котором
стоит данный элемент:
Мысленно
вычеркиваем строку и столбец, в котором
стоит данный элемент:
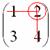 То,
что осталось, и есть минор данного
элемента, который записываем в нашу
матрицу:
То,
что осталось, и есть минор данного
элемента, который записываем в нашу
матрицу:
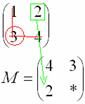
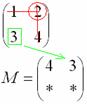 Аналогично
рассматриваем элементы второй строки
и находим их миноры:
Аналогично
рассматриваем элементы второй строки
и находим их миноры:
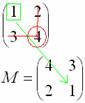 Готово.
Готово.
![]() –
матрица миноров
соответствующих элементов матрицы
.
–
матрица миноров
соответствующих элементов матрицы
.
3) Находим
матрицу алгебраических дополнений ![]() .
.
Это просто.
В матрице миноров нужно ПОМЕНЯТЬ
ЗНАКИ у
двух чисел:
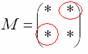 Именно
у этих чисел, которые я обвел в кружок!
Именно
у этих чисел, которые я обвел в кружок!
![]() –
матрица алгебраических
дополнений соответствующих элементов
матрицы
.
–
матрица алгебраических
дополнений соответствующих элементов
матрицы
.
И всего-то лишь…
4) Находим транспонированную матрицу алгебраических дополнений .
Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.
![]() –
транспонированная матрица
алгебраических дополнений соответствующих
элементов матрицы
.
–
транспонированная матрица
алгебраических дополнений соответствующих
элементов матрицы
.
5) Ответ.
Вспоминаем нашу формулу Всё найдено!
Таким образом,
обратная матрица:
![]()
Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статьеДействия с матрицами.
Как проверить решение?
Необходимо
выполнить матричное умножение ![]() либо
либо ![]()
Проверка:
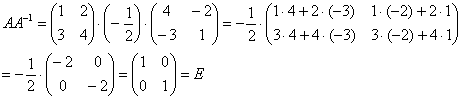
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно, более подробную информацию можно найти в статье Свойства операций над матрицами. Матричные выражения. Также заметьте, что в ходе проверки константа (дробь) выносится вперёд и обрабатывается в самом конце – после матричного умножения. Это стандартный приём.
Переходим к более распространенному на практике случаю – матрице «три на три».
Пример:
Найти обратную
матрицу для матрицы 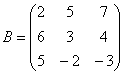
Алгоритм точно такой же, как и для случая «два на два».
Обратную
матрицу найдем по формуле: ![]() ,
где
,
где ![]() –
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы ![]() .
.
1) Находим определитель матрицы.
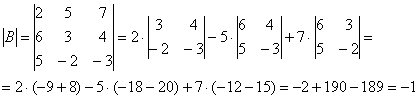 Здесь
определитель раскрыт по
первой строке.
Здесь
определитель раскрыт по
первой строке.
Также не
забываем, что ![]() ,
а значит, всё нормально – обратная
матрица существует.
,
а значит, всё нормально – обратная
матрица существует.
2) Находим матрицу миноров .
Матрица
миноров имеет размерность «три на
три»  ,
и нам нужно найти девять чисел.
,
и нам нужно найти девять чисел.
Я подробно рассмотрю парочку миноров:
Рассмотрим
следующий элемент матрицы:
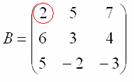 МЫСЛЕННО
вычеркиваем строку и столбец, в котором
находится данный элемент:
МЫСЛЕННО
вычеркиваем строку и столбец, в котором
находится данный элемент:
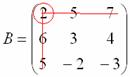
Оставшиеся
четыре числа записываем в определитель
«два на два»
 Этот
определитель «два на два» и является
минором данного элемента.
Его нужно вычислить:
Этот
определитель «два на два» и является
минором данного элемента.
Его нужно вычислить:
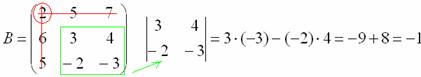 Всё,
минор найден, записываем его в нашу
матрицу миноров:
Всё,
минор найден, записываем его в нашу
матрицу миноров:
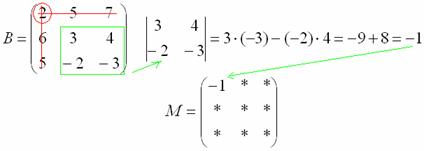
Как Вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.
Ну и для
закрепления – нахождение еще одного
минора в картинках:
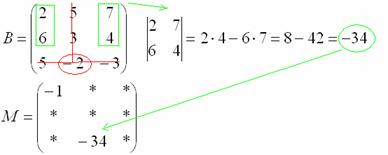 Остальные
миноры попробуйте вычислить самостоятельно.
Остальные
миноры попробуйте вычислить самостоятельно.
Окончательный
результат:
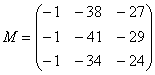 –
матрица миноров соответствующих
элементов матрицы
.
–
матрица миноров соответствующих
элементов матрицы
.
То, что все миноры получились отрицательными – чистая случайность.
3) Находим
матрицу алгебраических дополнений ![]() .
.
В матрице
миноров необходимо СМЕНИТЬ
ЗНАКИ строго
у следующих элементов:
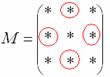 В
данном случае:
В
данном случае:
 –
матрица алгебраических дополнений
соответствующих элементов матрицы
.
–
матрица алгебраических дополнений
соответствующих элементов матрицы
.
4) Находим транспонированную матрицу алгебраических дополнений .
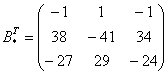 –
транспонированная матрица
алгебраических дополнений соответствующих
элементов матрицы
.
–
транспонированная матрица
алгебраических дополнений соответствующих
элементов матрицы
.
5) Ответ:
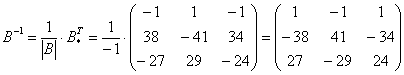
Проверка:
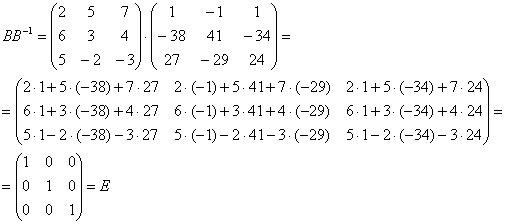
Таким образом, обратная матрица найдена правильно.
19
Пусть ![]() — квадратная
матрица порядка
— квадратная
матрица порядка ![]() с
коэффициентами из кольца
с
коэффициентами из кольца ![]() ,
, 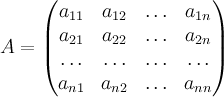 .
.
Определение
1. Определителем1) ![]() матрицы
называется
алгебраическая сумма всевозможных
произведений коэффициентов
матрицы
называется
алгебраическая сумма всевозможных
произведений коэффициентов ![]() ,
взятых по одному из каждой строки и
каждого столбца. Иначе говоря,
,
взятых по одному из каждой строки и
каждого столбца. Иначе говоря,
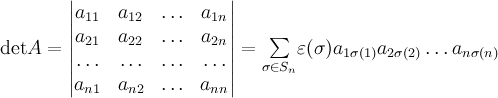 ,
,
где
суммирование ведется по
всем подстановкам порядка
, ![]() — знак
подстановки
— знак
подстановки ![]() .
.
Замечание. Часто определитель матрицы определяют рекурсивно, используя разложение по первой строке (частный случай теоремы Лапласа).
Пример
1. Определитель матрицы порядка
2: 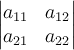 равен
равен ![]() .
.
Пример 2. Определитель матрицы порядка 3 вычисляется по формуле
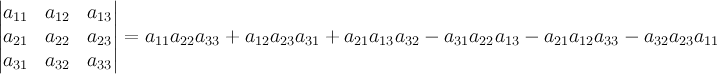 .
.
При
вычислении определителей третьего
порядка полезно помнить так называемое
«правило треугольника»: произведение
элементов, соединенных линиями, на
первой диаграмме берется со знаком
«+»
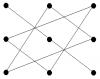 произведение
элементов, соединенных линиями, на
второй диаграмме берется со знаком «-»
произведение
элементов, соединенных линиями, на
второй диаграмме берется со знаком «-»
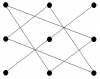
Свойства определителя
Предложение1. Определитель квадратной матрицы
и определитель транспонированной к
ней матрицы ![]() совпадают:
совпадают: ![]() .
.
Предолжение 2. Если в определителе матрицы поменять местами любые две строки, то он изменит знак на противоположный.
Предложение 3. Справедливы следующие свойства:
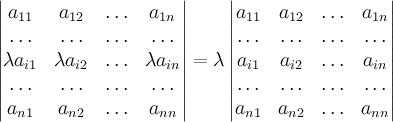 ,
, .
.
Предложение 4. Определитель с нулевой строкой равен нулю.
Предложение
5. Если
в квадратной матрице
две
строки совпадают, то ![]() .
.
Предложение 6. Определитель не меняется, если к некоторой его строке прибавить другую строку, умноженную на ненулевой скаляр.
Предложение7. Пусть 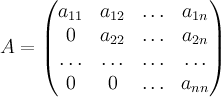 — верхнетреугольная
матрица порядка
,
тогда
— верхнетреугольная
матрица порядка
,
тогда ![]() .
.
Предложение8. Пусть
и ![]() квадратные матрицы порядка
.
Тогда
квадратные матрицы порядка
.
Тогда ![]() .
.
20