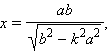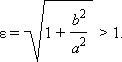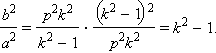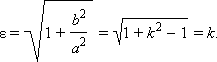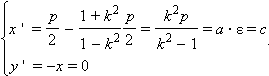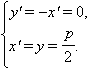Чертеж фигуры эллипс

F₁ , F₂ – фокусы . F₁ = ( c ; 0); F ₂ (- c ; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

12

Гиперболой ( рис.1 ) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек  F₁ и F₂ , называемых фокусами гиперболы, есть величина постоянная.

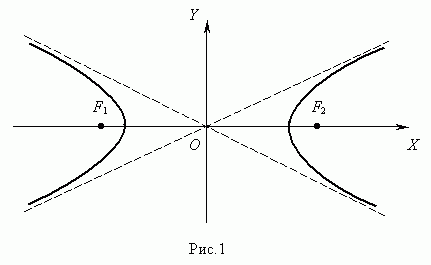
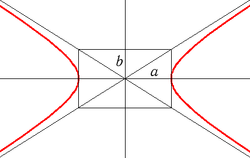
Уравнение гиперболы ( рис.1 ) :

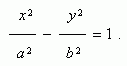
Число a называется действительной полуосью гиперболы, число b – мнимой полуосью.

Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.

Отрезок  F₁F₂ = 2 с ,  где   , называется фокусным расстоянием. Отрезок  AB = 2 a называется  действительной осью гиперболы, а отрезок  CD = 2 b –  мнимой осью гиперболы. Число  e = c / a ,  e > 1 называется эксцентриситетом гиперболы. Прямые   y =  ( b / a ) x называются асимптотами гиперболы.

 

Пусть  Р ( х₁ ,  у ₁ ) – точка гиперболы, тогда  уравнение касательной к гиперболе в данной точке имеет вид:

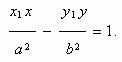
Условие касания прямой  y = m x + k  и гиперболы  х ² / a ²  –  у  ² / b ²  = 1 :

 

 

k ²  = m ² a ² – b ² .

Свойство 10.6. 

Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы.

Доказательство

Отрезок AB называется действительной осью гиперболы, его длина равна 2a. Число a называется действительной полуосью гиперболы, число b – мнимой полуосью.

Свойство 10.7. 

Гипербола имеет две взаимно перпендикулярные оси симметрии.

Доказательство

Свойство 10.8. 

Гипербола имеет центр симметрии.

Доказательство

Центр симметрии гиперболы называют центром гиперболы.

Свойство 10.9. 

Гипербола пересекается с прямой y = kx при   в двух точках. Если 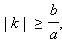  то общих точек у прямой и гиперболы нет.

Доказательство

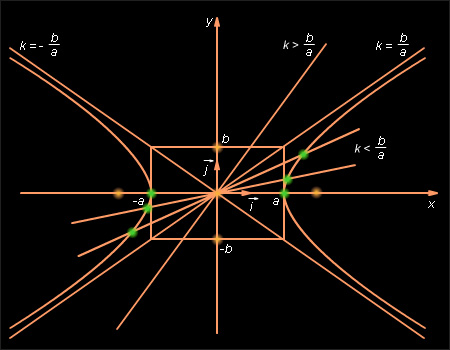
Так как гипербола симметрична относительно осей координат, то достаточно изучить ее форму в первом квадранте координатной плоскости. Из полученных формул 

видно, что при возрастании k от нуля до   (при этом угол наклона прямой к оси Ox возрастает от нуля до некоторого значения) и абциссы, и ординаты точек пересечения прямой с гиперболой возрастают. Прямая y = kx пересекает гиперболу во все более далеких от начала координат точках. Таким образом, гипербола имеет вид, изображенный на рис. 10.9.1, и состоит из двух не связанных между собой частей, называемых ее ветвями.

Рисунок 10.9.1

Точки   и   называются фокусами гиперболы. Здесь 

Величина   называется эксцентриситетом гиперболы и обозначается так же, как и в случае эллипса, буквой ε.

Из определения 

Из формулы видно, что чем меньше эксцентриситет, тем более гипербола сжата к оси Ox.

В соответствии с обозначениями 

Тогда, аналогично случаю с эллипсом, 

Координаты точки A при переходе в новую систему координат будут равны 

То есть точка A в новой системе координат имеет те же координаты, что и фокус   гиперболы, и поэтому совпадает с ним.

Уравнение же прямой l в новой системе координат будет иметь вид 

Обозначим 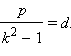  Так как    то, поскольку для гиперболы ε > 1, имеем d < a. Прямая x = d называется директрисой гиперболы, соответствующей фокусу    Прямую x = –d называют директрисой, соответствующей фокусу 

С учетом симметрии гиперболы относительно осей координат, свойство, с помощью которого определили гиперболу, в новых терминах можно сформулировать так же, как и в случае эллипса: отношение расстояния от любой точки гиперболы до одного из его фокусов к расстоянию от этой точки до соответствующей ему директрисы есть величина постоянная и равная эксцентриситету. Вид гиперболы и ее директрис в канонической системе координат приведен на рис. 10.9.2.

13

Парабола – множество всех точек плоскости, каждая из которых одинаково

удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой

называется параметром параболы и обозначается через р>0.

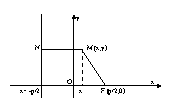Пусть M(x;y) – произвольная

точка M с F. Проведем отрезок

MN перпендикулярно

директрисе. Согласно

определению MF=MN.

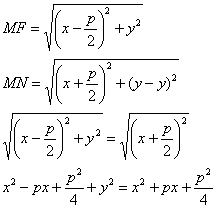
Свойство 10.10. 

Парабола имеет ось симметрии.

Доказательство

Ось симметрии называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Вершина параболы в канонической системе координат находится в начале координат.

Свойство 10.11. 

Парабола расположена в полуплоскости x ≥ 0.

Доказательство

При замене системы координат заданная в условии точка A с координатами   будет иметь новые координаты, определяемые из соотношений 

Таким образом, точка A будет иметь в канонической системе координаты   Данную точку   называют фокусом параболы и обозначают буквой F.

Прямая l, задаваемая в старой системе координат уравнением 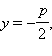  в новой системе координат будет иметь вид   или, опуская штриховку, 

Данная прямая в канонической системе координат называется директрисой параболы. Расстояние от нее до фокуса называется фокальным параметром параболы. Очевидно, он равен p. Эксцентриситет параболы по определению полагают равным единице, то есть ε = k = 1.

Теперь свойство, через которое мы определили параболу, в новых терминах можно сформулировать следующим образом: любая точка параболы равноудалена от ее фокуса и директрисы.

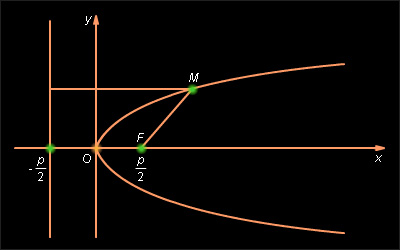
Вид параболы в канонической системе координат и расположение ее директрисы приведены на рис. 10.10.1.

Рисунок 10.10.1

14

Рассмотрим ряд преобразований, связанных с переходом из одной системы координат в другую. Здесь ( х,  у ) и ( х',  у' ) - координаты произвольной точки Р соответственно в старой и новой системе координат.

 

Параллельный перенос. Передвинем систему координат XОY в плоскости так, чтобы оси OX и OY оставались параллельны самим себе, а начало координат О сместилось в точку О' ( a, b ). Получим новую систему координат X'O'Y' ( рис.1 ):

Координаты точки  Р  в новой и старой системе координат связаны соотношениями:

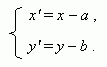
Поворот вокруг начала координат. Повернём систему координат XОY в плоскости на угол   ( рис.2 ).

Теперь координаты точки  Р  в новой и старой системе координат связаны соотношениями:

В частном случае    =    получим центральную симметрию относительно начала координат О :

 

15