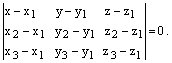Приложение:

4

Свойства векторного произведения.

Справедливы свойства

,                                                                (6)

,                                                          (7)

,                                                (8)

где  ,  ,   - произвольные векторы,   - скаляр.

5

Смешанным произведением трех векторов  ,  ,   называется число, равное скалярному произведению вектора   на вектор  : 

Геометрический смысл смешанного произведения

Геометрический смысл смешанного произведения: если тройка векторов   правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:  . В случае левой тройки   смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:  . Если  ,   и   компланарны, то их смешанное произведение равно нулю.

Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах  ,   и   равен модулю смешанного произведения этих векторов:

Объем пирамиды, построенной на этой тройке векторов равен

Свойства смешанного произведения:

1°    

2°    

3°    Три вектора компланарны тогда и только тогда, когда 

4°    Тройка векторов является правой тогда и только тогда, когда  . Если же  , то векторы  ,   и  образуют левую тройку векторов.

5°    

6°    

7°    

8°    

9°    

10°    Тождество Якоби: 

Координаты:

Если векторы  ,   и   заданы своими координатами, то их смешанное произведение вычисляется по формуле

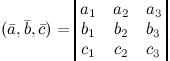
6

Сложение и вычитание векторов через координаты.

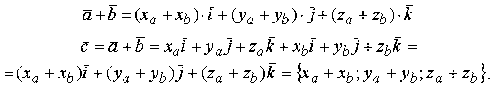
Координатный метод в билетах 3,4!!!!

7

Пусть М_о(х_о, у_о, z_о) – заданная точка в плоскости ,   = (А; В; С) – вектор, перпендикулярный плоскости , его называют нормальным вектором плоскости, и пусть М(х, у, z) – произвольная точка плоскости (рис. 43). Тогда     то есть

(2.28)

 

(2.28) – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

 

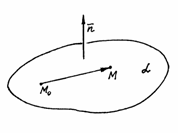
Рис. 43

Раскрыв скобки и сгруппировав слагаемые, получим   Обозначим    уравнение примет вид

 

(2.29)

 

(2.29) – общее уравнение плоскости.

Если в этом уравнении А, В, С, Д  0, то его можно привести к виду

 

(2.30)

 

(2.30) – уравнение плоскости в отрезках (аналогично (2.14)). Здесь а, в, с – отрезки, отсекаемые плоскостью на осях координат.

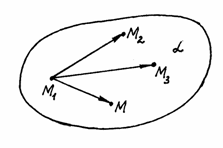
Пусть заданы три точки в плоскости: М₁(х₁, у₁, z₁), М₂(х₂, у₂, z₂), М₃(х₃, у₃, z₃), и пусть М(х, у, z) – произвольная точка плоскости (рис.44). Тогда       Эти векторы компланарны (лежат в одной плоскости), следовательно, их смешанное произведение равно нулю:  или через координаты

 

(2.31)

 

(2.31) – уравнение плоскости, проходящей через три данные точки.

 

 Возможны два случая взаимного расположения двух плоскостей в пространстве:

• Параллельны

• Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в  противном случаи они пересекаются.

Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство:

Пусть  и - данные плоскости, а1 и а2 - прямые в плоскости , пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в

плоскости . Допустим, что плоскости  и  не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости , и поэтому они не

пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости  через точку А проходят две прямые (а1 и а2) , параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД.

Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема2: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство:

Пусть  - плоскость, в -перпендикулярная ей прямая,  - плоскость, проходящая через прямую в, с - прямая, по которой пересекаются плоскости  и . Докажем, что плоскости  и  перпендикулярны. Проведем в плоскости  через точку пересечения прямой в с плоскостью  прямую а,

перпендикулярную прямой с. Проведем через прямые а и в плоскость . Она перпендикулярна прямой с, т.к. прямая с перпендикулярна прямым а и в. Т. к. прямые а и в перпендикулярны, то плоскости  и  перпендикулярны. ч.т.д.

8

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;              (3.2)

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

= ;                                       (3.3)

3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

.                                        (3.4)

Уравнения (3.4) называются каноническими уравнениями прямой.

Если две прямые l₁ и l₂ лежат на плоскости, то возможны три различных случая их взаимного расположения: 1)пересекаются (т.е. имеют одну общую точку); 2) параллельны и не совпадают; 3) совпадают.

Выясним, как узнать, какой из этих случаев имеет место, если эти прямые заданы своими уравнениями в общем виде:

 (12)

Если прямые l₁ и l₂ пересекаются в некоторой точке М(х,у), то координаты этой точки должны удовлетворять обоим уравнениям системы (12).

Следовательно, чтобы найти координаты точки пересечения прямых l₁ и l₂, надо решить систему уравнений (12):  1) если система (12) имеет единственное решение, то прямые l₁ и l₂ пересекаются;  2) если система (12) не имеет решения, то прямые l₁ и l₂ параллельны;  3) если система (12) имеет множество решений, то прямые l₁ и l₂ совпадают.

Условием совпадения двух прямых является пропорциональность соответствующих коэффициентов их уравнений.

9

приведения общего уравнения прямой   к каноническому уравнению прямой вида  .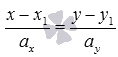

Если  , то переносим слагаемое   в правую часть равенства   с противоположным знаком  . В левой части равенства выносим А за скобки 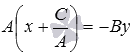 . Полученное равенство можно записать как пропорцию вида  .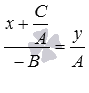

Если  , то оставляем в левой части общего уравнения прямой   только слагаемое  , а остальные переносим в правую часть с противоположным знаком:  . Теперь выносим в правой части равенства –B за скобки 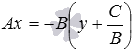  и записываем полученное равенство в виде пропорции 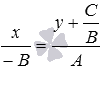 . Вот и все.

Запоминать полученные формулы не имеет смысла, проще повторять указанные действия при приведении общего уравнения прямой к каноническому виду.

10

11

Каноническое уравнение эллипса

 Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, назы­ваемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

О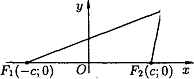 бозначим фокусы через   и  ,расстояние между ними через 2с, а сумму расстояний от произ­вольной точки эллипса до фокусов  — через 2а 

 Рис.27 (см. рис. 27). По определению 2а > 2с, т.е. a > с.

 Для вывода уравнения эллипса выберем систему координат Оху так, чтобы фокусы    и   лежали на оси Ох, а начало координат совпадало с серединой отрезка  . Тогда фокусы будут иметь следующие координаты:

и  .

 Пусть М(х;у) — произвольная точка эллипса. Тогда, согласно опре­делению эллипса,  , т. е.

 

Это, по сути, и есть уравнение эллипса.

Преобразуем уравнение (11.5) к более простому виду следующим образом:

Так как a > с, то  . Положим

   

Тогда последнее уравнение примет вид  или

   

Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса. Эллипс — кривая второго порядка.