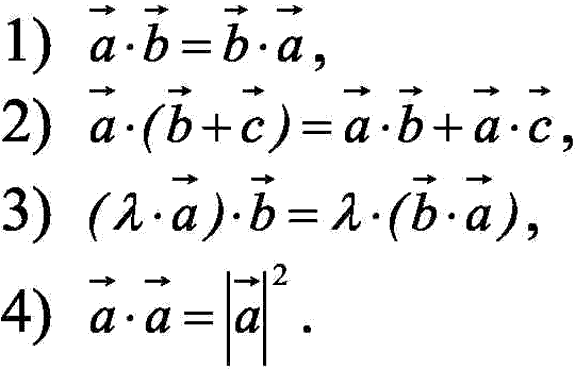1

Одна точка такого отрезка является началом, а другая граничная тока — концом вектор. Вектор обозначается  или  , где  является началом вектора, а — концом. Длина вектора (также называемый его модулем) обозначается как или  .

Нуль-вектором именуется вектор, в котором конец совпадает с его началом.

 

Рис. 2.1

О: Коллинеарными именуются векторы, которые расположены на параллельных (к примеру, на одной) прямых, а компланарными называются векторы, которые находятся в параллельных плоскостях.

О: Равными являются векторы, которые: 1) коллинеарны; 2) направлены одинаково ( то есть сонаправлены — ↑↑); 3) обладают равными модулями.

Таким образом, существует возможность переноса вектора параллельно самому себе, при перемещении начала в любую прочую точку. Векторы подобного типа именуются свободными.

Линейные операции, выполняемые над векторами: сложение, вычитание и умножение на число.

2.1.1. Сложение векторов

Суммой и совмещён с началом вектора с концом вектора (рис. 2.2, а).

Рис. 2.2

 

Свойства сложения векторов:

1⁰. Переместительный закон (коммутативность):

Доказательство выводится из рисунка 2.2, б. На этом же рисунке показано правило параллелограмма при сложении векторов и будет вектор, который совпадает с диагональю параллелограмма, берущей начало из общего начала векторов.

2⁰. Сочетательный закон:

Доказательство выводится из рис. 2.3. На этом же рисунке дано правило сложения нескольких векторов, в случае когда начало следующего вектора совмещается с концом предыдущего. Сумма представляет собой вектор, который соединяет начало первого вектора с концом последнего слагаемого вектора.

 

Рис. 2.3

2.1.2 Вычитание векторов

Разностью и векторов и является вектор , для которого справедливо . Исходя из определения имеем правило построения вектора , когда начала обоих векторов совмещены: необходимо совместить конец вычитаемого вектора с концом уменьшаемого вектора (рис 2.4).

Рис. 2.4

 

2.1.3. Умножение вектора на число

Произведением вектора на число  и направлен в ту же сторону если ( ) и противоположную сторону если ( ) .

Свойства умножения вектора на число:

1⁰. Сочетательное свойство (ассоциативность):

.

2⁰. Распределительное свойство (дистрибутивность):

Свойства легко проверяются геометрически.

Набор векторов   называется системой векторов.

Система из   векторов   называется линейно зависимой, если существуют такие числа  , не все равные нулю одновременно, что

(1.1)

Система из   векторов   называется линейно независимой, если равенство (1.1) возможно только при  , т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.

Замечания 1.2

1. Один вектор   тоже образует систему: при   — линейно зависимую, а при   — линейно независимую.

2. Любая часть системы векторов называется подсистемой.

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора  , то она линейно зависима.

4. Система из   векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов   линейно независима, а после присоединения к ней вектора   оказывается линейно зависимой, то вектор   можно разложить по векторам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

2

Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OA_x: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.

Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).

Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Единичный вектор, направленный вдоль оси x, обозначается i . Единичный вектор, направленный вдоль оси y, обозначается j . Единичный вектор, направленный вдоль оси z, обозначается k . Вектора i , j , k  называются координатными векторами. Любой вектор a  можно разложить по координатным векторам: a =x i +y j +z k. Коэффициенты разложения определяются единственным образом и называются координатами вектора a  в данной системе координат.

3

Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.

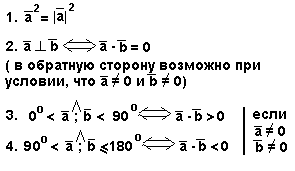
Свойства: