8. Расчет прочности по нормальному сечению центрально растянутых элементов
9. Расчет прочности по нормальному сечению изгибаемых элементов прямоугольного профиля с одиночной арматурой
10. Расчет прочности по нормальному сечению изгибаемых элементов прямоугольного профиля с двойной арматурой
Двойным называется армированием, когда помимо продольной рабочей арматуры в растянутой зоне вводится расчетная сжатая арматура в сжатой зоне бетона. Это бывает при ограниченных размерах знакопеременных моментов, невозможности увеличить класс бетона. Т. к. арматура одинаково хорошо работает и на растяжение и на сжатие, то введение небольшого количества арматуры в сжатую зону бетона позволяет существенно уменьшить размеры сечения.
RSС AS’ – расчетное усилие воспринимаемое арматурой в сжатой зоне. Тогда для элементов с двойным армированием RS AS = RSС AS’ + RB bх (принцип Лолейта ).
Основное положение прочности также как для элементов с одиночным армированием состоит в том, чтобы внешний изгибающий момент не превысил несущей способности. М ≤ (Мсеч.) = RB bх ٠(h0 - х / 2) + RSС AS’(h0 – а’)
Подбор сечений. Обычно необходимость двойного армирования приводит к решению задачи 1 типа: Известно: МРАСЧ. , b x h , В-, А-
Определить: АS и АS’
Решение: 1) RS ; RB ; RSС ; h0 = h – 3c – d /2. 2) А0 = М / RB b’f h02 При невозможности увеличить размеры и класс бетона необходимо двойное армирование. Для определения АS и АS’ используем условие 1и 2 принимая х = ξR h0 А0 = А0R находим АS’= (М - RB b ξR h0 ) / RSС (h0 – d) и принимаем по сортаменту необходимое количество стержней. Из условия 2 находим АS = (RSС AS’ / RS) + RB / RS b ξR h0 = АS’ + RB / RS b ξR h0 принимаем по сортаменту необходимое количество стержней в растянутой зоне.
Проверка несущей способности. При ней, когда все данные известны включая АS и АS’ : 1) из условия 2 находим фактическую высоту сжатой зоны х = (RS AS - RSС AS’) / RB b х ≤ ξR h0 2) зная значение х подставляем в условие 1 , предварительно уточнив h0. В случаях, когда в сжатой зоне уже имеется известное количество арматуры AS’, при всех прочих известных исходных данных. Из условия 1 находим значение А0 = М - RSС AS’ (h0 – d) / RB b’f h02 ≤ А0R затем находим АS =( RSС / RS ) AS’ + RB / RS b ξR h0 принимаем по сортаменту необходимое количество стержней.
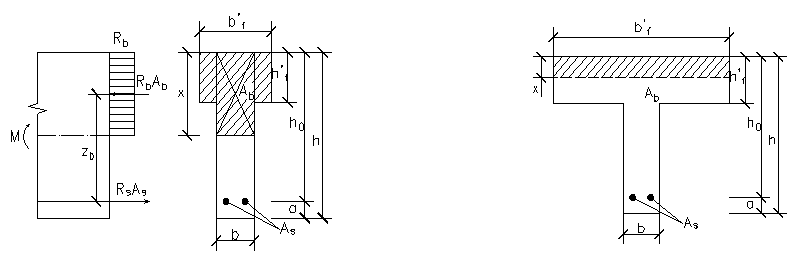
11. Расчет прочности по нормальному сечению изгибаемых элементов таврового профиля (граница сжатой зоны проходит в полке)
Балка, приводимая к тавровому сечению: при hf’≥0,1h, bсв=½c, bсв=1/6l; при hf’<0,1h, bсв=6hf’.
Балка таврового сечения: при hf’≥0,1h, bсв=6hf’, при 0,1h>hf’>0,05h, bсв=3hf’, при hf’<0,05h, bсв=0.
Граница сжатой зоны проходит в ребре:
RsAs=Rbbx+Rb(bf’-b)hf’↔ξRbbh0+Rb(bf’-b)hf’,
M≤Rbbx(h0-0,5x)+Rb(bf’-b)hf’(h0-0,5hf’)↔
αmRbbh02+Rb(bf’-b)hf’(h0-0,5hf’),
ξ≤ξR, Rs=σs, если ξ>ξR.
Граница сжатой зоны проходит в полке:
M≤Rbbf’hf’(h0-0,5hf’), RsAs=Rbbf’hf’, RsAs=Rbbf’x,
M=Rbbf’x(h0-0,5x)↔αmRbbf’h02,
M=RsAs(h0-0,5x)↔RsAsh0ς. Rs-расчетное сопротивление ар-ры растяжению, As-площадь сечения продольной ар-ры, Rb-расчетное сопротивление б. сжатию, Ab- площадь сжатой зоны б., h0-рабочая высота сечения, x-высота сжатой зоны б., b-ширина сечения, M-изгибающий момент, bf’ и hf’-ширина и высота полки таврового сечения в сжатой зоне.
ξR=ω/(1+(Rs/σsc,u)(1-ω/1,1))-граничная относительная высота сжатой зоны б., ξ=x/h0-относительная высота сжатой зоны б., σsc,u-предельное напряжение в арматуре сжатой зоны б., ω-характеристика сжатой зоны б.
