41. Переходные процессы в цепях с индуктивностью

Рассмотрим переходные процессы в цепи, у которой имеются две катушки с одинаковыми параметрами (для упрощения вычислений:  и  ) имеют индуктивную связь.

Вторая катушка замкнута накоротко, а первая подключается к источнику постоянного напряжения (рис. 9.19).

Рис. 9.19. Схема цепи со взаимной индуктивностью

Токи i₁ и i₂ связаны уравнениями:

, (9.28)

. (9.29)

В данном случае имеем нулевые начальные условия, т.е.

Установившиеся значения токов –

Приравняв нулю главный определитель, найдем корни характеристического уравнения:

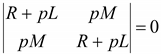, откуда 

При этом токи будут равны

, , (9.30)

. (9.31)Для нахождения постоянных интегрирования А₁ и А₂ находим 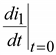 . Для этого умножим (9.28) на L, а (9.29) на М и вычтем его из первого уравнения при t = 0. Тогда

,

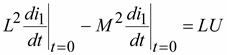Откуда ,

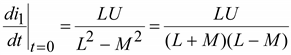При t = 0

;

.

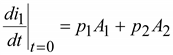Отсюда . Аналогично находим .

Тогда токи катушек будут равны

;

.

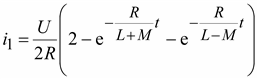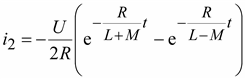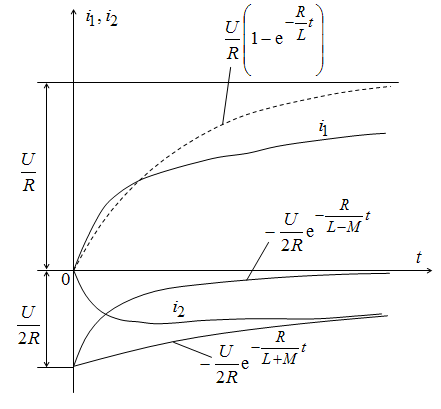
На рис. 9.20 построены кривые изменения токов i₁ и i₂. Одна из свободных составляющих затухает медленнее, т.е. имеет большую постоянную времени, определяемую суммой индуктивности L и взаимной индуктивности M, а вторая затухает быстрее, так как ее постоянная времени определяется разностью L – M. Для сравнения на рис. 9.20 показано, как изменялся бы ток первой катушки при ее включении, если бы вторая была разомкнута (штриховая линия).

Поскольку при включении токи катушек имеют противоположные направления, механические силы их взаимодействия стремятся оттолкнуть их друг от друга.

Получаемая от источника энергия преобразуется частично в тепло – джоулевы потери обеих катушек, а частично запасается в магнитном поле обеих катушек.

42. Переходные процессы в цепях, содержащих ёмкость

Переходные процессы в цепях первого порядка. Рассмотрим применение классического метода к расчету переходных процессов в цепях первого порядка. Это цепи, содержащие только однотипные реактивные элементы (емкости или индуктивности), процессы, в которых описываются дифференциальными уравнениями первого порядка    (6.10)

Примером цепей первого порядка являются простейшие RL и RC цепи.

Переходные процессы в RL-цепях. Рассмотрим включение RL-цепи к источнику напряжения u(t) (рис. 6.1).

Из рис. 6.1 следует, что до коммутации ключ К разомкнут, поэтому ток i_L(0_–) = 0 и цепь находится при нулевых начальных условиях. В момент t = 0 ключом К замыкаем (осуществим коммутацию) цепь, подключив ее к источнику напряжения u(t). После замыкания ключа К в цепи начнется переходный процесс. Для его математического описания выберем в качестве независимой переменной i_L = i и составим относительно нее дифференциальное уравнение по ЗНК:    (6.11)

Уравнение (6.11) относится к линейным неоднородным дифференциальным уравнениям первого порядка типа (6.3), решение которого можно записать согласно (6.5) в форме    (6.12) где i_св — свободная составляющая тока, обусловленная свободными процессами, протекающими в цепи без участия источника u(t); i_np — принужденная составляющая тока, обусловленная действием источника напряжения u(t).

Свободная составляющая тока i_св есть общее решение однородного дифференциального уравнения    (6.13) и согласно (6.7)    (6.14) где А — постоянная интегрирования; р — корень характеристического уравнения типа (6.6);    (6.15)

Отсюда p = —R/L. Величина 1/|р| носит название постоянной времени цепи. В неразветвленной RL-цепи   = L/R.

Принужденная составляющая i_пp может быть определена как частное решение уравнения (6.11). Однако, как было указано выше, i_пp можно найти более просто методами расчета установившегося режима цепи. Рассмотрим два частных случая:

В первом случае принужденная составляющая может быть определена из установившегося режима:i_пp = U/R. Для нахождения постоянной интегрирования A перепишем (6.12) в форме i = Ае^–t /  + U/R и учтем начальные условия для i, а также первый закон коммутации (6.1):

Отсюда А = —U/R. Таким образом, закон изменения тока в RL-цепи определяется уравнением    (6.16)

Напряжение на индуктивности согласно (1.9)    (6.17)

Н а рис. 6.2 изображены графики зависимости i(t) и u_L(t). Анализ полученных уравнений (6.16) и (6.17) показывает, что чем больше постоянная времени цепи  , тем медленнее затухает переходной процесс. На практике принято считать переходной процесс законченным при t = (3...5) , при t = 3  ток достигает 95% своего установившегося значения, а при t = 5  — более 99%. Графически постоянная времени   может определиться как интервал времени на оси t от t = 0 до точки пересечения касательной к u_L (рис. 6.2), в указанный момент напряжение на u_L уменьшается в е раз по сравнению с начальным.

Анализ полученных результатов показывает, что при нулевых начальных условиях в момент t = 0₊индуктивность ведет себя как бесконечно большое сопротивление (разрыв цепи), а при t =   как бесконечно малое сопротивление (короткое замыкание цепи).

Для второго случая принужденная составляющая тока согласно §3.6  где  ,   = arctg( L/R). Постоянная интегрирования определяется из уравнения

Откуда  . Следовательно, закон изменения тока в цепи в этом случае будет    (6.18)

На рис. 6.3 изображена временная зависимость тока (6.18). Напряжение на индуктивности    (6.19) где U_mL =  LI_m.

Анализ уравнения (6.18) показывает, что в случае подключения цепи к источнику u(t) в момент, когда  _u =   ±  /2 в последней могут возникать сверхтоки. Если постоянная времени цепи   достаточно велика, то скачок тока в начальный период может достигать i_max   2I_m. Напротив, при включении цепи в момент, когда  _u =  , в ней сразу наступает установившийся режим. Аналогичная картина наблюдается и с напряжением на индуктивности (6.19).

В качестве второго примера расчета рассмотрим случай ненулевых начальных условий в RL-цепи (рис. 6.4). К моменту коммутации в данной цепи была запасена энергия магнитного поля, равная W_L = Li²(0_– )/2, где i(0_– ) = U/(R₀ + R). После коммутации в RL-цепи возникает переходный процесс, описываемый уравнением:    (6.20) т. е. i_пp = 0. Решая уравнение (6.20), находим с учетом (6.13) – (6.15):

Постоянную А находим из начального условия i(0_– ) и закона коммутации (6.1):

Окончательно закон изменения тока в переходном режиме описывается уравнением    (6.21)

Напряжение u_L определяется как    (6.22)

На рис. 6.5 изображены графики i и u_L. Следует отметить, что вся энергия W_L, запасенная в индуктивности с течением времени, расходуется на тепловые потери в R. При ненулевых начальных условиях L ведет себя как источник тока.

Переходные процессы в RС-цепях. При расчете переходных процессов в RС-цепях в качестве независимой переменной выбирают u_C. Затем также составляют дифференциальное уравнение для заданной RС-цепи, решение которого с учетом начальных условий для u_C(0) и определяет закон изменения напряжения на емкости.

Рассмотрим вначале RC-цепь при нулевых начальных условиях (рис. 6.6), которая подключается в момент t = 0 к источнику постоянного и(t) = U или синусоидального и(t) = U_msin( t +  _u ) напряжения. Переходный процесс в данной цепи описывается дифференциальным уравнением    (6.23) решение которого ищем также в форме суммы общего и частного решений, определяющих свободную и принужденную составляющие:    (6.24)

Свободная составляющая является решением однородного дифференциального уравнения    (6.25)    (6.26) где р определяется из характеристического уравнения

Величина RC носит название постоянной времени RC-цепи и обозначается через  .

Определим принужденную составляющую u_C пp для случая, когда u(t) = U = const. Из рис. 6.6 следует, что в установившемся режиме u_C пp = U. Следовательно, с учетом (6.24) и (6.26) уравнение для и_Cпримет вид и_C = Ae^–t /  + U. Для нахождения постоянной интегрирования А учтем нулевые начальные условия для u_C(0_–) и второй закон коммутации (6.2): u_C(0_–) = u_C(0₊) = 0 = A + U, откуда А = —U. Таким образом, получаем окончательно:    (6.27)

Ток в цепи определяется согласно (1.12):    (6.28)

На рис. 6.7 изображены графические зависимости u_С(t) и i(t).

Анализ полученных результатов показывает, что в момент t = 0₊ емкость С (при нулевых начальных условиях) ведет себя как короткозамкнутый участок. Напротив, при t =   емкость представляет собой бесконечно большое сопротивление (разрыв цепи для постоянного тока).

Рассмотрим случай гармонического воздействия. Нетрудно видеть что при этом    (6.29) где    (6.30) а напряжение

Постоянная А находится из начальных условий для u_C(0₊) при t = 0₊:

Окончательно закон изменения напряжения    (6.31)

На рис. 6.8 изображен график зависимости u_C(t). Анализ уравнения (6.31) показывает, что в случае неудачного включения при  _u =   –   и большой   в цепи могут возникать перенапряжения, достигающие на емкости величины u_Cmax   2U_mC. В случае удачного включения, когда  _u =  /2 –  , в цепи сразу наступает установившийся режим.

Ток в цепи    (6.32)

Рассмотрим теперь случай ненулевых начальных условий, когда емкость С, заряженная до напряжения U, разряжается на сопротивление R (рис. 6.9). К моменту коммутации в емкости была запасена энергия W_C = CU²/2. После коммутации возникает переходный процесс, определяемый уравнением    (6.33) т. е. имеет место свободный режим разряда (емкости):    (6.34)

Постоянную интегрирования А находим из начального условия для u_C(0₊) = U и закона коммутации (6.2):

Таким образом, получаем закон изменения напряжения на емкости    (6.35) и тока в цепи    (6.36)

Знак "–" в уравнении (6.36) для тока свидетельствует о том, что ток разряда направлен противоположно опорному направлению напряжения и_С в емкости (см. § 1.2). На рис. 6.10 приведены графики изменения напряжения и_С(t) и тока i(t) данной RС-цепи. Следует подчеркнуть, что вся запасенная энергия W_C емкости с течением времени преобразуется в элементе R в тепло. При ненулевых начальных условиях С ведет себя как источник напряжения.