
- •1.Электрическое поле, однородное и неоднородное. Работа по перемещению электрического заряда в однородном поле.
- •2.Напряжение и потенциал.
- •3.Явление электрического тока. Проводники первого и второго рода.
- •4.Электродвижущая сила. Вольт-амперные характеристики источников тока.
- •5.Работа и мощность электрического тока
- •6.Электрическая цепь постоянного тока. Закон Ома для участка цепи
- •7. Электрическая цепь с последовательным включением сопротивлений.
- •8. Разветвлённая электрическая цепь.
- •9. Законы Кирхгофа для разветвлённых цепей
- •10. Закон Джоуля - Ленца.
- •11. Метод контурных токов
- •12. Падение напряжения и потери в электрических цепях
- •13. Магнитное поле и магнитная цепь.
- •14. Основные характеристики магнитного поля
- •15. Ферромагнитные материалы в магнитном поле
- •16. Закон полного тока
- •17. Явление магнитного гистерезиса
- •18. Магнитная цепь. Магнитная проницаемость
- •19. Закон магнитной цепи. Закон полного тока в неоднородной магнитной цепи.
- •20. Расчет магнитных цепей
- •21. Закон электромагнитной индукции. Самоиндукция и взаимоиндукция
- •22. Потери от гистерезиса при перемагничивании. Вихревые токи. Вихревые токи
- •23. Переменный ток. Генерирование переменного тока
- •24. Мгновенное, действующее и среднее значение синусоидальных величин переменного тока
- •25. Электрические цепи однофазного синусоидального тока
- •26. Метод векторных диаграмм. Изобжениеэ.Д.С., напряжений и токов с помощью вращающихся векторов
- •27. Сложение и вычитание синусоидальных функций
- •28. Мгновенная мощность
- •29. Ёмкостной элемент в цепи переменного тока.
- •30. Индуктивный элемент в цепи переменного тока
- •31. Трёхфазный ток. Трёхфазные системы напряжений и токов
- •32. Мощность в цепи переменного тока (активная, реактивная, полная)
- •33. Цепь трёхфазного тока по схеме «Треугольник»
- •34. Цепь трёхфазного тока по схеме «Звезда». Фазные и линейные значения напряжений и токов
- •35. Рабочая точка. Выбор рабочей точки при расчете усилителя.
- •36. Усилитель оэ. Схема усилителя. Назначение элементов.
- •37. Вращающееся магнитное поле. Электрические машины (электродвигатели, электрогенераторы )
- •38. Электрические измерения. Системы электроизмерительных приборов
- •39. Принцип измерения тока, напряжения и мощности в цепях постоянного и переменного токов.
- •40. Электрические машины. Преобразование энергии в электрических машинах
- •41. Переходные процессы в цепях с индуктивностью
- •42. Переходные процессы в цепях, содержащих ёмкость
- •43. Полупроводниковые материалы. Ковалентная связь между атомами. Возбужденная проводимость. Понятие о дырке
- •44. Примесные полупроводники. Проводимость и концентрация носителей заряда; их зависимость от температуры
- •46. Выпрямительные свойства р-n перехода.
- •47. Ток Io и его зависимость от материала и температуры
- •48. Барьерная емкость диода
- •49. Генерация и рекомбинация носителей заряда. Неравновесное Состояние. Время жизни
- •50. Диффузионный биполярный транзистор. Основной параметр
- •51. Подвижность носителей заряда и её зависимость от температуры
- •54. Частотные свойства транзистора Error 404 (страница не найдена)
- •55. Трансформаторы. Принцип действия. Назначение
- •56. Мощность в цепи трехфазного тока
- •61. Вторичные источники питания. Стабилизаторы напряжения и тока
- •62. Логические элементы на биполярных транзисторах.Схемы не, или, и
- •63. Транзисторный ключ.Принцип работы, быстродействие
- •64. Бистабильные ячейки.Транзисторный триггер, принцип действия
- •65. Транзисторный триггер. Режим раздельного и общего входов
26. Метод векторных диаграмм. Изобжениеэ.Д.С., напряжений и токов с помощью вращающихся векторов
27. Сложение и вычитание синусоидальных функций
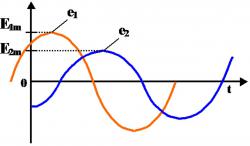
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями и представить в виде вращающихся векторов на декартовой или комплексной плоскости.
|
Запишем синусоидальные напряжения с помощью тригонометрических функций:
e1=E1msin(ω⋅t+φe1),
e2=E2msin(ω⋅t+φe2),
φe1>φe2(φe2>0)
Значения в скобках синуса называют фазами синусоид, а значения фазы в начальный момент времени - начальной фазой.
Величина ω называется циклической частотой:
ω=2⋅πT=2⋅π⋅f,[рад/с]
где
Т - период [c];
f - частота [Гц].
При совместном рассмотрении двух синусоидально изменяющихся величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз:
α=ω⋅t+φe1−(ω⋅t+φe2)=φe1−φe2
Если α=0, то говорят, что сигналы синфазны, если α=π, то говорят, что сигналы в противофазе. Если α=+π/2 - в квадратуре. Т.е. e2 отстаёт от e1 на угол α.
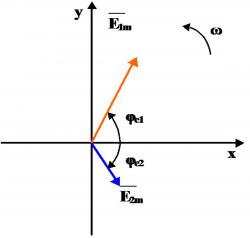
При изображении синусоидальных ЭДС, напряжений и токов вращающимися векторами на декартовой плоскости из начала координат проводят векторы, равные амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки с угловой скоростью ω. Фазовый угол отсчитывают от положительной оси абсцисс.
|
Проекции вращающихся векторов на ось ординат равны мгновенным значениям.
(отсюда начинается ответ на вопрос, до этого пояснение, что откуда берется)
Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, называют векторными диаграммами. При построении векторных диаграмм часто удобно принимать t=0. При этом сложение и вычитание синусоидально изменяющихся величин можно заменить сложением и вычитанием их векторов:
e3=e1+e2=E3msin(ω⋅t+φe3),
Eˉ3m=Eˉ1m+Eˉ2m
Результирующие напряжение также будет синусоидальным.
|
Определение амплитуды E3m и начальной фазы φe3 можно осуществить сложением изображающих их векторов.
Вычитание мгновенных значений можно заменить вычитанием изображающих векторов
Eˉ3m=Eˉ1m−Eˉ2m
|
28. Мгновенная мощность
(то что подчеркнуто рассказывать ему не надо, если он про это не спросит сам. Подчеркнутое поможет ответить на его возможные вопросы).
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:
|
|
Для единичного заряда на участке A-B:
|
|
Для всех зарядов:
|
|
Поскольку
ток есть не что иное, как количество
зарядов в единицу времени, то есть ![]() по
определению, в результате получаем:
по
определению, в результате получаем:
|
|
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:
|
|
Если участок цепи содержит резистор с электрическим сопротивлением R, то
|

 Р
Р
 Р
исунок
2 - Изображение синусоидальных
напряжений вращающимися векторами
Р
исунок
2 - Изображение синусоидальных
напряжений вращающимися векторами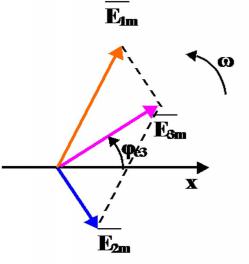 Р
исунок
3 - Изображение суммы двух синусоидальных
напряжений в виде вращающегося вектора
Р
исунок
3 - Изображение суммы двух синусоидальных
напряжений в виде вращающегося вектора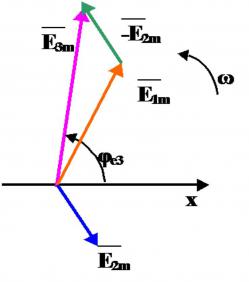 Р
исунок
4 - Изображение разности двух
синусоидальных напряжений в виде
вращающегося вектора
Р
исунок
4 - Изображение разности двух
синусоидальных напряжений в виде
вращающегося вектора