13 Поворот осей

ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

Рис. 3

П осмотрим, как изменяют­ся моменты инерции при по­вороте осей координат. Поло­жим, даны моменты инерции некоторого сечения относительно осей х, у (не обязательно центральных). Требуется определить J_u, J_v, J_uv  — моменты инерции относительно осей и, v, повернутых относительно первой системы на угол a (рис. 3).

Проектируем замкнутый четырехугольник ОАВСО на оси и и v. Так как проекция ломаной линии равна проекции замыкающей, на­ходим:

u = y sin a +x cos a,     v = y cos a — x sin a

 

В выражениях (3), подставив вместо x₁ и y₁ соответственно u и v, исключаем u и v

откуда

                                                                                                                     (5)

Рассмотрим два первых уравнения. Складывая их почленно, получим, что сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла a и при пово­роте осей остается постоянной. При этом

x² + y² = r²

где r — расстояние от начала координат до элементарной площадки (рис. 3). Таким образом,

                                              J_x + J_y = J_p

где J_p— полярный момент инерции

величина которого, естественно, не зависит от поворота осей ху.

С изменением угла поворота осей a каждая из величин J_u и J_v меняется, а сумма их остается неизменной. Следовательно, сущест­вует такое a, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент инер­ции принимает минимальное значение.

Дифференцируя выражение J_u (5) по a и приравнивая произ­водную нулю, находим

                                                                                                          (6)

При этом значении угла a один из осевых моментов будет наиболь­шим, а другой — наименьшим. Одновременно центробежный момент инерции J_uv при указанном угле a  обращается в нуль, что легко устанавливается из третьей формулы (5).

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, назы­ваются главными осями. Если они к тому же являются централь­ными, то тогда они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Для определения этого первые две формулы (5) перепишем в виде

Далее исключаем при помощи выражения (6) угол a. Тогда

Верхний знак соответствует максимальному моменту инерции, а нижний — минимальному. После того как сечение вычерчено в масштабе и на чертеже показано положение главных осей, нетрудно установить, которой из двух осейсоответствует максимальный и которой — минимальный мо­мент инерции.

Если сечение имеет ось симметрии, то эта ось всегда будет главной .Центробежный момент инерции части сечения, расположенной по одну сторону от оси, будет равен моменту части, расположенной по другую сторону, но противоположен ему по знаку. Сле­довательно, J_ху= 0 и оси х и у являются глав­ными.

14 Удлинение стержня и закон Гука Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим - свободным, к которому приложена центральная продольная сила Р (рис. 2.2). До нагружения стержня его длина равнялась l -после нагружения она стала равной l + Dl (рис. 2.2). Величину Dl называют абсолютным удлинением стержня.

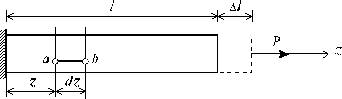Рис. 2.2 Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация e остается одной и той же по длине стержня и равной (2.1)

Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.2). При растяжении он увеличит свою длину на величину D dz и его деформация составит: 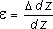(2.2) В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде:s = E e . (2.3) Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода. Из совместного рассмотрения уравнений (2.2) и (2.3) получим: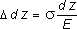 ,откуда с учетом того, что и ,окончательно получим: Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение F = const и нагружен по концам силой Р, то из (2.4) получим (2.5) При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций: , где a - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:. 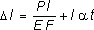(2.7)

Коэффициент Пуассона характеризует упругие свойства материала. При приложении к телу растягивающего усилия оно начинает удлиняться (то есть длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5. (Измеряется в относительных единицах (мм/мм, м/м))

где ν — коэффициент Пуассона.

• — деформация в поперечном направлении (отрицательный для осевого растяжения, положительный для осевого сжатия)

• — продольная деформация (положительный для осевого растяжения, отрицательный для осевого сжатия).