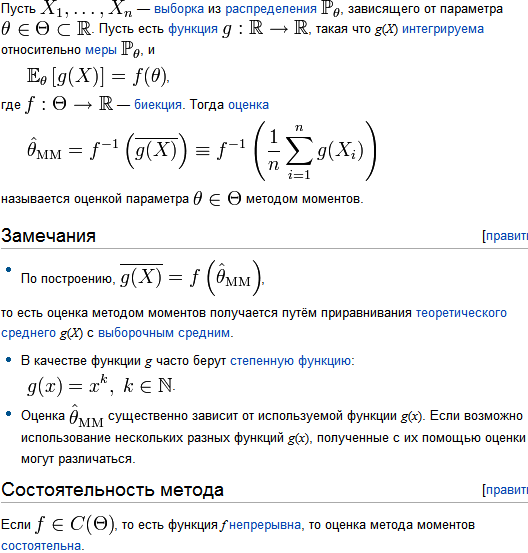
14. Метод моментов

Метод моментов - теоретические моменты СВ  оцениваются выборочными моментами СВ .

Алгоритм оценки неизвестного параметра методом моментов:

1.Вычисляются k первых теоретических моментов по формулам:

Начальные теоретические моменты:

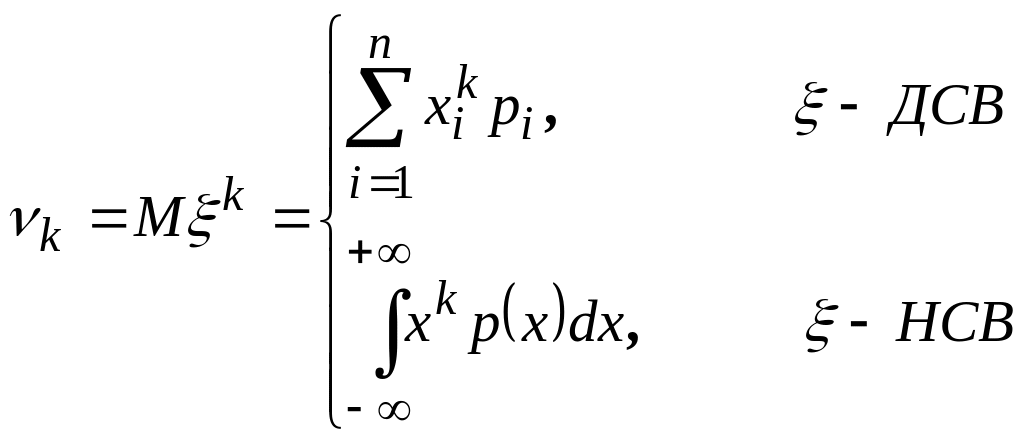k = 1,2,…,n

Центральные теоретические моменты:

Число неизвестных параметров равно k.

При

При

2.Находят по выборке x₁, x₂, …, x_n значения СВ 

Выборочные моменты 1, 2, …, k – того порядка:

Выборочный начальный момент k – того порядка:

Выборочный центральный момент k – того порядка:

3.Приравнивают теоретические и выборочные моменты. В результате получают систему из k уравнений с k неизвестными, решая которую находят оцениваемые параметры

15. Метод максимального правдоподобия.

Рассмотрим случайную выборку x₁, x₂, …, x_n из генеральной совокупности значений СВ . Будем предполагать, что плотность вероятности зависит от параметра , т. е. Имеет вид .

Функция правдоподобия непрерывной СВ  с плотностью вероятности :

Функция правдоподобия дискретной СВ , для которой распределение вероятности зависит от параметра :

Для конкретной выборки x₁, x₂, …, x_n функция является функцией одного неизвестного параметра (может быть несколько параметров).

Этот метод состоит в том, что в качестве оценки параметра принимается , для которого функция правдоподобия принимает свое максимальное значение по данной выборке, т. е. .

Задача сводится к нахождению максимума функции правдоподобия.

Т. к. функция и функция имеют экстремумы в одних и тех же точках, то для простоты вычислений вместо будем рассматривать - логарифмическая функция правдоподобия.

Алгоритм нахождения точечной оценки с помощью метода максимального правдоподобия:

1. Составляем функцию правдоподобия и логарифмическую функцию правдоподобия по данной выборке.

2. Решаем уравнение правдоподобия:

или .

Если оцениваемых параметров несколько , то для их нахождения нужно решить систему m уравнений:

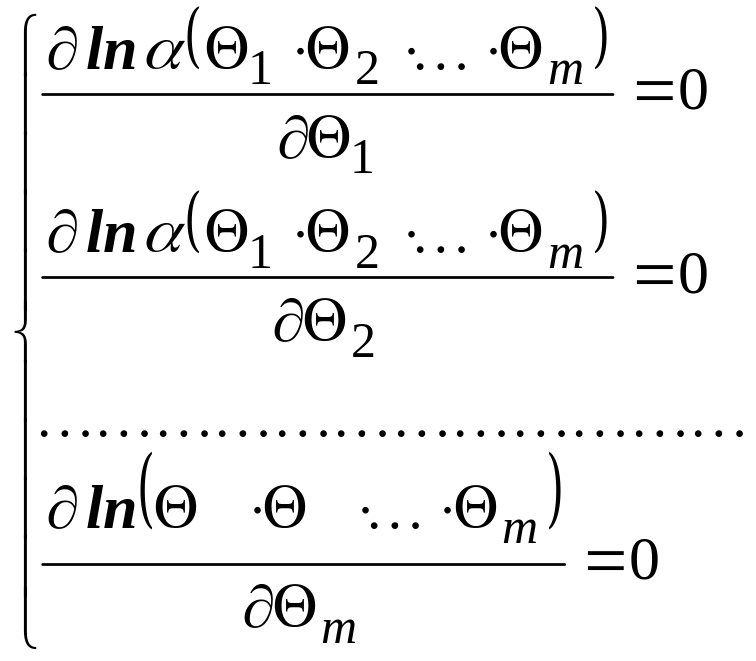
Найденное значение из решения уравнения или системы и является искомой оценкой.

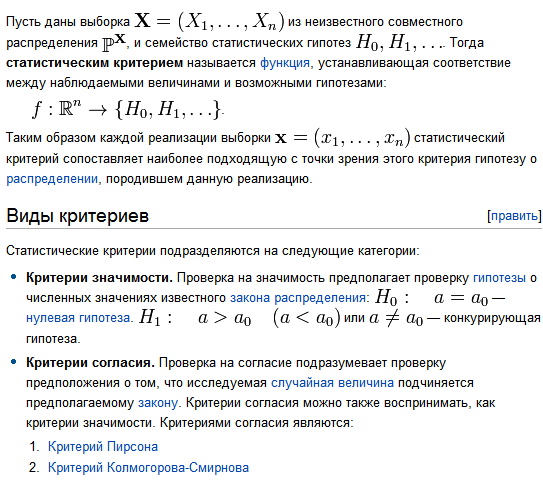
18. Элементы проверки статистических гипотез.

Опр. Статистической гипотезой наз-ся любое предположение о виде или параметре неизвестного закона распред-я. Обычно проверяемую гипотезу обозначают через Но.;

Пусть дан вариационный ряд.

возмож-ые знач. признака Х	Х1	Х2	…	Хк	
число объектов	n1	n2	…	nk	n

Гипотеза Но: {Обязательно формулировать при задачах} Случайная величина Х-з/п рабочего имеет нормальный закон распред-я с параметрами а=151,6; =24,3 (отклонение эксперем-х данных от теорет-х вызвано случ-ми факторами). Экспериментальные данные ni- эмпирические частоты (см. вар. ряд). (i=1,2,…m, где m- число

тнтервалов). Теоретич-ие данные (см. гипотезу Но);

; .

В качестве меры расхождения между эксперим-ми и теорит-ми данными испол-ют статистику (хи). Статистика – случайная вел. с парам.; При

достаточно большом n закон распределения статистики известен и не зависит от

закона распред-я случ. величины Х. При n эта статистика имеет так называемое распределение с K=m-S-1 степенями свободы. (m-число интервалов; S- число параметров закона распр-я Х).; Опр.: Уравнением значимости наз-ся вер-ть отвергнуть гипотезу Но, когда она верна. - ур-нь значимости (тоже что и эпсило). Опр.:

Пороговым значением - наз-ся число, определ-ое равенством . Опр.: Правило по которому гипотеза Но приним-ся или отвергается наз-ся статистическим критерием.

11-12. выборочная дисперсия S² повторной и бесповторной выборок есть смещенная и состоятельная оценка генеральной дисперсии σ². выборочная а) выборка повторная: найдем мат. ожидание

б) выборка бесповторная так же как и повторная, т.е. S² – смещенная оценка σ². так как (n-1)/n<1 и М(S²)< σ², то выборочная дисперсия занижает генеральную дисперсию. Поэтому, заменяя σ² на S², мы допускаем систематическую погрешность в меньшую сторону. Чтобы ее ликвидировать, достаточно ввести поправку, умножив S² на n/(n-1). Тогда получим «исправленную» выборочную дисперсию ^ Очевидно, что т.е. ^ S² явл. Несмещенной и состоятельной оценкой генеральной дисперсии σ².

13. Понятие эффективности оценок.

15. метод максимального правдоподобия.

14. Метод моментов.

17. Довер. интервалы для мат. ожидания

16.Доверит. интервал …

19. Статистический критерий.

25. Линейная регрессия.