
- •6. Распределение «xи квадрат».
- •7. Распределение Стьюдента.
- •8. Распределение Фишера.
- •17« Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях »
- •22. Гипотезы сравнения о равенстве мх при известной дисперсии.
- •23. Гипотезы сравнения о равенстве dx.
- •1. Задачи математической статистики. Генеральная совокупность. Выборка.
- •2. Генеральная совокупность. Выборка.
- •14. Метод моментов
- •15. Метод максимального правдоподобия.
- •Алгоритм нахождения точечной оценки с помощью метода максимального правдоподобия:
- •18. Элементы проверки статистических гипотез.
6. Распределение «xи квадрат».
Пусть Xi,
![]() —нормальные
независимые случайные величины, причем
математическое ожидании каждой из них
равно нулю, а среднее квадратическое
отклонение (или дисперсия)—единице.
Тогда сумма квадратов этих величин
—нормальные
независимые случайные величины, причем
математическое ожидании каждой из них
равно нулю, а среднее квадратическое
отклонение (или дисперсия)—единице.
Тогда сумма квадратов этих величин
![]() распределена по закону Х2 с k=n
степенями свободы. Если же эти величины
Хi связаны одним
линейным соотношением, например
распределена по закону Х2 с k=n
степенями свободы. Если же эти величины
Хi связаны одним
линейным соотношением, например
![]() ,
то число степеней свободы k=n-1.
,
то число степеней свободы k=n-1.
Плотность этого
распределения![]() ,
где
,
где
![]() —гамма-функция;
в частности, Г(n+1)=n!
—гамма-функция;
в частности, Г(n+1)=n!
Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
7. Распределение Стьюдента.
Пусть Z—нормально
распределенная величина, причем M(Z)=0,
G2=1, т.е. Z~N(0,1),
а V—независимая от Z
величина, которая распределена по закону
Х2 с k степенями
свободы. Тогда величина![]() имеет распределение, которое называют
t—распределением или
распределением Стьюдента (псевдоним
английского статистика В.Госсета), с k
степенями свободы. С возрастанием числа
степеней свободы распределение Стьюдента
быстро приближается к нормальному.
имеет распределение, которое называют
t—распределением или
распределением Стьюдента (псевдоним
английского статистика В.Госсета), с k
степенями свободы. С возрастанием числа
степеней свободы распределение Стьюдента
быстро приближается к нормальному.
Плотность
распределения случайной величины t
имеет вид
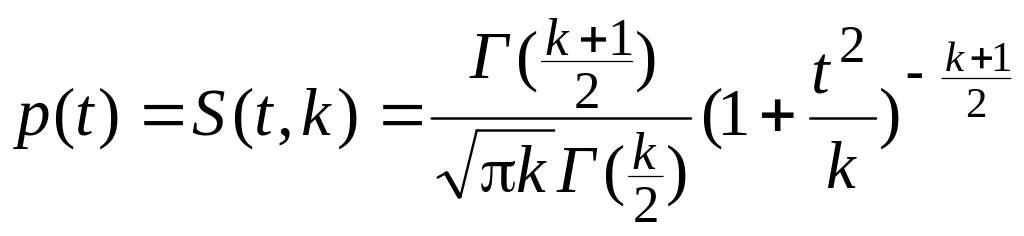 ,
,
![]() .
.
Случайная величина
t имеет математическое
ожидание Mt=0,
![]() (k>2).
(k>2).
8. Распределение Фишера.
Если U
и V—независимые случайные
величины, распределенные по закону Х2
со степенями свободы k1
и k2, то величина
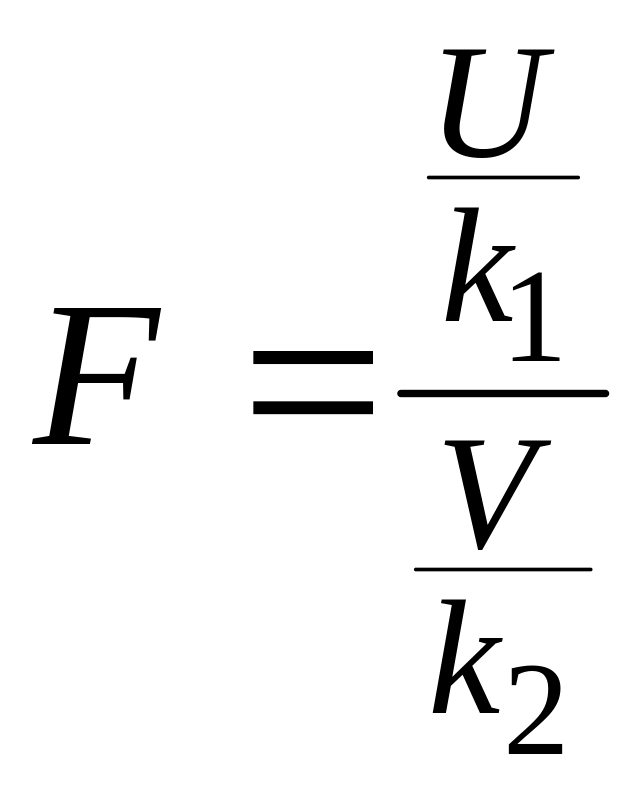 имеет распределение Фишера F
со степенями свободы k1
и k2. Плотность этого
распределения
имеет распределение Фишера F
со степенями свободы k1
и k2. Плотность этого
распределения
![]() ,
где
,
где
 .
.
Распределение Фишера F определяется двумя параметрами—числами степеней свободы.
17« Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях »
Пусть производится n независимых испытаний по схеме Бернулли, в каждом из которых вероятность появления события А постоянна и равна р, 0 < р <1.
Определим вероятность
того, что при n испытаниях
относительная частота появления события
А отличается от постоянной вероятности
р не более чем на
![]() ,
где
>0,
произвольное бесконечно малое.
,
где
>0,
произвольное бесконечно малое.
![]()
Рассмотрим выражение
![]() ;
;

Итак,
![]()
![]()
По интегральной теореме Лапласа:
![]()
![]()
![]()
![]() (1)
(1)
С использованием формулы (1) решаются задачи трёх типов:
1) прямое применение формулы.
2) по данным условия задачи найти n – число испытаний.
3) по данным условия задачи найти .
Формула (1) имеет большое практическое применение. Покажем это на различных задачах, приведенных в параграфе.
22. Гипотезы сравнения о равенстве мх при известной дисперсии.
Предположим,
что
![]() известны. H0: a1=a2.
В качестве оценок возьмем
известны. H0: a1=a2.
В качестве оценок возьмем
 .
Критическая область
.
Критическая область
![]() .
.
![]() ,
т.к.
,
т.к.
![]() -несмещенная
оценка a1
-несмещенная
оценка a1
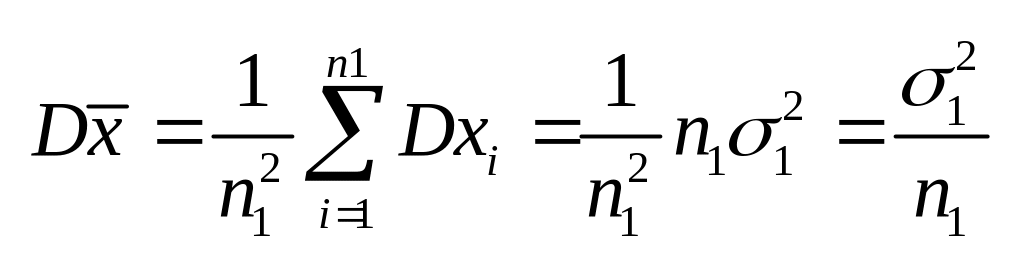 .
Т.о
.
Т.о
 ,
аналогично
,
аналогично
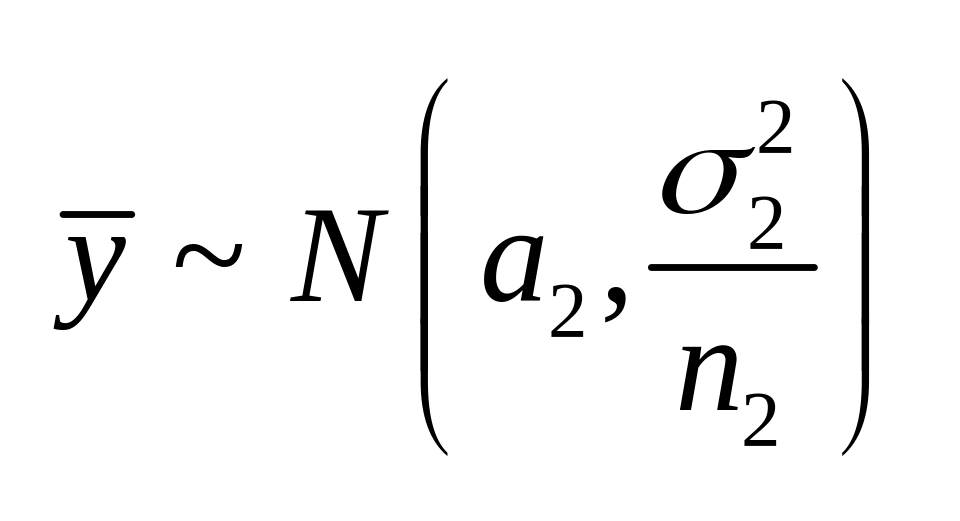
![]() .
.![]() .
.
 Таким
образом:
Таким
образом:
 В качестве статистики критерия берем
случайную величину
В качестве статистики критерия берем
случайную величину

