28. Частичные булевы функции, их минимизация по матрицам в коде Грэя. Метод Закревского

Определение. Неполностью определенной (частичной) бу­левой функцией f_х(x₁,... ,x_n) назовем однозначное отображение подмножества M булева пространства B_n в булево множество B, т.е. .

Как видно из определения, частным случаем неполностью опре­деленной булевой функции является булева функция: ее областью определения является все булево пространство. Булеву функцию также называют полностью определенной булевой функцией.

Неполностью определенная булева функция может быть зада­на различными способами, аналогичными способам задания буле­вой функции, в частности, таблицей истинности, матрицей Грея и характеристическими множествами.

Для нахождения всех максимальных интервалов неполностью определенной функции f_х(x₁,..., x_n) можно применить алгоритм Квайна-Мак-Класки или алгоритм Блейка-Порецкого к ее доопре­делению f(x₁,...,x_n), которое удовлетворяет условию: , а затем исключить из найденных интервалов те, которые не содержат ни одной точки функции f_х(x₁,..., x_n). Таблица Квайна неполностью определенной функции f_x(x1,... ,x_п) строится ана­логично таблице Квайна булевой функции.

Алгоритм поиска кратчайшей ДНФ неполностью опре­деленной булевой функции (основан на нахождении всех мак­симальных интервалов функции, построении таблицы Квайна и поиске кратчайшего покрытия этой таблицы).

Начало. Задана частичная булева функция f_х(x₁,..., x_n).

Шаг 1. Находим любым алгоритмом все максимальные интер­валы функции f_х(x₁,..., x_n).

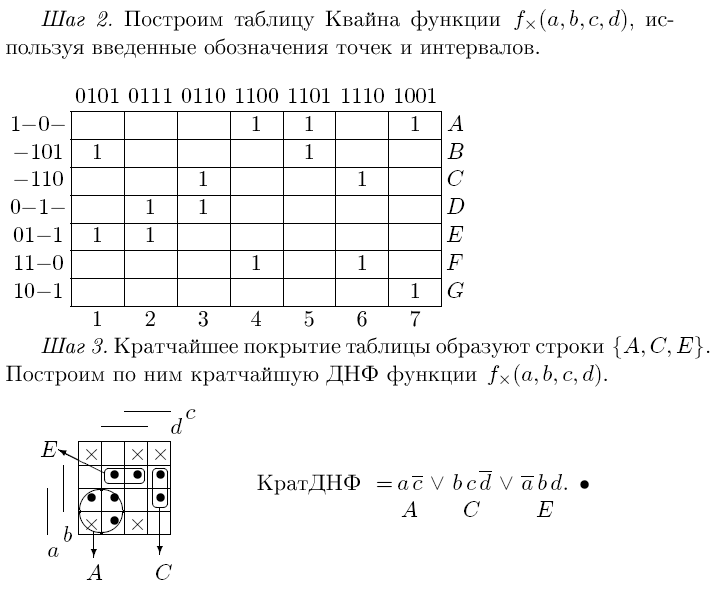
Шаг 2. Строим таблицу Квайна функции f_x(x₁, . . . ,x_n).

Шаг 3. Находим кратчайшее покрытие таблицы Квайна, а по покрытию - кратчайшую ДНФ функции f_х(x₁,..., x_n).

Конец.

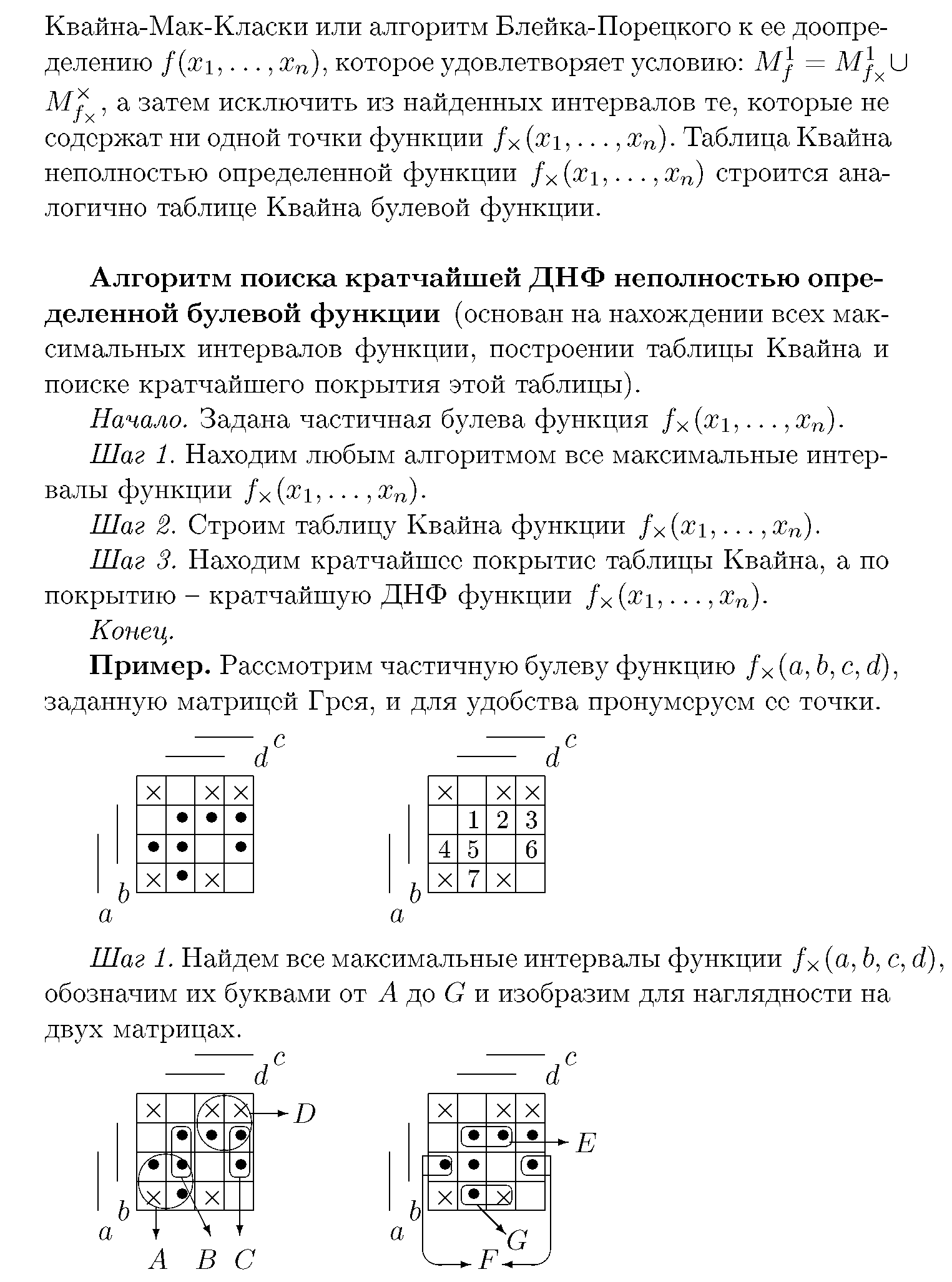
Алгоритм Закревского (ориентирован на матричное пред­ставление функции и визуальный способ решения).

Начало. Задана матрица Грея неполностью определенной бу­левой функции f_х(x₁,...,x_n).

Шаг 1. Для каждой точки вычислим цену - количество со­седних ей векторов из множества . Все точки будем считать неотмеченными.

Шаг 2. Среди неотмеченных точек рассмотрим точку мини­мальной цены и найдем все максимальные интервалы, которым она принадлежит. Выберем из них тот максимальный интервал, который содержит наибольшее число неотмеченных точек. Если таких интервалов несколько, то выберем из них интервал макси­мальной мощности.

Шаг 3. Включим выбранный интервал в решение и отметим его точки. Если не все точки отмечены, то идем на шаг 2.

Конец. Включенные в решение интервалы задают приближен­ную кратчайшую ДНФ функции

29. Метод конкурирующих интервалов для минимизации частичной булевой функции.

Метод конкурирующих интервалов. Этот ме­тод поиска приближенной кратчайшей ДНФ неполностью опре­деленной булевой функции не ориентирован на ее пред­ставление матрицей в коде Грея, а значит, может применяться к булевой функции большого числа переменных.

Перед изложением метода введем необходимые определения.

Рассмотрим частичную булеву функцию f_х(x₁,..., x_n), ее точ­ку α и допустимый интервал I.

Определение. Минимальным расширением интервала I до точки α (обозначается [I,α]) называется интервал I' минималь­ной мощности, удовлетворяющий условиям:

Как следует из определения, интервал [I, α] строится так:

• внутренние компоненты интервала I остаются внутренними и в интервале [I, α],

• внешние компоненты интервала I сохраняют свое значение в интервале [I, α], если они совпадают с соответствующими ком­понентами α,

• внешние компоненты интервала I становятся внутренними в интервале [I, α], если они ортогональны соответствующим компо­нентам α.

Пример.

Определение. Интервал I и точка α называются совмести­мыми, если интервал [I,α] является допустимым для функции f_х (x_i, . . . , x_n).

Перейдем теперь к изложению метода конкурирующих интер­валов. Метод является итерационным. На каждой итерации ме­тода имеется некоторое частичное решение поставленной задачи, которое улучшается по определенным правилам. В данном случае частичным решением является множество допустимых интерва­лов функции. На каждой итерации будем изменять решение, либо добавляя в него новый интервал, либо расширяя один из имею­щихся интервалов. При этом желательно как можно меньше изме­нять частичное решение, то есть добавлять интервал наименьшей мощности или расширять интервал по наименьшему числу ком­понент.

Пусть на k-й итерации имеются частичное решение U_k и мно­жество M_k точек функции, не содержащихся ни в одном интерва­ле из U_k (на первой итерации ). Построим бу­леву матрицу совместимости R_k, строкам которой сопоставим точки из M_k, а столбцам - интервалы из U_k. Элемент, стоящий на пересечении i-й строки и j-ro столбца, равен единице, если i-я точка совместима с j-м интервалом. Далее будем обозначать стро­ки и столбцы матрицы совместимости символами сопоставленных им точек и интервалов.

Пусть строка α матрицы совместимости не содержит единиц. Это означает, что в множестве U_k нет ни одного интервала, сов­местимого с точкой α, то есть ни один интервал не может быть расширен на множестве так, чтобы расширение вклю­чало точку α. Значит, в множество U_k следует добавить интервал, совместимый с α. Такой интервал наименьшей мощности это сама точка. Отсюда вытекает следующее правило.

Правило строки без единиц. Если в матрице совместимости есть строка, не содержащая ни одной единицы, то она удаляется из матрицы. В матрицу добавляется столбец, которому сопоста­вляется вектор из удаленной строки.

Правило столбца без единиц. Если в матрице совместимости есть столбец, не содержащий ни одной единицы, то он удаляет­ся из матрицы. Интервал из удаленного столбца расширяется до максимального и добавляется в окончательное решение.

Правило столбца с одной единицей. Если в матрице совмести­мости есть столбец I, содержащий ровно одну единицу (в строке α), то эта строка удаляется из матрицы, а интервал I заменяется на интервал [I, α].

Определение. Рангом столбца матрицы совместимости на­зовем ранг сопоставленного столбцу интервала.

Правило столбца наибольшего ранга. Если к матрице совме­стимости не применимо ни одно из трех предыдущих правил, то в ней выбирается столбец I наибольшего ранга. Среди совместимых с ним точек находится точка α с минимальным числом компонент, ортогональных внешним компонентам интервала I. Из матрицы удалются строки, которым сопоставлены точки из [I, α]. Интер­вал I заменяется на [I, α] и столбец I пересчитывается.