26. Частичные булевы функции, способы их задания, доопределение

Определение. Неполностью определенной (частичной) бу­левой функцией f_х(x₁,... ,x_n) назовем однозначное отображение подмножества M булева пространства B_n в булево множество B, т.е. .

Как видно из определения, частным случаем неполностью опре­деленной булевой функции является булева функция: ее областью определения является все булево пространство. Булеву функцию также называют полностью определенной булевой функцией.

Неполностью определенная булева функция может быть зада­на различными способами, аналогичными способам задания буле­вой функции, в частности, таблицей истинности, матрицей Грея и характеристическими множествами.

1. Задание неполностью определенной булевой функ­ции таблицей истинности. В левой части таблицы истинности представляются, как и раньше, все векторы булева пространства, а в ее правой части либо перечисляются значения функции, либо указывается специальный символ х (если набор в область опре­деления не входит).

2. Задание неполностью определенной булевой функ­ции характеристическими множествами. К двум известным нам характеристическим множествам 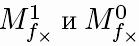добавляатся тре­тье, , состоящее из наборов, на которых функция не определе­на (для задания функции достаточно указать любые два из трех множеств).

3. Задание неполностью определенной булевой функ­ции матрицей Грея. В матрице Грея тем же символом х отме­чаются клетки, не входящие в область определения.

Неполностью определенная булева функция не может быть за­дана формулой, так как значение формулы может быть вычисле­но на всех наборах из Bⁿ.

Определение. Доопределением неполностью определенной бу­левой функции f_х(x₁,...,x_n) назовем любую булеву функцию f(x₁,..., x_n), удовлетворяющую условиям:

Это означает, что значения любого доопределения должны совпадать со значениями неполностью определенной булевой функ­ции f_х(x₁,... ,x_n) на наборах из характеристических множеств , и, в то же время, доопределение может принимать любые значения на наборах из множества . Из этого и из те­оремы о числе векторов с очевидностью следует утверждение.

Утверждение о числе доопределений. Число различ­ных доопределений неполностью определенной булевой функции

Пример.

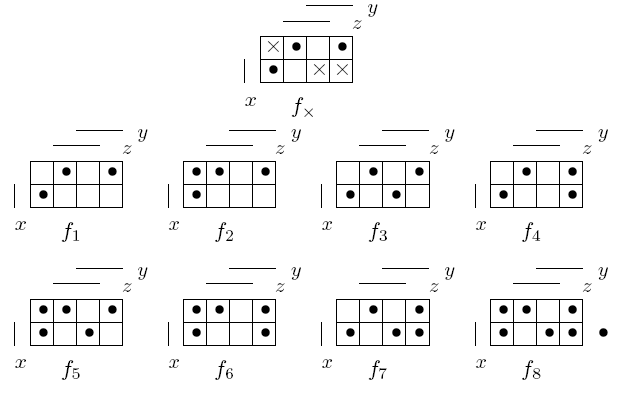
27.Частичные булевы функции, точный метод их минимизации

Определение. Неполностью определенной (частичной) бу­левой функцией f_х(x₁,...,x_n) назовем однозначное отображение подмножества M булева пространства B_n в булево множество B, т.е. .

Как видно из определения, частным случаем неполностью опре­деленной булевой функции является булева функция: ее областью определения является все булево пространство. Булеву функцию также называют полностью определенной булевой функцией.

Неполностью определенная булева функция может быть зада­на различными способами, аналогичными способам задания буле­вой функции, в частности, таблицей истинности, матрицей Грея и характеристическими множествами.

Определение. Минимизировать неполностью определенную булеву функцию - это значит выбрать среди кратчайших ДНФ всех ее доопределений самую короткую ДНФ.

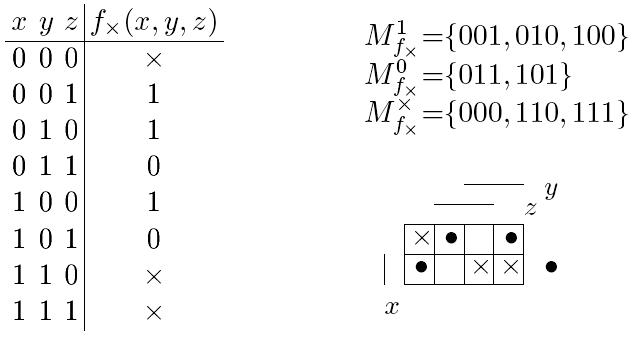
Пример. Для рассмотренной в предыдущем примере (26 билет) непол­ностью определенной булевой функции f_х(x, y, z) перебор крат­чайших ДНФ всех восьми доопределений приводит к следующе­му результату: самой короткой оказывается кратчайшая ДНФ до­определения f₆(x,y,z).

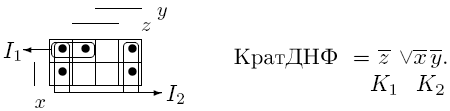
Таким образом, тот факт, что неполностью определенная буле­ва функция задается не на всем булевом пространстве, а лишь на его подмножестве, мы используем для такого "выгодного" доопре­деления функции, которое приводит к наиболее короткой ДНФ и к наиболее простой схеме, реали­зующей функцию.

Конечно, как и в случае булевых функций, возможны дру­гие постановки задачи минимизации неполностью определенных булевых функций - можно, например, искать ее приближенную кратчайшую ДНФ.

Определение. Интервал I назовем допустимым для непол­ностью определенной булевой функции f_х(x₁,..., x_n), если он удо­влетворяет условиям:

Определение. Интервал I назовем максимальным для непол­ностью определенной булевой функции, если он допустим для этой функции, и не существует другого допустимого для нес ин­тервала I' такого, что

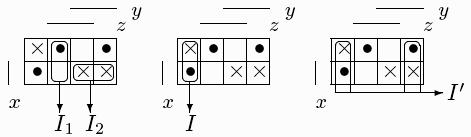
Пример. На левой матрице Грея изображены два недопустимых интервала на средней – допустимый интервал I = -00 (но не максимальный), на правой - максималь­ный I' =-­­-0.