Равносильность формул

Определение. Две формулы F' и F" называются равносиль­ными, если они задают равные функции. В этом случае пишут F' = F".

Доказывать равносильности можно с помощью таблиц истин­ности или рассуждений, опирающихся на свойства элементарных булевых функций.

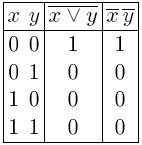
Пример. Докажем равносильность , построив та­блицы истинности для левой и правой формул.

Основные равносильности

К основным относят следующие равносильности, которые ре­комендуется запомнить и применять при упрощении формул.

11) Формула Шенона.Докозательство

Определение. Разложением Шеннона называется следую­щее разложение булевой функции f(x₁, ...,x_n) по переменной x_i:

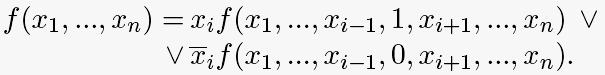
Доказательство (не умоляя общности, для i =1). Покажем, что формула верна в обоих случаях: для x₁ = 0 и x₁ = 1.

Если x₁ = 0, то f (0, x₂, ... , x_n) = 0 f (1, x₂, ... , x_n)  1  f (0, x₂, ... , x_n) =

= f (0, x₂, ... , x_n).

Если x₁ = 1, то f (1, x₂, ... , x_n)  = 1 f (1, x₂, ... , x_n)  0  f (1, x₂, ... , x_n) = = f (0, x₂, ... , x_n).

Оп ределение. Сомножитель f (x₁, ..., x_i -1, 1, x_i+1,... , x_n) в формуле Шеннона называется коэффициентом разложения функции f (x₁, x₂, ... , x_n) по переменной x_i при x_i, а сомножитель f (x₁, ..., x_i -1, 0, x_i+1,... , x_n) — коэффициентом разложения функции f (x₁, x₂, ... , x_n) по   x_i при .

Пример. Функцию разложим по переменной x:

12) Разложение функции по k переменным. Доказательство

Разложим функцию f(x₁, ...,x_n) последовательно по двум пе­ременным: сначала саму функцию по переменной x₁, затем коэф­фициенты разложения по переменной x₂.

Рассмотрим булеву функцию f (x₁, x₂, ... , x_n) и, используя формулу Шеннона, последовательно разложим функцию

- по первой переменной,

- по двум первым переменным,

- по k первым переменным.

1. Разложим функцию по первой переменной:

f (x₁, x₂, ... , x_n) = x₁  f (1, x₂, ... , x_n)  x₁ f ( 0, x₂, ... , x_n).

2. Разложим в полученной формуле оба коэффициента разложения по второй

переменной:

f (x₁, x₂, ... , x_n) = x₁  f (1, x₂, ... , x_n)  x₁ f ( 0, x₂, ... , x_n) =

= x₁  [ x₂ f (1,1, x₃, ... , x_n) x₂ f (1,0, x₃, ... , x_n) ] 

x₁ [ x₂ f (0,1, x₃, ... , x_n) x₂ f (0,0, x₃, ... , x_n) ] =

= x₁ x₂ f (1,1, x₃, ... , x_n)  x₁x₂ f (1,0, x₃, ... , x_n) 

x₁ x₂ f (0,1, x₃, ... , x_n) x₁x₂ f (0,0, x₃, ... , x_n) =

[ свернем последнюю формулу в более короткую, используя следующие

обозначения: x = x¹ и x = x⁰, то есть x^с, где c  {0,1}, и условимся

читать символы x^с как “x в степнени c “]

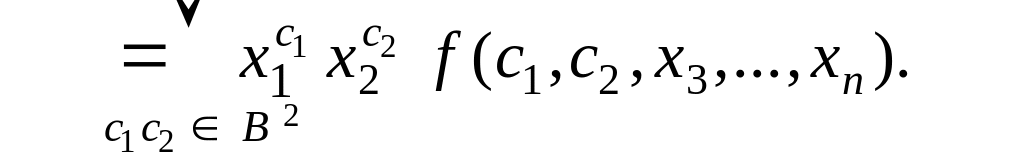
3. По аналогии с предыдущей формулой запишем формулу разложения

функции по k переменным: и докажем, что данное разложение верно.

Доказательство. Подставим в левую и правую части равенства произвольный набор a₁ a₂ ... a_n:

Упростим правую часть, рассуждая следующим образом. Нетрудно проверить, что 1, если и только если a_i = c_i (в самом деле: 0 ⁰ = 1, 1¹ = 1, но 0 ¹ = 0 и 1⁰ = 0), поэтому конъюнкция равна единице лишь в единственном случае, когда наборы a₁ a₂ ... a_k и с₁ с₂ ... с_k совпадают. А это значит, что она не обращает в ноль лишь одно слагаемое правой части — то, для которого a₁ a₂ ... a_k = с₁ с₂ ... с_k и в котором сама обращается в единицу. Подставив в ставшееся слагаемое a₁ a₂ ... a_k вместо с₁ с₂ ... с_k , получим

13) Получение СовДНФ из разложения функции по переменным. Утверждение о существовании и единственности СовДНФ.Алгоритм построения СовДНФ по таблице истинности функции.

Применив формулу разложения булевой функции f (x₁, x₂, ... , x_n) по k переменным при   k = n, получим:

Поскольку коэффициентами разложения f (c₁, c₂, ... , c_n) в этой формуле являются значения функции f (x₁, x₂, ... , x_n) на всевозможных наборах c₁ c₂ ... c_n, то возможны два случая:

- если набор c₁ c₂ ... c_n  M⁰ ( f ), то f (c₁, c₂, ... , c_n ) = 0 и поэтому обращается в 0 соответствующее слагаемое правой части;

- если набор c₁ c₂ ...c_n  M¹ ( f ), то f(c₁, c₂, ... , c_n ) = 1 и слагаемое упрощается.

В результате имеем формулу разложения функции по всем переменным:

Определение. Совершенная дизъюнктивная нормальная форма булевой функции , или СовДНФ, — это формула вида:

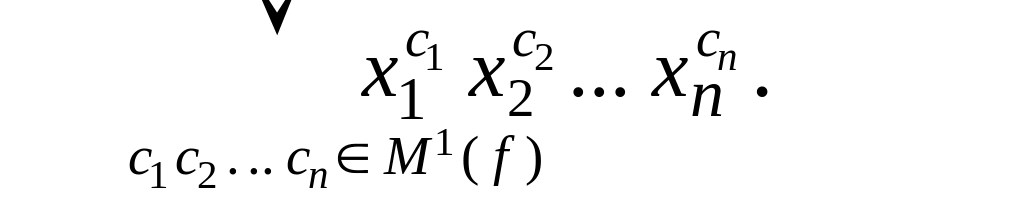
Утверждение о единственности СовДНФ

Любая булева функция, кроме константы 0, представима совершенной дизъюнктивной нормальной формой, единственной для данной функции.

Алгоритм построения СовДНФ (по таблице истинности) вытекает из определения СовДНФ и состоит в циклическом выполнении следующих шагов:

Шаг 1: в векторе – столбце значений функции выбирается очередная единица. Если единицы исчерпаны, то идем на конец.

Шаг 2: по набору значений аргументов выбранной строки формируется конъюнкция всех аргументов с соблюдением следующего правила: если i – я компонента набора 0, то i – я переменная входит в конъюнкцию в степени 0 (с инверсией), иначе – в степени 1 (без инверсии). Полученная конъюнкция добавляется в формулу как очередное слагаемое. Идем на шаг 1.

Конец.

Пример.

Соединив полученные конъюнкции знаками дизъюнкции, получим:

14) Получение СовКНФ из разложения функции по переменным. Утверждение о существовании и единственности СовКНФ. Алгоритм построения СовКНФ по таблицк истинности.

Пусть дана функция f(x₁, x₂, ... , x_n). Представим ее инверсию СовДНФ:

Инвертируем обе части этого равенства:

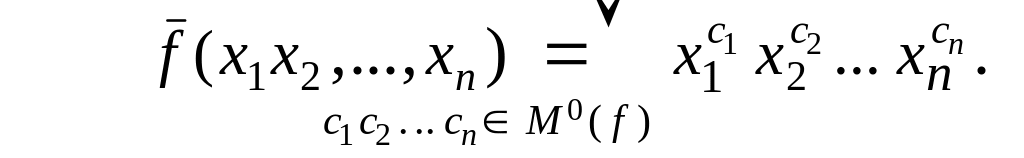
По законам двойного отрицания и де Моргана имеем:

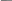
[ заметив, что , так как при c = 0 x = x, а при c = 1x  =x , получим ]

Определение. Совершенная дизъюнктивная нормальная форма функции

f(x₁, x₂, ... , x_n), или СовКНФ, — это формула вида:

Сформулируем утверждение с очевидностью вытекающее из СовКНФ.

Утверждение о единственности СовКНФ

Любая булева функция, кроме константы 1, представима cовершенной конъюнктивной нормальной формой, и она единственна для данной функции.

Алгоритм построения СовКНФ по таблице истинности вытекает из определения СовКНФ и состоит в циклическом выполнении следующих шагов:

Шаг 1: в векторе - столбце значений функции выбирается ноль. Если нули исчерпаны, то идем не конец.

Шаг 2: по набору значений аргументов выбранной строки формируется дизъюнкция всех аргументов с соблюдением следующего правила: если i-я компонента набора равна 0, то i-я переменная входит в дизъюнкцию в степени 1 (без инверсии), иначе – в степени 0 (с инверсией). Полученная дизъюнкция добавляется в формулу как очередной сомножитель. Идем на шаг 1.

Конец.

Пример.

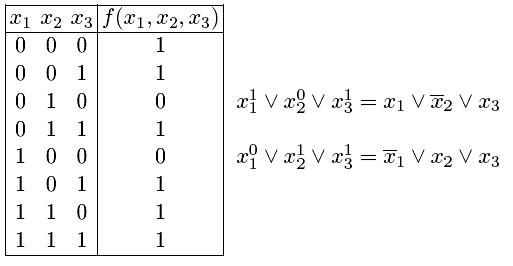
Соединив полученные дизъюнкции знаками конъюнкции, имеем:

15) Двойственная функция и двойственная формула.Принцип двойственности.

Определение. Булева функция f*(x1, ...,x_n) называется двой­ственной булевой функции f(x1,..., х_п), если она получена из функ­ции f(x1, ...,х_п) инверсией всех аргументов и самой функции, т.е.

Определение. Формула F* называется двойственной форму­ле F, если она получена из F заменой символов функций на сим­волы двойственных им функций.

Теорема (принцип двойственности.) Если формула F задает булеву функцию f(x₁, ...,x_n), то двойственная ей формула F* задает двойственную функцию f*(x₁, ...,x_n).

Пример. Рассмотрим формулу , задающую функ­цию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула должна задавать функцию, двойственную стрелке Пир­са - это штрих Шеффера: в самом деле - это функция НЕ-И, то есть штрих Шеффера.