8. Булева функция, способы ее задания.
Определение 1. Функцию f (x1, x2, ... , xn) называют булевой, если каждый ее аргумент есть булева переменная и сама функция — булева переменная.
Определение 2. Функцию f (x1, x2, ... , xn) называют булевой, если она сама и ее аргументы принимают значения 0 или 1.
Определение 3. Булевой функцией f (x1, x2, ... , xn) называют однозначное отображение булева пространства Bn в булево множество B, т.е. f: Bn B.
Пример. Рассмотрим булеву функцию двух аргументов, принимающую на наборах 01 и 10 значение 0, а на наборах 00 и 11 значение 1.
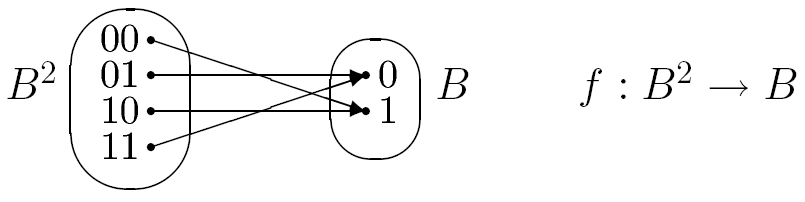
Способы задания булевых функций
1) Таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части пересчитываются все наборы значений аргументов (булевы векторы пространства Bn) в естественном порядке, т.е. по возрастанию значений чисел, представляемых этими векторами, а в первой части – значений булевой функции на соответствующих наборах.
Теорема
о числе булевых функций. Число
различных булевых функций, зависящих
от n
переменных, равно
.
2) Характеристическими множествами. Так называются два множества:
M1 (f), состоящее из всех наборов, на которых функция принимает значение 1, и M0 ( f ) — из всех наборов, на которых функция принимает значение 0, т.е.
M1 (f) = { B n : f () = 1}, M0 (f) = { B n : f () = 0}.
3) Вектором значений функции: (f) = f(0,0, ... ,0) f(0,0, ... ,1) ... f(1,1, ... ,1).
4) Матрицей Грея. Булево пространство задается матрицей Грея и наборами, на которых булева функция f(x1, x2, ... , xn) принимает значение 1, отмечаются и называются точками.
Пример.
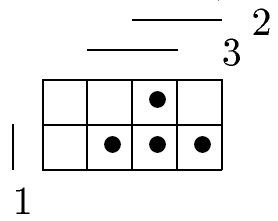
5) Интервальный способ задания. Булева функция f(x1, x2, ... , xn) задается множеством интервалов If={I1,I2,…,Ik}, объединение которых образует характеристическое множество M1(f) .
П
ример:
[Мажоритарная]
функция может быть задана достаточным
множеством If={I1,I2,I3}
интервалов:
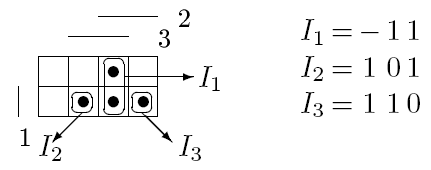
Здесь интервалы представлены троичными векторами и изображены на матрице Грея. В отличие от предыдущих, интервальный способ задания функций многовариантен.
6)
Формулами.
Пример.
9. Существенные и фиктивные переменные. Алгоритмы выявления и удаления фиктивной переменной.
Булева функция f(x1, x2, ... , xi , ... , xn) существенно зависит от переменной xi, если выполняется условие:
f (x1, x2, ... , xi -1, 0 , xi+1, ... , xn) f (x1, x2, ... , xi -1, 1 , xi+1, ... , xn).
В этом случае также говорят, что переменная xi существенная, в противном случае ее называют фиктивной переменной.
Пример. Рассмотрим булеву функцию f (x1, x2, x3) и исследуем ее переменные x1 и x3. Из таблиц истинности видно, что переменная x1 булевой функции f (x1, x2, x3) существенная, так как f (0, x2, x3) f (1, x2, x3). Переменная x3 фиктивная, так как f (x1, x2, 0) = f (x1, x2, 1).
Алгоритм выявления фиктивной переменной
- Для переменной x1 сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x1 = 0, а нижней x1 = 1; если они совпадают, то переменная x1 фиктивная;
- для переменной x2 сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x2 = 0, а в нижних x2 = 1; если четвертины в каждой половине совпадаю, то переменная x2 фиктивная;
- и так далее (за четвертинами следуют 1/8, 1/16, …).
Достаточное условие отсутствия фиктивных переменных. Если вес вектора – столбца значений функции нечетен, то функция не может содержать фиктивных переменных.
Алгоритм удаления фиктивной переменной xi состоит в вычеркивании из таблицы истинности всех строк, в которых xi = 0 (или всех строк, в которых xi = 1), и столбца xi .
Пример. После удаления фиктивной переменной x3 имеем
10. Формула как способ задания функции. Равносильные формулы. Основные равносильности
Пусть даны Ф — множество символов функций и Х — множество символов переменных.
База индукции. Если fi - символ n-местной функции из множества Ф, а x1, x2, ... , xn - переменные из множество Х, то последовательность символов fi (x1, x2, ... , xn) - формула над Ф и Х.
Индуктивный переход. Если fj - символ m-местной функции из Ф, а A1, A2, ... , Am — переменные из Х или формулы, то последовательность символов fj(A1, A2, ... , An) - формула над Ф и Х, а A1, A2, ... , Am – ее подформулы.
Других формул нет.
Способ записи формул для элементарных булевых функций: c a, b c , a и т.д.
Формула задает функцию, а функция реализует формулу.
Пример. ( a ( c a ) ) ( b c). или, если опустить скобки, то формула примет вид: a ca ( b c).