1. Булев вектор, длина булева вектора, теорема о числе булевых векторов, представление булевыми векторами подмножеств и натуральных чисел.

2. Булев вектор, расстояние между векторами, отношение предшествования.

3. Булево пространство, способы задания булева пространства.

4. Интервал в булевом пространстве, утверждение о мощности интервала, способы задания интервала.

5. Соседние интервалы. Утверждение о соседних интервалах.

6. Алгоритм распознавания интервала, заданного перечислением векторов.

7. Распознавание интервалов в матрице Грея. Типы интервалов.

8. Булева функция, способы ее задания.

9. Существенные и фиктивные переменные. Алгоритмы выявления и удаления фиктивной переменной.

10. Формула, как способ задания функции. Равносильные формулы. Основные равносильности.

11. Формула Шеннона. Доказательство.

12. Разложение функции по k переменным. Доказательство.

13. Получение СовДНФ из разложения функции по переменным. Утверждение о существовании и единственности СовДНФ. Алгоритм построения СовДНФ по таблице истинности функции.

14. Получение СовКНФ из разложения функции по переменным. Утверждение о существовании и единственности СовКНФ. Алгоритм построения СовКНФ по таблице истинности функции.

15. Двойственная функция и двойственная формула. Принцип двойственности.

16. Двойственная функция. Построение двойственной функции по таблице истинности.

17. Элементарная конъюнкция. Ортогональные, смежные и соседние конъюнкции.

18. Утверждение о конъюнкции и интервале. ДНФ и достаточное множество интервалов.

19. Импликанты и простые импликанты функции.

20. Сокращенная, кратчайшая, минимальная и безызбыточная ДНФ.

21. Метод Закревского получения приближенной кратчайшей ДНФ.

22. Поиск сокращенной ДНФ: теорема Квайна и алгоритм Квайна-МакКласки.

23. Поиск сокращенной ДНФ: теорема Блэйка и алгоритм Блэйка-Порецкого.

24. Поиск кратч. ДНФ с помощью таблицы Квайна. Алг-м поиска всех безызбыточных покрытий.

25. Поиск кратчайшей ДНФ с помощью таблицы Квайна. Алг-м поиска кратчайшего покрытия.

26. Частичные булевы функции, способы их задания, доопределение.

27. Частичные булевы функции, точный метод их минимизации.

28. Частичные булевы функции, их минимизация по матрицам в коде Грэя. Метод Закревского.

29. Метод конкурирующих интервалов для минимизации частичной булевой функции.

30. Система булевых функций. Кратчайшая и безызбыточная системы ДНФ.

31. Получение приближенной кратчайшей системы ДНФ методом конкурирующих интервалов.

32. Определение графа, орграфа, мультиграфа и псевдографа.

33. Степень вершины. Лемма Эйлера. Теорема о числе вершин нечетной степени.

34. Смежность вершин и ребер графа. Матрица смежности.

35. Инцидентность вершин и ребер графа. Матрица инцидентности.

36. Типы графов: пустой, полный, регулярный, двудольный.

37. Типы подграфов. Остовное дерево. Циклический ранг.

38. Изоморфизм графов.

39. Связность графа. Марщрут, цепь, простая цепь, цикл. Лемма о цепи.

40. Связность графа.Разделяющее множ-во, разрез, мост, точка сочленения. Лемма о точ-х сочленения.

41. Расстояние между вершинами графа. Диаметр, радиус и центр графа.

42. Теорема об оценке числа ребер в графе и следствие о связном графе.

43. Связность графов, односторонняя, сильная, слабая. Фактор граф.

44. Обход графа. Обход в глубину.

45. Обход графа. Обход в ширину.

46. Поиск кратчайших путей в орграфе. Волновой алгоритм.

47. Поиск минимальных путей в нагруженном графе. Алгоритм Дейкстры.

48. Теорема о шести эквивалентных утверждениях о дереве.

49. Задача о соединении городов. Алгоритм Краскала.

50. Эйлеровы циклы. Лемма о цикле. Теорема о необ-х и достаточных условиях эйлеровости графа.

51. Эйлеровы графы. Алгоритм Флери.

52. Гамильтоновы графы. Теорема Дирака.

53. Гамильтоновы графы. Задача коммивояжера и методы ее решения.

1. Булев вектор, длина и вес булева вектора, теорема о числе булевых векторов, представление булевыми векторами подмножеств и натуральных чисел.

Булевыми константами называют символы 0 и 1.

Булевым множеством называют множество булевых констант B = {0, 1}

Булев вектор это последовательность конечного числа булевых констант, называемых компонентами булева вектора.

Булев вектор обозначают греческими буквами, а компоненты вектора — латинскими с указанием номеров компонент.

Пример:   =  a₁ a₂ ... a_n  =  010101,    =  b₁ b₂ ... b_n  =  11110000 .

Длина булева вектора - количество его компонент

Вес вектора — количество компонент, равных единице.

Пример. Длина булева вектора  = 101010 равна шести, а вес — трем.

Теорема о числе булевых векторов:

Число различных булевых векторов длины   n   равно   2ⁿ .

Доказательство.

1. База индукции. При   n = 1  утверждение  выполняется  (число различных булевых векторов длины 1 равно двум: это 0 и 1).

2. Предположение. Пусть число различных булевых векторов длины   n равно   2ⁿ .

3. Вывод. К булевым векторам длины  n  добавим n +1- ю компоненту, присвоив ей сперва значение 0 (получим 2ⁿ векторов длины   n +1),  затем — значение 1 (получим еще  2ⁿ векторов длины   n +1),  т.е. всего 2ⁿ + 2ⁿ  = 2ⁿ⁺¹ различных векторов длины   n +1.

Примеры. Имеется 4 булевых вектора длины два:   00, 01, 10, 11, и 8 булевых векторов длины три: 000, 010, 100, 110, 001, 011, 101, 111.

Представление булевыми векторами подмножеств

Пусть заданы множество  M = {m₁, m₂, ... , m_n} и подмножество A  M. Построим булев вектор    = a₁ a₂ ... a_n, представляющий подмножество A, по следующему правилу:

 1, если m_i  A;

a_i = 

 0, если m_i  A.

Примеры. В множестве M = {2, 6, 4, 7, 8 } булев вектор  = 11101 выделяет подмножество четных чисел, булев вектор  = 10010 выделяет подмножество простых чисел.

Представление булевыми векторами целых неотрицательных чисел

Введем следующее соответствие между булевыми векторами длины n и числами  0, 1, ... , 2ⁿ -1: пусть булев вектор    = a₁ a₂ ... a_n соответствует числу

a  =   a_i  2^{n - i}

a_i принимает значение 0 или 1.

Пример. Задан булев вектор  = 1001; подставив его компоненты в формулу, получим число: a  =  12³   +  02²   +  02¹   +  12⁰  = 8 + 1 =  9.

2. Булев вектор, расстояние между булевыми векторами, отношение предшествования.

Булев вектор  — это последовательность конечного числа булевых констант, называемых компонентами булева вектора.

Булев вектор обозначают греческими буквами, а компоненты вектора — латинскими с указанием номеров компонент.

Пример:   =  a₁ a₂ ... a_n  =  010101,  

  =  b₁ b₂ ... b_n  =  11110000

Определение. Говорят, что булевы векторы  и    ортогональны по i‑й компоненте, если   a_i    b_i .

Расстоянием между булевыми векторами называют число ортогональных компонент в данной паре векторов (его еще называют расстоянием по Хэммингу).

Булевы векторы называются соседними, если они ортогональны по одной и только одной компоненте.

Булевы векторы называют противоположными (антиподами), если они ортогональны по всем компонентам.

Булев вектор  = a₁ a₂ ... a_n предшествует булеву вектору  = b₁ b₂ ... b_n   (обозначают     ), если для любого i = 1, 2, ... , n выполняется условие:   a_i    b_i . В этом случае также говорят, что булев вектор  следует за булевым вектором , булев вектор  называют предшественником, а  - последователем.

Пример. Расстояние по Хэммингу между булевыми векторами  = 1010 и  = 1001 равно двум.

Пример.  = 1010,  = 1110:   .  

3. Булево пространство, способы задания булева пространства.

Булевым пространством Bⁿ размерности  n  называется множество всех булевых векторов длины  n, расстояние между которыми вычисляется по Хэммингу.

1) Явным перечислением векторов.

Пример. B ³ = {000, 001, 010, 011, 100, 101, 110, 111}.

2) Матрицей в коде Грея. Булево пространство размерности n представляется матрицей, состоящей из 2^s строк и 2^p столбцов, где  s  и  p — целые числа, такие что  s + p = n и s = p либо s = p - 1. Строкам матрицы поставлены в соответствие булевы векторы длины s (их называют кодами строк), а столбцам — булевы векторы длины p (коды столбцов).

Элемент матрицы, стоящий в i – й строке и j – м столбце, задает булев вектор, который получается приписыванием к коду строки i кода столбца j.

Можно задавать матрицу в позиционном коде, или матрицей Грея.

Пример. Пусть n = 5. Тогда a = 2, b = 3, строк 2² = 4, столбцов 2³ = 8.

Выделенная клетка задает булев вектор 10011. На левой матрице показан процесс построения кодов столбцов.

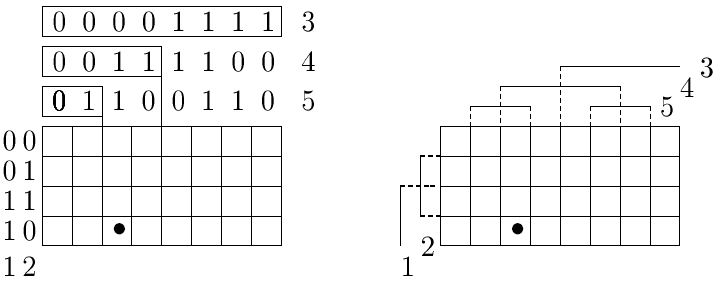
На правой матрице коды изображены условно: единица - черточкой, а ноль - ее отсутствием: такой код более нагляден, да и быстрее рисуется.

На правой матрице пунктирными линиями обозначены места смены значений компонент, эти линии называются осями симметрии компонент.

Нетрудно заметить, что пара соседних векторов располагается в матрице симметрично относительно оси той компоненты, по которой векторы ортогональны.

4. Интервал в булевом пространстве, утверждение о мощности интервала, способы задания интервала.

Пусть задана пара векторов одинаковой длины:   = a₁ a₂ ... a_n и   = b₁ b₂ ... b_n .

Интервалом I (,)  в булевом пространстве B ⁿ, заданным парой булевых векторов    и  , таких что   , называется множество всех булевых векторов    длины  n,   удовлетворяющих условию        , т.е. I (,) = {  Bⁿ :     }. Булевы векторы   и   называются границами интервала, вектор  - наименьшим элементом интервала, а  - наибольший элемент.

Пример. I (000,011) = {000, 001, 010, 011}.

Утверждение   о   мощности   интервала.

Мощность интервала размерности s равна 2^s .

Доказательство. Так как интервал состоит из булевых векторов со всевозможными комбинациями нулей и единиц во внутренних компонентах, а внутренние компоненты образуют булев вектор длины  s, то число таких векторов (Теорема о числе булевых векторов: Число различных булевых векторов длины   n   равно   2ⁿ) равно  2^s.

Определение. Компоненты, по которым границы (а значит и все векторы интервала) совпадают, называются внешними компонентами интервала, остальные – внутренними. Число внешних компонент называется рангом интервала (r), а число внутренних – его размерность (s).

Пример: Мощность интервала – 0 – равна 2² = 4, мощность интервала 101 равна 2⁰ = 1.

Способы задания интервалов

1) Границами  интервала.

I (000,101) = {000, 001, 100, 101}, граница  = 000 – наименьший элемент, граница  = 101 – наибольшим.

I (010, 010) =  010, границы интервала совпадают, значит он состоит из одного

булева вектора.

I (000, 111) =  - - - , интервал - все булево пространство  B³,

2) Явным перечислением всех векторов, образующих интервал.

3) Троичным вектором. 0  и  1  задают значения внешних компонент, а черточка внутренние компоненты.

Примеры.

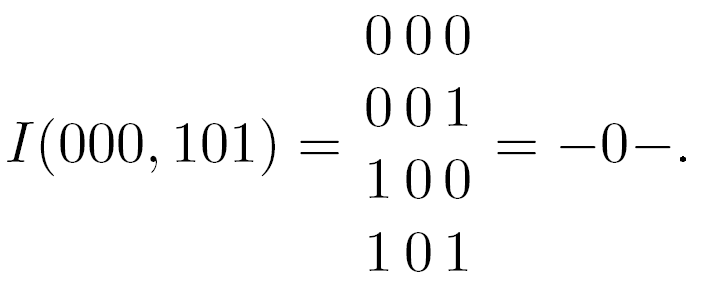
4) На матрице в коде Грея. Булево пространство представляется матрицей Грея, а все булевы векторы (клетки), образующие интервал, отмечаются. Все строки и все столбцы, коды которых совпадают с векторами интервала по внешним компонентам – на их пересечении и будет лежать интервал.

Примеры.