Билет 12.

1. Клики графа. Раскраски графов.

Клика — полный подграф неориентированного графа. Другими словами, клика графа есть подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большему подмножеству с тем же свойством.

На этом шаге мы рассмотрим раскраски графов.

Вершинной раскраской (далее - просто раскраской) графа называется отображение множества вершин графа на конечное множество (множество цветов); n-раскраска графа - раскраска с использованием n цветов. Раскраска называется правильной, если никакие две вершины одного цвета не смежны. Очевидно, что для графа без петель всегда существует правильная раскраска в |V| цветов. Хроматическим числом графа G называется минимальное число n=c(G), такое, что существует правильная n-раскраска.

2.???

Билет 13.

.

Билет 14.

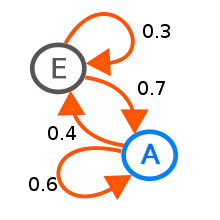
2. Вероятностный автомат — устройство или система, в которых переход из одного состояния в другое происходит в зависимости от случайных входных сигналов или в зависимости от последовательности предыдущих состояний.

Вероятностный автомат в основном используют в процессе обучения для демонстрации более сложного поведения, реакции которых сложно предсказуемы, например, систем автоматического управления движением транспорта на перекрестке двух улиц.

Цепь Маркова — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого.

Билет 15.

1. Примеры полных систем конечнозначных функций.

Конечнозначные логики (другое название — 'k'-значные) являются обобщением двузначной логики в том, что функция в ней может принимать не два значения (0 и 1), а значения от 0 до k−1. Существенным отличием 'k'-значной логики от двузначной является тот факт, что на данный момент не существует полного описания замкнутых классов при k>2. В двузначной логике напротив существует полное описание системы замкнутых классов, предложенное Эмилем Постом в 1940 году.

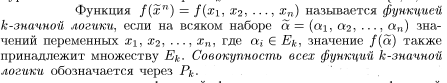
2..