Билет 11.

1.1 Эйлеров цикл и эйлеров граф. Условия существования эйлерова цикла. Задача о разбиении графа на минимальное число цепей.

Пусть 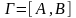- граф. Эйлеровым циклом в графе называется такой цикл, который содержит все ребра и все вершины этого графа. Напомним, что, по определению, в циклах не повторяются ребра. Таким образом, при наличии эйлерова цикла в графе этот граф можно обойти по всем ребрам, пройдя каждое ребро только один раз. Граф, обладающий эйлеровым циклом, сам называется эйлеровым.

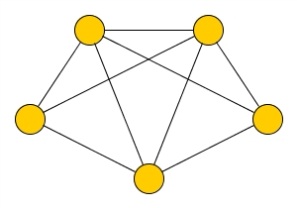
Вот пример эйлерова графа:

А вот пример графа, не являющегося эйлеровым:

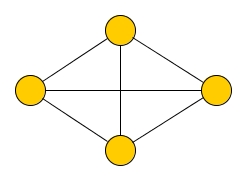
Существует теорема (теорема Эйлера), полностью описывающая эйлеровы графы:

Граф является эйлеровым тогда и только тогда, когда он связен и все его локальные степени четны.

Таким образом, имеется конкретный способ устанавливать, является или нет данный граф эйлеровым. Однако, если граф окажется эйлеровым, то указать его эйлеров цикл можно только после дополнительных исследований.

В связи с эйлеровыми графами имеется одна классическая задача о минимальном цепном разбиении. Вот ее формулировка.

Пусть - связный граф и - все его вершины нечетной степени (напомним, что в каждом графе число вершин нечетной степени четно). Тогда, если 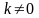, то минимальное число цепей графа, содержащих в совокупности все его ребра, равно ; если же , то указанное минимальное число равно 1.

В последней ситуации, указанной в этой формулировке, речь идет, очевидно, об эйлеровом графе. В первой же ситуации имеет смысл остановится на принципиальной схеме рассуждений. А именно: построим новый граф , в котором (т.е. добавляется одна новая вершина z) и 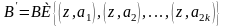(т.е. добавляется еще ребер); заметим, что полученный граф является связным и все его локальные степени уже четны; поэтому в нем существует некий эйлеров цикл ; осуществим обход по циклу , начав и закончив этот обход в вершине ; те цепей, о которых идет речь в обсуждаемом утверждении, будут выделяться в процессе этого обхода так: обход начинается в вершине ; следовательно, следующей за будет некая вершина из ; она и будет началом первой цепи; после некоторого пути надо будет вновь вернуться в ; первая цепь закончится в той вершине из , из которой осуществится возвращение в ; затем, продолжая движение по циклу C, вновь придется выйти из и снова выделится цепь в ; и так далее, пока не исчерпается весь цикл .

1.2 Гамильтонов цикл и гамильтонов граф. Условия Дирака, Оре и Поша, гарантирующие существование в графе гамильтонова цикла.

Пусть 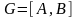- некоторый граф. Он называется гамильтоновым, если в нем существует простой цикл, содержащий все вершины графа. Например, каждый полный граф – гамильтонов, потому что в нем проведены всевозможные ребра и, в частности, те, благодаря которым возможен обход по всем вершинам. А вот пример графа, не являющегося гамильтоновым:

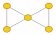
Общих и легко осуществляемых действий, с помощью которых можно было бы достоверно выяснить, является ли данный граф гамильтоновым, не существует. Однако, имеются достаточные условия на гамильтоновость, которые проверяются легко. Недостаток здесь состоит в том, что даже если ни одно из этих условий не выполняется, граф может оказаться гамильтоновым. В дальнейшем в этой лекции будет молчаливо предполагаться, что число вершин в любом рассматриваемом графе не меньше трех.

Итак, условие первое - условие Дирака. Пусть - число вершин в данном графе; если степень каждой вершины не меньше, чем , то граф называется графом Дирака. Можно доказать, что каждый граф Дирака обязательно гамильтонов.

Вот пример графа Дирака:

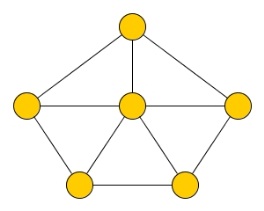
Очевидно, этот граф - гамильтонов. А вот пример гамильтонова графа, не являющегося графом Дирака:

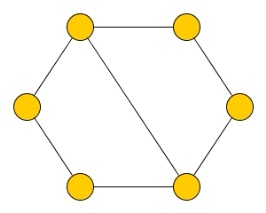
Условие второе - условие Оре. По-прежнему будем обозначать через количество вершин в данном графе. Если для любой пары несмежных вершин выполнено неравенство 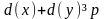, то граф называется графом Оре (словами: степени любых двух несмежных вершин не меньше общего числа вершин в графе). Можно доказать, что всякий граф Оре обязательно гамильтонов.

Вот пример графа Оре:

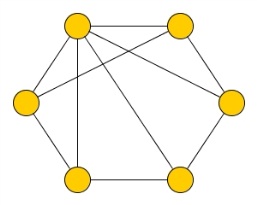
А вот пример графа, не являющегося графом Оре и, тем не менее, графа гамильтонова:

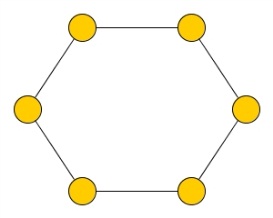
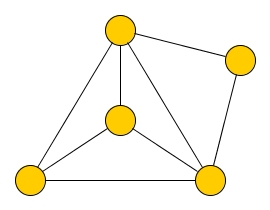
Нетрудно заметить, что всякий граф Дирака автоматически является графом Оре. Но вот пример графа Оре, не являющегося графом Дирака:

Условие третье - условие Поша. Это - более сложная конструкция. Введем следующую функцию целого неотрицательного аргумента . Сначала запишем определение формулой, а затем прокомментируем его. Итак, речь идет по-прежнему о графе , для которого и строится функция : ;

написанное означает, что функция в каждом целом неотрицательном принимает значение, равное количеству вершин графа , степень которых не превосходит . Такую функцию называют функцией Поша графа .

Для примера построим функцию Поша следующего графа:

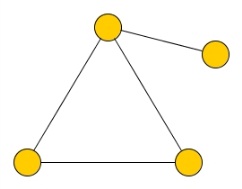
Функция будет описано таблично:

x	0	1	2	3	4	5	...
f(x)	0	1	3	4	4	4	...

Теперь сформулируем условие Поша.

Графом Поша называется граф , удовлетворяющий следующим условиям (число вершин этого графа обозначим через , его функцию Поша обозначим через , символ будет обозначать целое число):

1) для выполняется неравенство ;

2) если - целое число, то при имеет место неравенство: .

Можно доказать, что каждый граф Поша обязательно гамильтонов. Легко заметить, что простой цикл на большом числе вершин графом Поша не является, но, конечно, является гамильтоновым графом.

Кроме того, нетрудно заметить, что всякий граф Дирака является графом Поша. То же верно и в отношении графов Оре: каждый граф Оре является графом Поша. Обратное в обоих последних случаях неверно. Вот пример: фиксируем какой-нибудь полный граф на достаточно большом числе вершин; добавим к нему еще одну вершину и соединим ее с любыми двумя вершинами в исходном графе; очевидно, вновь полученный граф - гамильтонов; фиксируем в нем какой-нибудь гамильтонов цикл и удалим из графа какое-нибудь ребро, не включенное в этот цикл; полученный в результате граф будет, как нетрудно проверить, графом Поша; однако, он не будет графом Оре - будут сразу две пары несмежных вершин, сумма степеней которых меньше числа вершин в графе.