21. Условные распределения. Независимость случайных величин

Условное распределение  — это распределение  случайной величины при условии, что другая случайная величина принимает определённое значение

Будем предполагать, что задано вероятностное пространство .

Дискретные случайные величины

Пусть   и   — случайные величины, такие, что случайный вектор   имеет дискретное распределение, задаваемое функцией вероятности  . Пусть   такой, что  . Тогда функция

,

где   — функция вероятности случайной величины  , называется условной функцией вероятности случайной величины   при условии, что  . Распределение, задаваемое условной функцией вероятности, называется условным распределением.

Абсолютно непрерывные случайные величины

Пусть   и   — случайные величины, такие что случайный вектор   имеет абсолютно непрерывное распределение, задаваемое плотностью вероятности  . Пусть   таково, что  , где   — плотность случайной величины  . Тогда функция

называется условной плотностью вероятности случайной величины   при условии, что  . Распределение, задаваемое условной плотностью вероятности, называется условным распределением.

Свойства условных распределений

1. Условные функции вероятности и условные плотности вероятности являются функциями вероятности и плотностями вероятности соответственно, то есть они удовлетворяют всем необходимым условиям. В частности,

,

,

и

 почти всюду на  ,

,

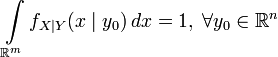2. Справедливы формулы полной вероятности

,

.

3. Если случайные величины   и   независимы, то условное распределение равно безусловному:

или

 почти всюду на  .

Условные математические ожидания Дискретные случайные величины

• Условное математическое ожидание случайной величины   при условии   получается суммированием относительно условного распределения:

.

• Условное математическое ожидание   при условии случайной величины   — это третья случайная величина  , задаваемая равенством

.

Абсолютно непрерывные случайные величины

• Условное математическое ожидание случайной величины   при условии   получается интегрированием относительно условного распределения:

.

• Условное математическое ожидание   при условии случайной величины   — это третья случайная величина  , задаваемая равенством

.

Независимость случайных величин

Случайная величина   называется независимой от случайной величины  , если закон распределения величины   не зависит от того, какое значение приняла величина  .

Для непрерывных случайных величин условие независимости   от   может быть записано в виде:

при любом  .

Напротив, в случае, если   зависит от  , то

.

Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.

Случайные величины   и   называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины   и   называются зависимыми.

Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид:

,                                                             

Определение 4. Случайные величины Х и У, определенные на одном и том же пространстве элементарных событий, называются независимыми, если для любых чисел а и b независимы события {X=a} и {Y=b}.

Утверждение 6. Если случайные величины Х и У независимы, а и b – некоторые числа, то случайные величины X+a и Y+b также независимы.

Действительно, события {X+a=с} и {Y+b=d} совпадают с событиями {X=с-a} и {Y=d-b} соответственно, а потому независимы.

Утверждение 7. Если случайные величины Х и У независимы, то математическое ожидание произведения ХУ равно произведению математических ожиданий Х и У, т.е. М(ХУ)=М(Х)М(У).

Два события называются независимыми если вероятность их совмещения ровна произведению вероятностей этих событий.

Несколько событий называются попарно независимыми если каждые два из них независимы.

Несколько событий называются независимыми в совокупности , если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных