Вопрос 14 Коэффициент корреляции и его использование в экономике
Корреля́ция(от лат. correlatio), (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.
Ковариация
Основные статьи: Ковариация, Неравенство Коши — Буняковского
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка. Ковариация определяется как математическое ожидание произведения отклонений случайных величин:
,
где
— математическое ожидание.
Свойства ковариации:
Ковариация двух
независимых случайных величин
и
равна нулю
Абсолютная величина
ковариации двух случайных величин и
не превышает среднего геометрического
их дисперсий:
В анализе экономических ситуаций расчет коэффициента корреляции имеет большое значение. В экономике, как правило, различные показатели связаны между собой стохастической (не строгой) связью. Часто экономисту приходится иметь дело со статистическими наблюдениями и делать по ним определенные выводы, давать объективные и обоснованные рекомендации. В таких ситуациях для моделирования поведения изучаемого объекта целесообразнее всего воспользоваться эконометрическим, в частности, корреляционным, подходом.
Вопрос 15 Простые и сложные индексы
В статистике под индексом (index) понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В связи с этим различают динамические, территориальные индексы, а также индексы выполнения плана. Многие общественные явления состоят из непосредственно не сопоставимых явлений, поэтому основной вопрос – это вопрос сопоставимости сравниваемых явлений. К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая величина). При исчислении важно правильно выбрать период, принимаемый за базу сравнения. Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.
Достижение в сложных статистических совокупностях сопоставимости разнородных единиц осуществляется введением в индексные отношения специальных сомножителей индексируемых величин. Такие сомножители называются соизмерителями. Они необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям. При этом в числителе и знаменателе общего индекса изменяется лишь значение индексируемой величины, а их соизмерители являются постоянными величинами.
В качестве соизмерителей индексируемых величин выступают тесно связанные с ними экономические показатели: цена, количество и др. Произведение каждой индексируемой величины на соизмеритель образует в индексном отношении определённые экономические категории.
Индивидуальные индексы
Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами.
Условные обозначения:
p – цена,
q – количество,
t – время,
T – численность,
f – з/п,
F – фонд з/п,
S – посевная площадь,
y – урожайность,
z – себестоимость.
Индекс получает название по названию индексируемой величины. В большинстве случаев в числителе стоит текущий уровень, а в знаменателе – базисный уровень. Исключением является индекс покупательной способности рубля. Индексы измеряются либо в виде процентов (%), либо в виде коэффициентов.
Сводные индексы
Сложные явления, для которых рассчитывается сводный индекс, отличаются той особенностью, что элементы, их составляющие, неоднородны и, как правило, несоизмеримы друг с другом. Поэтому сопоставление простых сумм этих элементов невозможно. Сопоставимость может быть достигнута различными способами:
сложные явления могут быть разбиты на такие простые элементы, которые в известной степени являются однородными;
сравнение по стоимости, без разбиения на отдельные элементы.
Цель теории индексов – изучение способов получения относительных величин, используемых для расчета общего изменения ряда разнородных явлений.
По охвату объекта различают индексы, характеризующие соотношение показателей по какому-нибудь отдельному элементу, и индексы, характеризующие соотношение показателей по сложной массе явлений, отдельные элементы которой не поддаются суммированию в силу того, что они разноименные и часто имеют разную единицу измерения.
Показатель, характеризующий соотношение явлений состоящих из разнородных элементов носит название общего (сводного) индекса и обозначается как - J. При этом, как правило, подстрочно дается значок, который указывает для оценки какой величины рассчитывается индекс. Например, общий индекс цен записывается следующим образом:
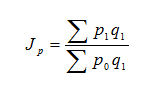
При вычислении общих индексов несоизмеримые элементы следует привести к соизмеримому виду. Приведение разнородных элементов к соизмеримому виду осуществляется с помощью специальных сомножителей, называемых весами-соизмерителями. Так, например, от натуральной формы продуктов переходят к денежной используя в качестве весов-соизмерителей цены или себестоимость.
Показатель, изменение которого изучается, называется индексируемой величиной. При этом, для того чтобы измерить изменение индексируемой величины, следует исключить влияние на величину индекса изменение веса, т.е. веса нужно брать на одном и том же уровне.
Если индексируемой величиной является качественный признак, то вес принимается на уровне текущего периода. Если же индексируемой величиной является количественный признак, то вес принимается на уровне базисного периода. Сводные индексы в агрегатной форме позволяют измерить не только относительное изменение отдельных элементов изучаемого явления в целом в текущем Основной формой общих индексов являются агрегатные индексы.
Расчет индексов по агрегатным формулам возможен, если есть полные данные о физическом объеме продукции и о ценах как на уровне отчетного так и базисного периодов. В реальной действительности полные данные имеются не всегда. В таких случаях приходится исчислять индексы как среднюю взвешенную величину из индивидуальных индексов. Средний из индивидуальных индексов будет тогда правильным, когда он тождественен агрегатному индексу. Это означает, что средние из индивидуальных индексов не самостоятельные индексы, а преобразованная форма агрегатного индекса. При исчислении средних индексов могут быть использованы только две формы средних: средняя арифметическая и средняя гармоническая: периоде по сравнению с базисным, но и абсолютное изменение.