Вопрос 11 Проверка гипотез
Проверки статистических гипотез — один из классов задач в математической статистике.
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина Х распределение которой Р известно полностью или частично. Тогда любое утверждение , касающееся Р называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
Статистическая гипотеза, однозначно определяющая распределение Р, то есть ,
где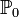
какой-то конкретный закон, называется
простой.Статистическая гипотеза, утверждающая принадлежность распределения
к некоторому семейству распределений,
то есть вида
, где
— семейство распределений, называется
сложной.
На практике обычно
требуется проверить какую-то конкретную
и как правило простую гипотезу
. Такую гипотезу принято называть
нулевой. При этом параллельно
рассматривается противоречащая ей
гипотеза
,
называемая конкурирующей или
альтернативной.
Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.
В большинстве случаев
статистические критерии основаны на
случайной выборке
фиксированного объема
из распределения
. В последовательном анализе выборка
формируется в ходе самого эксперимента
и потому её объем является случайной
величиной (см. Последовательный
статистический критерий).
Пусть дана независимая
выборка
из нормального распределения, где
— неизвестный параметр. Тогда
, где
— фиксированная константа, является
простой гипотезой, а конкурирующая с
ней
— сложной.
Этапы проверки статистических гипотез
Формулировка основной гипотезы и конкурирующей гипотезы . Гипотезы должны быть чётко формализованы в математических терминах.
Задание уровня значимости
,
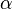на котором в дальнейшем и будет сделан
вывод о справедливости гипотезы. Он
равен вероятности допустить ошибку
первого рода.Расчёт статистики
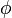критерия
такой, что:
её величина зависит от исходной выборки
;по её значению можно делать выводы об истинности гипотезы ;
сама статистика должна подчиняться какому-то известному закону распределения, так как сама является случайной в силу случайности
.
Построение критической области. Из области значений выделяется подмножество таких значений
,
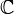по которым можно судить о существенных
расхождениях с предположением. Его
размер выбирается таким образом, чтобы
выполнялось равенство
. Это множество и называется критической
областью
.Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику и по попаданию (или непопаданию) в критическую область выносится решение об отвержении (или принятии) выдвинутой гипотезы .
Вопрос 12 Генеральная совокупность, выборка; виды выборок.
Генеральная совокупность, генеральная выборка (от лат. generis — общий, родовой)(в англ. терминологии — population) — совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.
Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность - это все население определённого региона (например, когда изучается отношение потенциальных избирателей к кандидату), чаще всего задаётся несколько критериев, определяющих объект исследования. Например, женщины 10-89 лет, использующие крем для рук определённых марок не реже раза в неделю, и имеющие доход не ниже $150 на одного члена семьи.
Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.
Характеристики выборки:
Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.
Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.
Необходимость выборки
Объект исследования очень обширный. Например, потребители продукции глобальной компании – огромное количество территориально разбросанных рынков.
Существует необходимость в сборе первичной информации.
Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30—35.
При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок:
пары близнецов,
два измерения какого-либо признака до и после экспериментального воздействия,
мужья и жёны и т. п.
В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например:
мужчины и женщины,
психологи и математики.
Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.
Сравнение выборок производится с помощью различных статистических критериев:
t-критерий Стьюдента
Критерий Уилкоксона
U-критерий Манна-Уитни
Критерий знаков
и др.
Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной.
Репрезентати́вность — соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом. Репрезентативность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана.
Также репрезентативность можно определить как свойство выборочной совокупности представлять параметры генеральной совокупности, значимые с точки зрения задач исследования.
Выборки делятся на два типа:
Вероятностные - использование такой выборки основывается на предположении
Невероятностные - отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.