1. При соединении “треугольник” фазное напряжение равно линейному напряжению .

Учитывая, что нагрузка симметричная, находим фазные токи:

2. Определяем линейные токи:

3. Активная мощность одной фазы

4. Активная мощность всей трёхфазной нагрузки:

5. Строим векторную диаграмму:

.

1. строим базис – тройку симметричных векторов фазных (они же линейные) напряжений , , . (См рис.11);

2. строим вектора фазных токов и под углом сдвига фаз к соответствующим векторам фазных напряжений в сторону отставания ;

3. на основании уравнений состояния в соответствии с первым

законом Кирхгофа строим вектора линейных токов

Рис.11

Задача 4.Данные и требования такие же, как и в задаче 3. Отличие в типе соединения: вместо треугольника соединение звезда. (рис.12 )

Рис.12

Решение

1. При соединении “звезда”

2. Фазные (они же линейные) токи определим на основании закона Ома

3. Фазная активная мощность

4. Активная мощность всей трёхфазной нагрузки

5. Векторная диаграмма

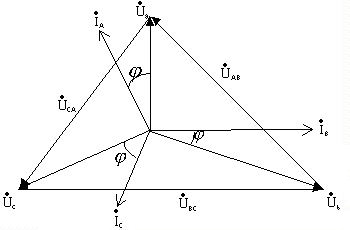
Рис. 13

а) строим базисную тройку векторов фазных напряжений ;

б) в сторону опережения по фазе ( нагрузка активно-ёмкостная ) под углом относительно соответствующих фазных напряжений строим вектора фазных (они же линейные) токов

Угол ;

в) на основании второго закона Кирхгофа вектора линейных напряжений найдем исходя из следующих уравнений:

Задача 5. В трехфазную четырехпроводную линию с симметричным линейным напряжением U включен электроприемник, собранный по схеме «звезда» (см. рис. 14). Даны сопротивления фаз

Рис. 14

Определить фазные и линейные токи, ток в нейтральном проводе, активную мощность всей цепи и каждой фазы в отдельности.

РЕШЕНИЕ

1. Благодаря наличию нейтрального провода напряжение на всех фазах симметризовано. Поэтому

2. Фазные токи (они же линейные)

3. Фазные активные мощности

, ,

4. Активная мощность всей трехфазной нагрузки

5. Ток в нейтральном проводе найдем графическим методом с помощью векторной диаграммы (Рис.15.):

Рис. 15

a) строим базисную тройку симметричных векторов фазных напряжений ,

под соответствующими углами сдвигов фаз строим вектора фазных (они же линейные)

токов, задавшись при этом определенным масштабом.

- вектор тока совпадает по фазе с вектором т.к. сопротивление фазы А чисто активное. Длина вектора определяется выбранным масштабом.

- вектор отстает по фазе от вектора на угол т.к. фаза В имеет активно-индуктивный характер сопротивления. Длина вектора определяется в соответствии с масштабом и отмеряется линейкой. Угол откладывается по транспортиру.

- вектор опережает на угол

б) строим вектор тока нейтрального провода , для этого складываем (с помощью

циркуля) вектора

(на основании первого закона Кирхгофа)

Замеряем линейкой длину вектора , умножаем её на масштаб и т.о. узнаем величину

тока .

Замечание:

Длину вектора (т.е. величину тока в нейтральном проводе) можно вычислить аналитически, используя законы геометрии. В этом случае диаграмма строится качественно (не в масштабе), а длина вектора вычисляется либо по проекциям, либо по теореме косинусов.