Логическая модель представления знаний.
Эта модель основана на логике предикатов (функция, принимающая значение 0 или 1) и булевой логике решения задач.
L = <T, P, А, F>
T – множество базовых элементов;
P – множество синтаксических правил, позволяющих строить из T правильные выражения;
А – множество аксиом, априорно истинных выражений.
F – семантические правила вывода, позволяющие расширять множество аксиом за счёт других выражений.
Каждый объект из предметной области M может быть экземпляром определенного класса k, относящегося к множеству К – множество всех классов, на которые могут быть разбиты объекты предметной области.
Каждому классу ставится в соответствие характеристическая функция, представляющая собой решающий предикат:
σk = 1, если m принадлежит k.
σk = 0, если m не принадлежит k.
Каждый объект может быть описан множеством признаков. Каждый признак, соответствующий определённому свойству объекту может быть представлен в следующем виде:
pi(m) = 1, если m обладает признаком pi.
pi(m) = 0, если m не обладает признаком pi.
Логическое описание объекта Zk(m) = конъюнкция (&i) всех признаков pi(m) , зарегистрированных на данном объекте.
Для логического описания класса составляется аксиома А(k) = дизъюнкция (Vd) всех логических описания класса Zjk(m).
Для распознавания объектов, то есть для определения того, к какому классу относится объект m, строится логическое решающие правило по следующему алгоритму:
На некотором шаге рассматривается логическое описание Zn и Zn-1 (на текущем и на предыдущем шаге).
К этому описанию добавляется признак pi и описание этого признака.
Для всех признаков объекта выбирается тот, при включении которого максимизируется апостериорная вероятность того, что объект m принадлежит k-му классу.
Таким образом, Zn стремится к характеристической функции класса: Zn σk. Решающее правило может быть представлено в виде бинарного графа признаков, в вершине которого находятся признаки, соответствующее максимальной апостериорной вероятности.
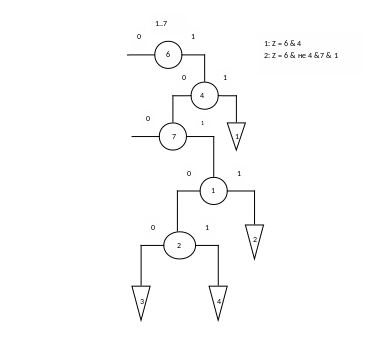
Для построения аксиомы класса аналогично на каждом шаге происходит добавление логического описания максимизирующего отнесения объекта к определённому классу. Аксиома будет учитывать возможные вариации логических описаний объектов класса.
Логическая модель представления знаний использует для решения задач метод резолюций. Этот метод известен как метод доказательства от обратного. Задача представляется в виде теоремы, такой что некоторая формула G следует из множества формул F. Доказательство теоремы состоит в том, чтобы показать несовместность множества G и отрицания F (пустое множество). При решении задачи отыскивается противоречие, затем противоречие преодолевается и приходим к новому множеству формул до достижения целевого условия.
Продукционные системы (модели).
Продукция – это правила переписывания или система подстановок, используемая для описания переходов пространства состояний из одного состояния в другое. С продукционными системами связано понятие лингвистических знаний, для описания которых используется теория формальных грамматик Хомского.
V – множество символов, называемых словарём или алфавитом. В качестве символов могут выступать буквы, геометрические образы, математические знаки и другие формальные объекты.
С – цепочка символов в словаре V. Это последовательность символов, образованной путём конкатенации. С = S1S2S3, Si принадлежит V. Множество всех цепочек в словаре V называется языком. Языки задаются грамматикой. Грамматика – это система правил, порождающая все цепочки языки и только их. Различают следующие виды формальных грамматик:
Распознающая. Определяет для каждой цепочки её принадлежность определённому классу.
Порождающая. Позволяет строить любые правильные цепочки языка.
Преобразующая грамматика. Позволяет получить для каждой цепочки её отображение в виде новой цепочки языка.
Любая грамматика состоит из следующих элементов:
G = <T, N, P, S >
T – терминальный словарь.
N – нетерминальный (вспомогательный) словарь.
P – множество правил продукции. Способ замещения цепочек одного вида цепочками другого вида. P: C S.
S – начальный символ или цель грамматики. Это предложение.
Словарь V представляется как объединение терминального и нетерминального словарей.
Построение фраз на естественном языке с использованием продукционной системы.
T = {датчик, образ, система, тактильный, визуальный, формировать, создавать, образ}
N = {Подлежащее, Сказуемое, О, Д}
N = {ГП, ГС}
S = {ПРедложение}
P |
S: ПР (ГП)(ГС) ГП (О)(П) ГС (C)(Д) П {система} О {тактильный, визуальный} С {формировать, создавать} Д {образ} |
ПР = (ГП)(ГС) = (О)(П)(С)(Д) = визуальный система формировать образ.
Можно добавить род и другие правила языка.
Системы представления знаний на основе продукционной системы.

БД – база данных рассматривается как динамическая система, изменяющая своё состояние под воздействием множества правил продукции, которые составляют БЗ – базу знаний. Стимулом для функционирования системы управления является различие между текущим состоянием базы данных и терминальным состоянием.
Продукционная система функционирует до тех пор, пока не дойдёт до терминального состояния или не остановится из-за отсутствия необходимой продукции.
Теория нечетких множеств.
Виды неопределенностей в электронном виде. Для отражения неопределенностей среды ученый Л. Заде предложил теорию нечетких множеств, 1982 и ввёл понятие лингвистической переменной, т.е. переменной, значение которой расплывчато по своей природе. Необходимость использования нечеткого подхода вызвана следующими обстоятельствами:
Для решения некоторых задач не нужна точная оценка параметров объектов и явлений. С ростом сложности системы способность человека делать точные и значащие утверждения относительно её поведения постепенно падает. В определённом пределе может быть достигнут порог, при котором точность и значимость являются взаимоисключающими понятиями. Нечеткие множества используются для описания нечетких отношений, нечетких алгоритмов и нечетких правил принятия решений.
Пример: Введем основные понятия.
A = {x1,x2,x3,x4,x5}.
B принадлежит A.
B = {x1,x3,x5}
Функция принадлежности μB(x) = 0, если x не принадлежит А, 1 если x принадлежит А.
B = {(x1|1),(x2|0),(x3|1),(x4|0),(x5|1)}
Вводится нечеткая мера принадлежности μB в интервале [0,1], которая называется мерой уверенности.
Экспертные оценки: B = {(x1|0,9),(x2|0,3),(x3|0,7),(x4|0,1),(x5|0,8)}, таким образом определили B как нечеткое подмножество множества А.
Лингвистическая переменная вводится: L = <F,T,U,C,S>, где
F – имя переменной (лингвистическое понятие).
T – множество термов, представляющих собой имена нечетких переменных, областью определения которых является множество принадлежности U.
U – универсальное множество из элементов которого образованы все множества переменной.
С – синтаксическая процедура, позволяющая образовывать из T новые осмысленные значения лингвистической переменной.
S – семантическая процедура, позволяющая приписать каждому новому значению переменной некоторую семантику путём формирования нечёткого множества.
Например, L = {скорость, (малая, средняя, высокая), [0..300], C, S}.
Малая – [0..100]
Средняя – [101..200]
Высокая – [201..300]
Основные операции.
Включение одного множества в другое. А принадлежит B, значит для всех x из множества X мера принадлежности x множеству А, должна быть меньше или равна мере принадлежности x к множеству B: μA(x)<=μB(x).
Равенство множеств. А=B. Для всех x из множества X меры уверенности должны быть равны: μА=μB.
Дополнение множеств. B=отрицание А. Для всех x из X вычисляем новые меру уверенности: μB=1-μА.
Пересечение множеств. Результатом является наибольшее нечёткое подмножество, содержащееся одновременно и в А и в B. μ=min(μА,μВ).
Объединение. Это наименьшее нечеткое подмножество, содержащее как А, так и В. μ=max(μА,μВ).
При применении нечёткой логики в графах для отношений между вершинами вводятся меры уверенности. Можно использовать нечеткие множества при формировании моделей нечётких нейронный сетей, где вводится понятие нечеткого нейрона.
При использовании в нечётких алгоритмах элементы перехода тоже берутся с мерой уверенности. Если ветвление, то не «да» или «нет», а «да» с мерой уверенности 0,3, а «нет» с мерой уверенности 0,7. Аналогично с циклом например, условие повторения или окончания цикла.
Также могут применяться в нечетких семантических сетях. Здесь нечеткими могут быть не только отношения между вершинами, но и сами значения вершин.
Моделирование речевого общения.
Преимущества речевого общения:
Удобство для человека.
Возможность обмена информацией сразу с несколькими источниками.
Возможность установления личности по голосу.
Управление на расстоянии.
Недостатки:
Может нарушаться секретность информации.
Чувствительность к искажениям звука.
Необходима настройка на диктора.
Осложняется работа при быстрой речи.
Речь – это звуковой сигнал, обладающий следующими характеристиками:
Основной тон. Определяет высоту звука. Чем выше частота, тем выше тон.
Тембр. Это характеристика звука, связанная с наличием высокочастотных составляющих, позволяющая различить звук одинакового основного тона от различных источников.
Амплитуда. Характеризует громкость звука. Слышимый диапазон: от 20 Гц до 20 КГц. Меньший диапазон – инфразвук, а выше – ультразвук.
Речевой сигнал представляет собой амплитудно-временную зависимость или осциллограмму. Для дискретизации непрерывного звукового сигнала используются временное квантование и амплитудная дискретизация.
Для анализа речевого сигнала рассматривается спектрограмма, которая показывает амплитуду по каждой частоте в каждый момент времени, это трёхмерная информация.
Существует два направления работы с речью: синтез речи и распознавание речи.
В основе синтеза естественного языкового сигнала находятся фонемы. Фонема – это элементарная смыслоразличительная частица языка. В каждом языке свое количество фонем. В русском языке 42 фонемы (6 – гласных, 36 согласных). В английском языке – 44 звука(фонемы) (20 гласных, 24 согласных).
Алафоны – это оттенки фонем, связанные с их соединением при произнесении. Различают комбинационные и позиционные. Позиционные связаны с позицией в слове по отношению к ударению, началу и концу слова, а комбинационные – с соединением звуков.
Дифоны – содержит переходную информацию от центра согласного к центру гласного и наоборот.
Для синтеза важны просодические характеристики речи. Это интонация и ударение.