Вопрос 63: Условия достижения общего равновесия.

Общим равновесием называется такое состояние, когда наблюдается равновесие всех рыночных субъектов и на всех рынках. Математически условие общего равновесия может быть записано так:

При этом первое равенство соответствует состоянию равновесия в экономике обмена, а второе – в экономике производства. Более подробно о состояниях равновесия в различных экономиках будет рассказано ниже, в ответах на соответствующие вопросы.

Вопрос 64: Общее равновесие и эффективность в обмене.

Обменная сделка

Проанализируем, как происходит обмен. Начнем с начального запаса товаров, обозначенного на рис.28.1 точкой W.

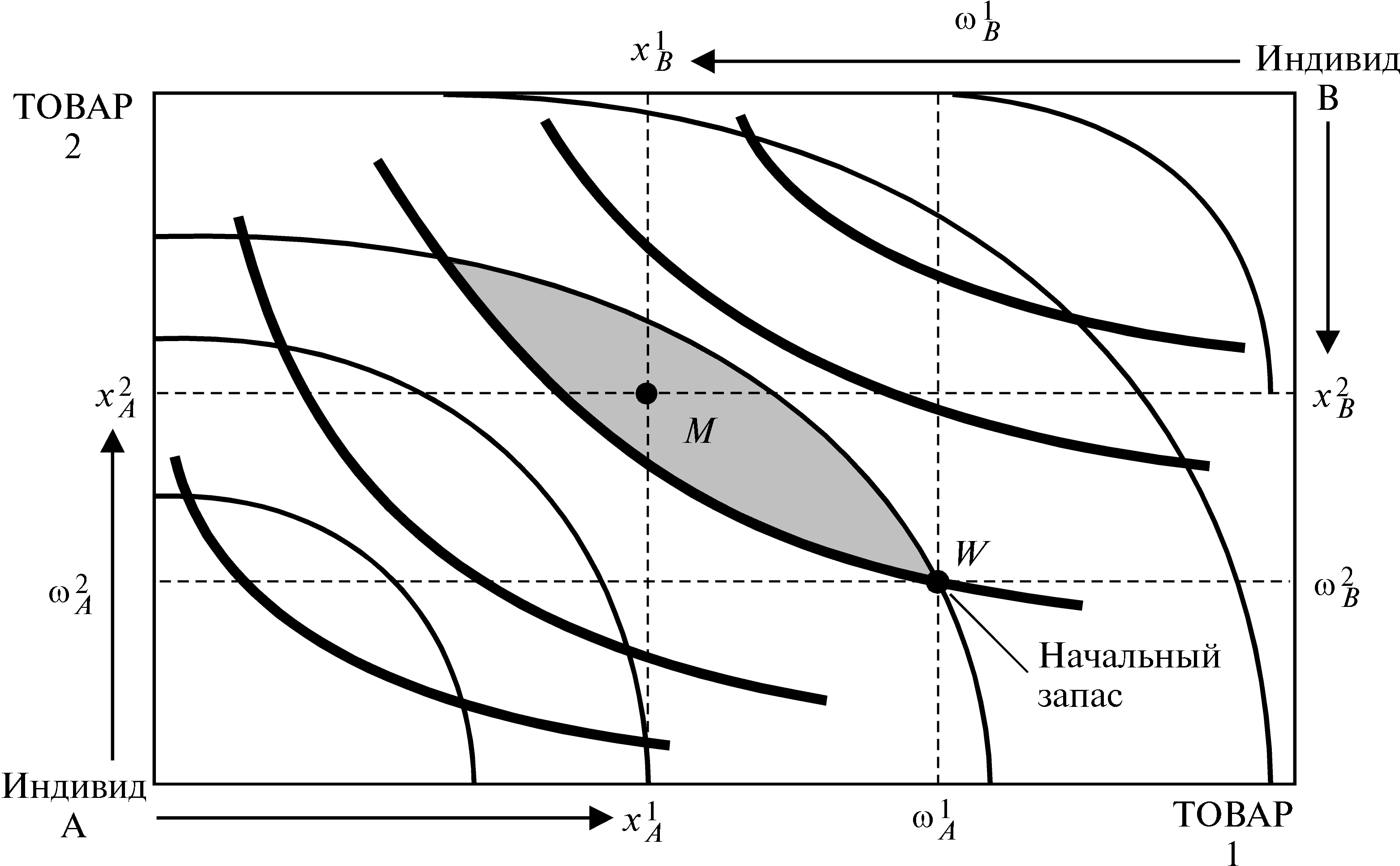
Рисунок 28.1 Ящик Эджуорта.

Рассмотрим кривые безразличия для A и B, проходящие через это распределение. Область, в которой благосостояние A выше, чем в точке его начального запаса, состоит из всех распределений, находящихся над его кривой безразличия, проходящей через точку начального запаса. Область, в которой благосостояние B выше, чем в точке его начального запаса, состоит из всех распределений, находящихся, с точки зрения B, над его кривой безразличия, проходящей через W. Где находится та область ящика, в которой выше благосостояние и A, и B? Ясно, что она находится на пересечении двух указанных областей. Это имеющая форму линзы область, показанная на рис.28.1. Предположительно в ходе переговоров двум участвующим в них людям удастся найти некую взаимовыгодную сделку, в результате которой они передвинутся в какую-то точку внутри линзообразной области, подобную точке M на рис.28.1.

Конкретное перемещение в точку M, изображенное на рис.28.1, подразумевает отказ индивида A от | — |276 единиц товара 1 и приобретение в обмен | — |277278 единиц товара 2. Это означает, что B приобретает | — |279280 товара 1 и отдает | — |281282283 единиц товара 2.

Теперь можно повторить тот же самый анализ применительно к точке M. Мы можем провести через M две кривые безразличия, построить новую линзообразную "область взаимной выгоды" и представить себе, что участники сделки премещаются в какую-то новую точку N, лежащую в этой области. Обмен будет продолжаться до тех пор, пока не исчерпаются сделки, предпочитаемые обеими сторонами.

Распределения, эффективные по Парето

Ответ на этот вопрос дан рис.28.2. В точке M данной диаграммы множество точек, располагающееся над кривой безразличия индивида A, не пересекает множества точек, располагающегося над кривой безразличия индивида B. Область, в которой благосостояние индивида A становится выше, отделена от области, в которой становится выше благосостояние индивида B. Это означает, что любое движение, повышающее благосостояние одной из сторон, с необходимостью понижает благосостояние другой. Таким образом, не существует обменных сделок, которые были бы выгодны для обеих сторон. При таком распределении взаимовыгодные сделки отсутствуют.

Распределение такого рода известно как распределение, эффективное по Парето. Распределение, эффективное по Парето, можно описать как такое распределение, при котором:

- не существует способа повысить благосостояние всех участвующих в обмене людей;

или

- не существует способа повысить благосостояние какого-либо индивида без понижения благосостояния кого-то другого;

или

- все выгоды от обмена исчерпаны;

или

- отсутствует возможность совершения взаимовыгодных сделок и т.д.

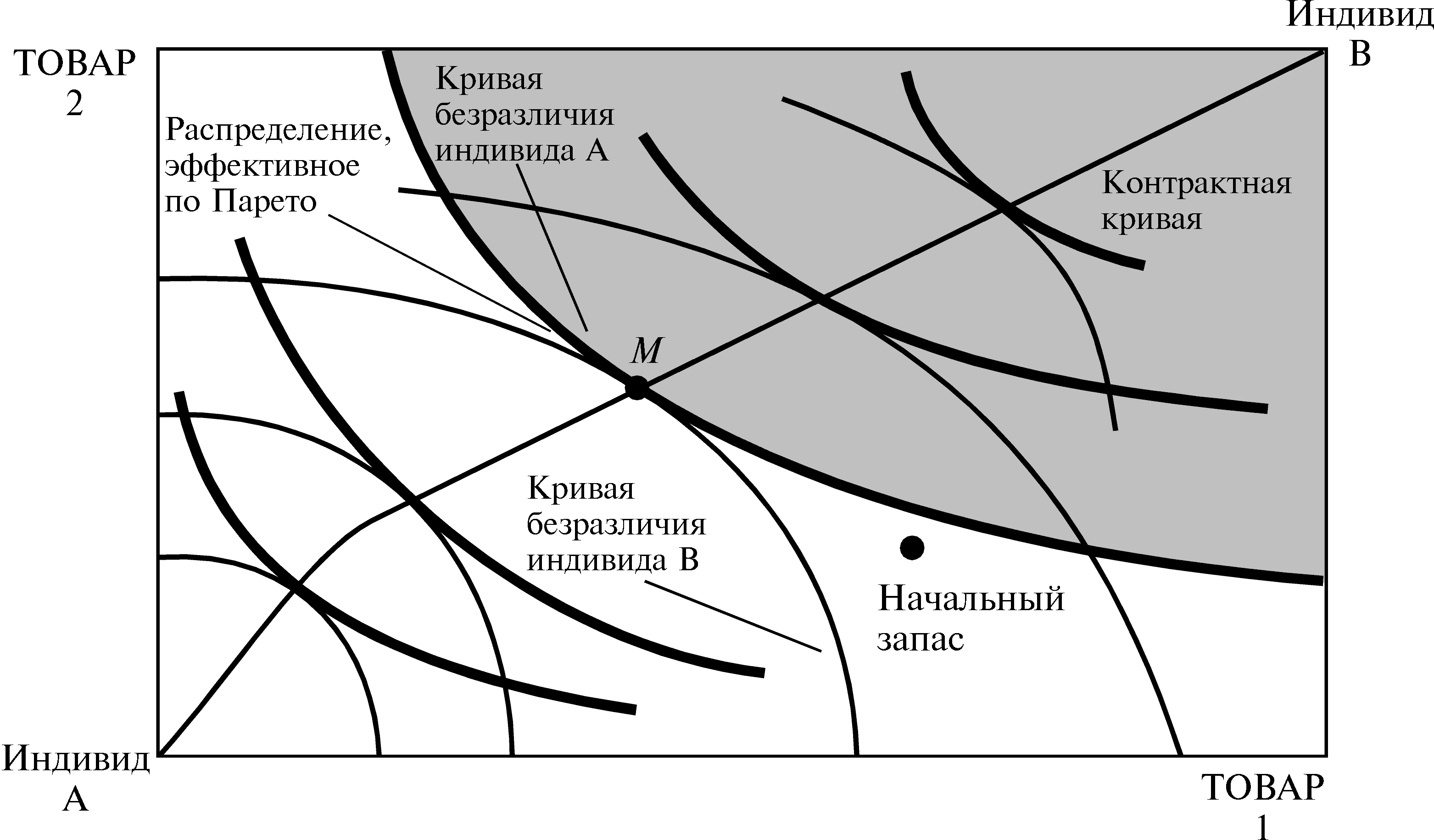
Рисунок 28.2 Распределение, эффективное по Парето.

Кривые безразличия двух участников обмена при любом эффективном по Парето распределении в ящике Эджуорта должны касаться друг друга. Почему это так, увидеть нетрудно. Если две кривые безразличия не касаются друг друга в точке распределения внутри ящика Эджуорта, значит, они должны пересекаться. Но если они пересекаются, то должна существовать возможность совершения взаимовыгодной сделки — поэтому данная точка не может быть эффективной по Парето. Из условия касания легко увидеть, что в ящике Эджуорта существует много распределений, эффективных по Парето. Фактически, если дана, например, любая кривая безразличия для индивида A, существует простой способ найти распределение, эффективное по Парето. Просто двигайтесь вдоль кривой безразличия для индивида A до тех пор, пока не найдете точку, являющуюся наилучшей для индивида B. Это и будет точка распределения, эффективного по Парето, и, следовательно, в ней обе кривые безразличия будут касаться друг друга.

Множество всех точек распределений, эффективных по Парето, в ящике Эджуорта называется множеством Парето, или контрактной кривой. В типичном случае контрактная кривая проходит от начала координат для A до начала координат для B через весь ящик Эджуорта, как показано на рис.28.2. Начнем движение из начала координат для A: в этой точке у индивида A нет ничего, все товары принадлежат индивиду B. Это распределение эффективно по Парето, поскольку единственный способ, которым можно повысить благосостояние A, состоит в том, чтобы отнять что-то у B. По мере движения вверх по контрактной кривой благосостояние A все больше растет, пока мы не доберемся, наконец, в начало координат для B.

Множество Парето описывает все возможные исходы взаимовыгодного обмена, независимо от того, в какой точке ящика мы начинаем движение. Если нам задана исходная точка, т.е. заданы начальные запасы для каждого потребителя, можно рассмотреть такое подмножество множества Парето, которое каждый из потребителей предпочтет своему начальному запасу. Это просто то подмножество множества Парето, которое лежит в линзообразной области, изображенной на рис.28.1. Распределения, находящиеся в этой линзообразной области, являются возможными исходами взаимного обмена, начинающегося с конкретного начального запаса, представленного на этой диаграмме. Однако само множество Парето не зависит от начального запаса, за исключением того обстоятельства, что начальный запас определяет общие наличные количества обоих товаров и тем самым размеры ящика.