Круглые валы.

Когда в поперечном сечении бруса равен нулю только один внутренний силовой фактор – продольная сила  , такой вид деформации называют изгибом с кручением.Изгибу с кручением подвергаются валы различных видов механических передач (ременные, зубчатые и т.д.).Например, воздействие ролика звена цепи на зуб шестерни цепной передачи (рис.2.7.1.) будет способствовать возникновению в произвольном поперечном сечении вала пяти внутренних силовых факторов:  ,  ,  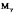,  ,  . В данном случае можно сказать, что вал испытывает деформацию изгиба с кручением.При изгибе с кручением в поперечном сечении возникают нормальные напряжения от изгиба в двух плоскостях, а так же касательные напряжения от кручения и изгиба.Для расчета вала в первую очередь необходимо установить опасные сечения. Для этого строят эпюры изгибающих моментов и крутящего момента, предварительно разложив нагрузки на составляющие вдоль координатных осей (рис. 2.7.2)Изгиб вала круглого и кольцевого поперечного сечения под действием изгибающих моментов   и   можно привести к прямому изгибу под действием результирующего (суммарного) изгибающего момента (рис. 2.7.3, а)

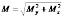 (2.7.1)

Вектор момента М в разных сечениях может иметь различные направления, в силу чего даже при отсутствии распределенных нагрузок эпюра М может быть криволинейной. Но при построении эпюры М обычно несколько завышают значения суммарного изгибающего момента, делая данные эпюры прямолинейными. Вычисляются значения суммарных моментов лишь для тех сечений, где на эпюрах   и (или)   есть переломы. Эти величины откладывают в масштабе по одну сторону от оси на эпюре М и соединяют прямой линией.

После построений эпюр суммарных изгибающих моментов и крутящих моментов определяют опасное сечение.

Опасной точкой в сечении вала круглого или кольцевого поперечного сечения, очевидно, будет точка, наиболее удаленная от центра сечения (рис. 2.7.3, б). В данной точке одновременно и нормальное напряжение от изгиба и касательное напряжение от кручения имеет наибольшее значение

;

У наиболее опасной точки выделим элемент (рис. 2.7.4, а). По четырем граням данного элемента действуют касательные напряжения, а к двум из этих граней приложены еще и нормальные напряжения. Остальные две грани свободны от напряжения. Таким образом, при изгибе с кручением элемент в опасной точке находится в пло Заметим, что в данном случае сложного напряженного состояния влиянием касательных напряжений от поперечных сил пренебрегаем, так как они значительно меньше касательных напряжений, вызванных кручением.

Для проверки прочности элемента, выделенного у опасной точки, нужно, выбрав соответствующую теорию прочности, сравнить значение эквивалентного напряжения с допускаемым для данного материала. Например, по четвертой теории прочности

 (2.7.2)

или, учитывая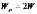 

 (2.7.3)

Выражение в числителе представляет собой приведенный момент, действие которого эквивалентно совместному действию трех моментов (согласно принятой теории прочности).

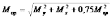 (2.7.4)

Теперь условие прочности можно заменить простой формулой

 (2.7.5)

При проектировочном расчете валов круглого поперечного сечения пользуются зависимостью полученной из условия прочности (2.7.5)

 (2.7.6)