64. Свертка и преобразование Фурье

Свёртка фу́нкций — операция, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. В математике, свёртка — это математическая операция двух функций f и g, порождающая третью функцию, которая обычно может рассматриваться как модифицированная версия одной из первоначальных. По существу, это особый вид интегрального преобразования. Результат свёртки показывает в каких местах один сигнал похож на другой, а в каких непохож.

Пусть   — две функции, интегрируемые относительно меры Лебега на пространстве  . Тогда их свёрткой называется функция  , определенная формулой

В частности, при   формула принимает вид:

Свёртка   определена при почти всех   и интегрируема.

Свойства

• Коммутативность: .

• Ассоциативность: .

• Линейность (дистрибутивность и умножение на число):

.

• Правило дифференцирования: ,

где   обозначает производную функции   по любой переменной.

• Свойство Фурье-образа: ,

где   обозначает преобразование Фурье функции  .

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции   вещественной переменной является интегральным и задаётся следующей формулой:

Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

60. Преобразование Фурье

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.Преобразование Фурье функции   вещественной переменной является интегральным и задаётся следующей формулой:

Свойства

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса  , преобразование Фурье может быть определено и для более широкого класса функций и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

• Преобразование Фурье является линейным оператором:

• Справедливо равенство Парсеваля: если  , то преобразование Фурье сохраняет  -норму:

Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство  . Равенство Парсеваля будет при этом справедливо для всех  .

• Формула обращения:

справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция   является достаточно гладкой. Если  , то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний   с частотами  , амплитудами   и фазовыми сдвигами   соответственно.

• Теорема о свёртке: если  , тогда

, где

Эта формула может быть распространена и на случай обобщённых функций.

• Преобразование Фурье и дифференцирование. Если  , то

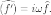
Из этой формулы легко выводится формула для  -й производной:

Формулы верны и в случае обобщённых функций.

• Преобразование Фурье и сдвиг.

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией  , а дифференцирование — свёртка с производной дельта-функции.

• Преобразование Фурье и растяжение.

• Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство  . Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции   её преобразованием Фурье называется обобщённая функция  , действующая на основные функции по правилу

Например, вычислим преобразование Фурье дельта-функции:

Таким образом, преобразованием Фурье дельта-функции является константа  .