3.3.2. Матриця суміжності

Нехай G = (V, Е) — простий граф, │v│ =п. Припустимо, що вершини графа G занумеровані: v₁ v₂, -, v„. Матрицею суміжності графа G (яка відповідає даній нумерації вершин) називають булеву п×п матрицю А з елементами a_ij (i,j= 1,..., п), де

Приклад 3.16. Матриця суміжності для графа, зображеного на рис. 3.14, має вигляд

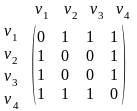
Цілком очевидно, що для неорієнтованого графа a_ij = a_ji, тобто матриця суміжності симетрична. Більше того, позаяк у простому графі немає петель, то для нього в матриці суміжності a_ii = 0 (I = 1, ..., п).

Матрицю суміжності можна використовувати також для подання псевдографа. Тоді це не булева матриця: елемент а_ij дорівнює кількості ребер, що з'єднують v_t та v_j. Петлю у вершині v_i подають значенням діагонального елемента а_й = 1. Для подання орієнтованих графів також використовують матрицю суміжності. Це булева п×п матриця А з елементами а_ij (i,j= 1, ..., п), де

Приклад 3.17. Матриця суміжності для графа, зображеного на рис. 3.15, має вигляд.

Зазначимо, що матриця суміжності орієнтованого графа, загалом кажучи, несиметрична.

Матрицю суміжності можна використовувати й для подання орієнтованого мультиграфа. У такому разі це не булева матриця: елемент a_ij дорівнює кількості дуг, які мають v_i початковою вершиною, а v_j — кінцевою.

Велика перевага матриці суміжності як способу подання графа — швидкий доступ до інформації: за один крок можна одержати відповідь на питання, чи існує ребро (дуга) з v_i y v_j. Вада полягає в тому, що незалежно від кількості ребер обсяг пам'яті становить п² комірок. Як іще один аргумент проти використання матриці суміжності можна навести теорему про кількість кроків алгоритму, який на основі матриці суміжності перевіряє якусь властивість простого графа (див. підрозділ 3.5, теорему 3.9).

Нарешті, розглянемо ще два способи подання графів у пам'яті комп'ютера. Будь-яку скінченну послідовність довільних елементів будемо називати списком, а кількість елементів списку — його довжиною.

3.3.3. Подання графа списком пар (списком ребер)

Метод зображення графа списком пар, які відповідають його ребрам (або дугам), значно економніший щодо пам'яті, особливо якщо т (кількість ребер) значно менша, ніж п² (п — кількість вершин). Пара [и, v] відповідає ребру {и, v}, якщо граф неорієнтований, і дузі (и, v), якщо граф орієнтований. Для графів, зображених на рис. 3.14 та 3.15, списки пар подані відповідно на рис. 3.16, а та 3.16, б.

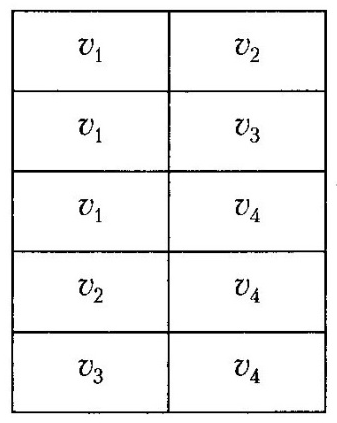
Рис. 3.15 Матриця суміжності неорієнтованого графу

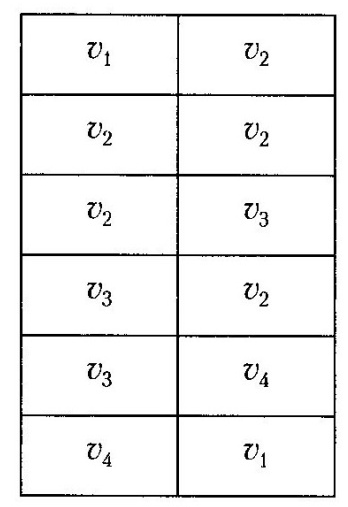
Рис. 3.16. Матриця суміжності орієнтованого графу

Очевидно, що обсяг пам'яті в цьому разі дорівнює 2т (т — кількість ребер або дуг). Це найекономніший щодо пам'яті спосіб. Його вада — велика (порядку п_і) кількість кроків для знаходження множини вершин, до яких ідуть ребра чи дуги із заданої вершини. Ситуацію можна значно поліпшити, упорядкувавши множину пар лексикографічно та застосувавши двійковий пошук.

3.3.4. Подання графа списками суміжності

Орієнтований граф G (без кратних дуг, але, можливо, з петлями) можна подати, зазначивши скінченну не порожню множину вершин V та відповідність Г, котра показує, як зв'язані між собою вершини. Відповідність Г — багатозначне відображення множини V у V. Граф у такому разі позначають парою G = (V, Г). У літературі часто означають (орієнтований) граф саме в таких поняттях [19, 20].