Основные понятия регрессионного и корреляционного анализа.
Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами называется корреляционным анализом. Основная задача корреляционного анализа – это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) показателями (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов.Характер связи между показателями определяется по корреляционному полю. Если Y – зависимый признак, а Х – независимый, то отметив каждый случай X(i) с координатами xi и yi получим корреляционное поле.
Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы. Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае, если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от – 0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полной ее отсутствии.
Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.
Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна.
Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности, точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию) – линию регрессии.
По числу факторов различают одно-, двух – и многофакторные уравнения регрессии. По характеру связи однофакторные уравнения регрессии подразделяются на: а) линейные, б) степенные в) показательные и др
Нахождение параметров линейного уравнения регрессии методом наименьших квадратов.
Уравнение регрессии записывается как
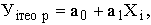
где Уiтеор – рассчитанное выравненное значение результативного признака после подстановки в уравнение X.
Параметры а0 и а1 оцениваются с помощью процедур, наибольшее распространение из которых получил метод наименьших квадратов. Его суть заключается в том, что наилучшие оценки ag и а, получают, когда
т.е. сумма квадратов отклонений эмпирических значений зависимой переменной от вычисленных по уравнению регрессии должна быть минимальной. Сумма квадратов отклонений является функцией параметров а0 и а1. Ее минимизация осуществляется решением системы уравнений
Коэффициент линейной корреляции и его свойства.
Практически для количественной оценки тесноты связи широко используют линейный коэффициент корреляции. Иногда его называют просто коэффициентом корреляции. Если заданы значения переменных Х и У, то он вычисляется по формуле
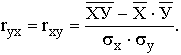
Можно использовать и другие формулы, но результат должен быть одинаковым для всех вариантов расчета.
Свойства коэффициента корреляции:
1. Коэффициент корреляции может принимать значения в интервале от -1 до +1 и равен +1 или -1 тогда, и только тогда, когда все точки диаграммы лежат на прямой линии, т. е. в этом случае имеем функциональную зависимость. Принято считать, что если |r| < 0,30, то связь слабая; при |r| = (0,3÷0,7) – средняя; при |r| > 0,70 – сильная, или тесная. Когда |r| = 1 – связь функциональная. Если же r принимает значение около 0, то это дает основание говорить об отсутствии линейной связи между У и X. Однако в этом случае возможно нелинейное взаимодействие. что требует дополнительной проверки и других измерителей
2. Линейные преобразования, сводящиеся к изменению масштаба или начала отсчета случайных величин Х и У, не изменяют значения коэффициента корреляции
3. Коэффициент корреляции между независимыми случайными величинами Х и Y равен нулю. Обратное утверждение неверно, т. е. из равенства нулю коэффициента корреляции не следует независимость случайных величин Х и Y. Если r(X,Y) = 0, то Х и Y называются некоррелированными.
Только в одном случае некоррелированность случайных величин влечет их независимость. Это имеет место, если Х и Y распределены по нормальному закону.