1. Предмет и метод теории вероятностей.

Теория вероятностей – математическая наука, изучающая закономерности в явлениях и опытах, результаты которых не могут быть заранее предсказаны: случайные события, случайные величины, их свойства и операции над ними.

Опыт, или эксперимент, - осуществление комплекса условий или действий, при которых происходят соответствующие явления.

Событие – возможный результат опыта (принято обозначать заглавными латинскими буквами). Исходы - различные результаты эксперимента.

Достоверное событие - (его также обозначают буквой Ω) – это событие, которое происходит всегда в данном опыте.

Невозможное событие (его обозначают как ∅)– событие, которое никогда не произойдет в данном опыте.

Случайное событие - любой факт, который в результате испытания может произойти или

не произойти.

Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей- служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей.

В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.

2. Случайные события, их классификация. Действия над событиями.

Случайное событие - любой факт, который в результате испытания может произойти или не произойти. Случайные события в зависимости от того, как они могут

появиться в испытаниях, классифицируются на:

единственно возможные (при испытании появление одного и только одного из них есть событие достоверное).

равновозможные (наступление одного из них не является более возможным, чем

другое).

несовместные (наступление одного из них исключает наступление другого). Если же появление одного из них не исключает возможность появления другого, то такие события называются совместными.

Два события называются противоположными, если появление одного из них равносильно не появлению другого.

Полной группой событий Ω называется совокупность событий, которые:

1) попарно несовместны;

2) в результате данного опыта происходит одно и только одно из них.

Операции (действия над событиями):

1. Сумма (объединение) двух событий А и В (обозначается A+B или А∪B) -событие, состоящее в появлении хотя бы одного из них.

2. Произведение (пересечение) двух событий А и В - событие, состоящее в их одновременном появлении.

3. Разность событий А и В есть событие, состоящее из исходов, входящих в А но не входящих в В.

Свойства операций над событиями:

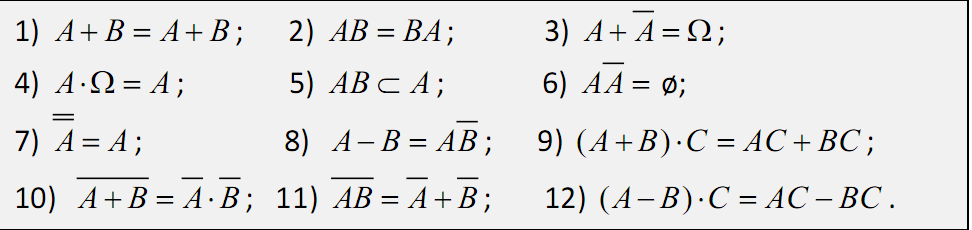
3. Классическое, статистическое и геометрическое определение вероятности.

1. Классической схемой, или схемой случаев, называется испытание, при котором число элементарных исходов конечно и все из них равновозможны.

Элементарное событие (исход) ω называется благоприятствующим событию А, если его появление влечет наступление события А (т.е. ω входит в число элементов, составляющих А).

Классической вероятностью события А называется отношение числа m элементарных событий, благоприятствующих событию А, к числу n всех равновозможных исходов опыта. .

Из определения вероятности следует, что Р (Ø) = 0, и .

2. Недостаток классического определения вероятности состоит в том, что это определение предполагает, что число событий является конечным числом. Однако существует множество экспериментов, где число исходов бесконечно. В этих случаях полезно использовать геометрические вероятности.

Геометрическое определение вероятности может быть использовано в том случае, когда вероятность попадания случайной точки в любую часть области пропорциональна мере этой области (длине, площади, объему и т.д.) и не зависит от ее расположения и формы.

Если геометрическая мера всей области равна S, а геометрическая мера части этой области, попадание в которую благоприятствует данному событию, есть , то вероятность события равна . Области могут иметь любое число измерений.

3. Статистическое определение вероятности: при рассмотрении результатов отдельных испытаний очень трудно найти какие-либо закономерности. Однако в последовательности одинаковых испытаний можно обнаружить устойчивость некоторых средних характеристик. Частостью какого-либо события в данной серии из n испытаний называется отношение m/n, числа m тех испытаний, в которых событие А наступило, к общему числу испытаний n. Почти в каждой достаточно длинной серии испытаний частость события А устанавливается около определенного значения , которое принимается за вероятность события А. Устойчивость значения частости подтверждается специальными экспериментами. Статистические закономерности такого рода были впервые обнаружены на примере азартных игр, т. е. на примере тех испытаний, которые характеризуются равновозможностью исходов. Это открыло путь для статистического подхода к численному определению вероятности, когда нарушается условие симметрии эксперимента. Частость события А называют статистической вероятностью, которая обозначается

где mA - число экспериментов, в которых появилось событие А;

n - общее число экспериментов.

Формулы классической вероятности и статистической имеют внешнее сходство, но они различны по существу. Формула КВ служит для теоретического вычисления вероятности события по заданным условиям опыта. Формула СВ служит для экспериментального определения частости события. Чтобы воспользоваться формулой СВ необходим опытный статистический материал.

4. Элементы комбинаторики: размещения, перестановки и сочетания.

Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных подмножеств, обладающих заданными свойствами, можно выбрать из данного множества.

Размещения. Размещениями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.Число размещений из n элементов по m в каждом обозначается символом и вычисляется по формуле , где (считается, что 0! = 1).

Размещения с повторениями. Каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов, взятых из данных n элементов.

Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.

Число размещений с повторениями из n элементов по m элементов обозначается символом и вычисляется по формуле

Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Число сочетаний из n элементов по m в каждом обозначается символом и вычисляется по формуле ,где .

Сочетания с повторениями. Сочетание с повторениями из n элементов по m элементов может содержать любой элемент сколько угодно раз от 1 до m включительно или не содержать его совсем, т.е. каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но из m каких угодно и как угодно повторяющихся элементов.Число сочетаний с повторениями из n элементов по m обозначают символом и вычисляют по формуле . В сочетаниях с повторениями m может быть и больше n.

Перестановки. Перестановками из n элементов называются такие соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.Число перестановок из n элементов обозначается символом , это то же самое, что число размещений из n элементов по n в каждом, поэтому . Перестановки с повторениями. Пусть имеются n элементов, среди которых элементов одного типа, элементов другого типа, элементовl-го типа . Число перестановок из этих n элементов равно числу перестановок с повторениями, обозначается и вычисляется по формуле

.