Локальные свойства непрерывности функций.

Th.1 Еслиf:ER непрерывна в точке аЕ, предельной точке Е, тоU(a;E): |f(x)|M(0;+)

x U(a;E), т.е. функция в этой окрестности ограничена.

Доказательсво сразу следует из определения непрерывности 

Th.1Пустьf:ER и :ER непрерывные в точке аЕ, предельной для Е. Тогда f(x)+(x),

f(x)*(x), f(x)/(x) (если(x)0) являются непрерывными в точке а.

(последнего) lim_Eэха[f(x)/g(x)]=(lim_Eэхаf(x))/( lim_Eэхаg(x))=f(a)/g(a) (g(a)0) эти теоремы выражают локальные свойства

Def.4 Функция, определеннапя следующим образом:

D(x) 1,xQ – множество рациональных чисел;

0, xR\Q=I –множество иррациональных чисел

D(x) – функция Дирихле. Функция Дирихле отображает R в R. D:RR. aR, покажем, что функция Дирихле в этой точке разрывна и докажем, что она всюду определена и всюду разрывна.

 _{a R}

( |)lim_хаD(x)  (предел не существует) 

^U(a)

Классификация точек разрыва функции.

Def.1Точка а называетсяточкой разрыва функцииf:ER первого рода, если f(a+0) f(a-0),

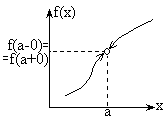
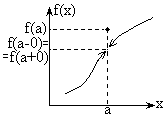Если хотябы один из этих пределов, то точка разрыва а называется точкой разрыва

второго рода. Другими словами точка разрыва второгго рода – все точки разрыва, которые не являются точками разрыва первого рода.

Def.2Точка разрыва первого рода называется точкой устранимого

разрыва, если f(a+0)=f(a-0) (предел слева равен пределу справа)

Если точка а есть точка устранимого разрыва, то достаточно измениить

функцию в одной лишь точке а, положив f(a)=lim_Eэхаf(x)= f(a+0)=f(a-0),

чтобы эта новая функция была уже непрерывна в точке а.

Def.3Разрыв первого рода назыывается разрывом первого рода типа конечного скачка

функции f, еслиh(a):= f(a+0)-f(a-0). (h(a) – скачок функции в точке а) Функция Дирихле имеет в каждой точке разрыв 2-ого рода, так как  f(a+0) иf(a-0)

Пример f(x)=1/x ; a=0 f(0+0)=+ ; f(0-0)=-, а-точка разрыва 2-ого рода

Свойства функций, непрерывных на отрезке. Глобальные свойства нерерывных функций.

Th.1 (Больцано-Коши о промежуточном значении) fc[a,b] и f(a)*f(b)<0c[a,b]:f(c)=0

I₀=[a,b] Разделим пополам точкой (a+b)/2 на 2

отрезка [a,(a+b)/2],[(a+b)/2,b] Еслиf((a+b)/2)0, тогда

выберем такой отрезок, на коцах которого функция

принимает значения разного знака и обозначим этот

отрезок I₁; I₁I₀. Поступим с отрезкомI₁ точно также

как и с отрезком I₀ и получим отрезок I₂ и так далее

I₂I_1. На некотором этапе получим либо на конце отрезка значение, равное 0, либо этого не

происходит и мы получам систему стягивающихся отрезков. По лемме о стягивающейся системе

отрезках  точка сI_n n=0,1,2… в точке с функция непрерывнаI_n=[ x_n’;x_n”] lim_n

x_n’=c=lim_n x_n”, построению отрезкаI_nf(x_n”)*f(x_n’)<0(перейдем в этом неравенстве к

пределам)  lim_n(f(x_n’)*f(x_n”))= =lim_nf(x_n’)*lim_nf(x_n”)=f(c)*f(c)= f(c)²<0  f(c)=0

Следствие (из теоремы Больцано Коши).

Пусть функцияf(х) непрерывна на интервале (c,d). Точки a,b(c,d), тогда:l, расположенном

междуA= f(a) иB= f(b) x_орасположеная расположенная между точкамиa и b:f(x_о)=l

f(x)=C[a,b](множество функций, непрерывных на[a,b])ктакой функции применима теорема Б.-К. Рассмотрим:(х):=f(x)-lC[a,b], т.к.f(x) C[a,b] (по теореме онепрерывных функций)

(a)=f(a)-l=A-l (b)=f(b)-l=B-lУмножим(а)*(b)=(A-l)*(B-l)<0, т.к.lлежит между А и Водна из скобок будет отрицательной. Из теоремы Б.-К.:  x_о(a,b):( x_о)=0 ; ( x_о)=0=f(x_о)-l f(x_о)=l 

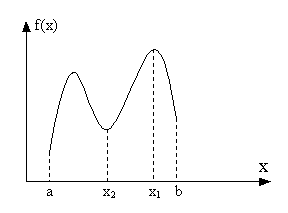
Th.1 (Вейерштрасса о достижении точных граней)

Пусть функция f:[a,b]R: fC[a,b] Тогда справедливы 2 утверждения:

1) f(x) – ограничена на[a,b] (т.е. М(0;+): |f(x)|M x[a,b])

2) точные верхние и нижние грани достигаются функциейf(x)на отрезке[a,b], т.е.

x₁[a,b]:=sup_x[a,b]f(x₁)=f(x) (*) иx₂[a,b]:=inf_x[a,b]f(x)=f(x₂) (**)

 1) Предположим противное, т.е. что f(x)не ограничена на[a,b]

Обозначим I₀:=[a,b]поделим его пополам, тогда хотябы в одном из этих 2-х отрезков функция не ограничена.Обозначим I₁ тототрезок, на котором функция не ограничена (I₁ I_о).ПоделимI₁пополам, и обозначимI₂ один из этих 2-х отрезков, где функция не ограничена (I₂ I₁). Получаем последовательность стягивающихся отрезковI_n …  I₂ I₁ I_o по лемме о стягивающихся отрезках! x_oI_n nN/{0}Эта точка обладает следующим свойством:веё окрестности функция не ограничена иx_o[a,b], но в точкеx_of(х) непрерывна и lim_{[a,b]эxxo}f(x)=f(x_o)>0=()>0 |x- x_o|<, x[a,b]| f(x)-f(x_o)|< 

-< f(x)-f(x_o)< ; f(x_o)-< f(x) < f(x_o)+  функция ограничена, а мы предположили обратное  противоречие 

2) Докажем (*) Предположим, что (*) не выполнено  А:=sup_x[a,b]f(x)>f(x) x[a,b]. Рассмотрим(х)=A-f(x)C[a,b] ; (x)>0 x[a,b].Рассмотрим(x)=1/(x)=1/(A-f(x)), т.к. нет точки разрыва (знаменатель не обращается в 0)(x)C[a,b]по первой части теоремы(x)ограничена (во всяком случае сверху) некоторой константой В(0;+), т.е. 1/(A-f(x))B x[a,b] A-f(x)1/b  f(x)A-1/B x[a,b]. Это означает, что A-1/B является мажорантой множества значений функции f(x) на отрезке [a,b], но по определению точной верхней грани число А является самой маленькой из множества мажорант, но А-1/В<А, что невозможнопротиворечие получено

Формула (**) доказывается аналогично 

ЗамечаниеТеорема Вейерштрасса перестает быть верной, еслиfC[a,b]

Пример f(x)=1/x