Правила составления уравнений по мун

Со знаком «+» в уравнение по МУН записывается узловое напряжение того узла, относительно которого составляется уравнение, все остальные – со знаком «».

Задающие токи источников ЭДС и тока берутся со знаком «+», если направление источников ориентированно к узлу, относительно которого составляется уравнение, и со знаком «»  если от узла.

При наличии в схеме ветви с идеальным источником ЭДС необходимо принять за опорный узел один из узлов к которому присоединена данная ветвь. Тогда узловое напряжение другого узла будет равным величине ЭДС.

Порядок расчета по мун

1.     Определяется число уравнений;

2.     Выбирается опорный узел;

3.     Составляется и решается система уравнений по МУН;

4.     По закону Ома определяются токи ветвей.

 

Пример: Для цепи рис 2.8 составить уравнения по МУН и определить токи ветвей.

 

 

 

 

 

 

 

 

 

 

Рис. 2.8

Решение:

Примем U₃ = 0;

 

 

 

 

 

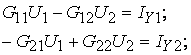
Токи ветвей определяются по закону Ома через найденные значения узловых напряжений:

 

 

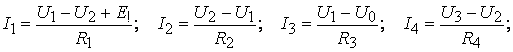
2.5. Вопросы для самоконтроля к лекции 2

 

1.     Какие напряжения и токи называются постоянными?

2.     Каков порядок расчета цепи постоянного тока?

3.     Какими методами можно рассчитать резистивную цепь?

4.     Укажите порядок расчета электрической цепи методом контурных токов. Как выполняется расчет токов ветвей этим методом?

5.     Укажите порядок расчета электрической цепи методом узловых напряжений

6.     Как определяются токи ветвей по известным узловым напряжениям?

7.     Разберите решения задач 1.38, 1.39, 1.41, 1.42,1.44 из [4]

8.     Решите задачи 1.40, 1.45 из [4].

 

Литература: [1] с. 63-72; [2] c. 26-31; [3] c. 82-88; [4] c. 8-12; [5] c. 71-75.

 

Лекция 3. ЛЭЦ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

 

3.1. Гармонические колебания и их описание

 

Электромагнитный процесс в ЭЦ, при котором мгновенные значения напряжения и токов повторяются через равные промежутки времени, называются периодическим.

Периодический процесс называется гармоническим, если функция f(t) (напряжение, ЭДС, ток) изменяется по закону синуса

 

f(t) = A_m sin(t +);                                       (3.1)

u = U_m sin(t +_U);    e = E_m sin(t +_e);    i = Im sin(t =_i)

 

Значения u, e, i, в любой момент времени называются мгновенными значениями.

Наибольшее по абсолютному значению отклонение колеблющейся величины называется ее амплитудой   .

Наименьшее значение времени, после которого процесс полностью повторяется, называется периодом колебания Т.

Число циклов колебаний в единицу времени называется циклической частотой   .

Число циклов колебаний в интервале времени равному 2 единицам, называется угловой частотой  .

Величина   называется фазой колебания. Она характеризует состояние колебания в любой момент времени t.

Значение фазы колебания в момент времени t=0 называется начальной фазой   . Начальная фаза является алгебраической величиной. При  начало синусоиды сдвинуто влево, а при   - вправо от начала координат.

 

 

 

 

 

 

 

 

 

 

 

Рис. 3.1.

 

3.2. Действующее значение периодической функции

 

Действующим значением любой периодической функции называют ее среднеквадратичное значение за период.

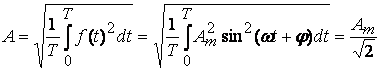.                      (3.2)

Действующее значение синусоидального тока или напряжения в   раз меньше его амплитуды

                        (3.3)

Действующее значение периодического синусоидального тока равно по величине такому постоянному току, который, проходя через сопротивление R за интервал времени Т, выделит такое же количество тепла, что  и данный периодический ток

                                              (3.4)

Большинство измерительных приборов показывают действующее значение тока и напряжения.

 

3.3. Представление гармонических колебаний векторами

 

Для непосредственного сложения синусоидальных функций необходимо производить достаточно громоздкие операции. Существенное упрощение достигается, если синусоидальную функцию изобразить в виде вращающегося вектора.

Векторное изображение синусоиды строится следующим образом (см. рис. 3.2).

 

 

 

 

 

 

 

 

Рис. 3.2.

 

На плоскости из начала координат под углом  , равному начальной фазе синусоиды, проводится прямая и на ней откладывается в масштабе отрезок, равный амплитуде колебания. Угол   откладывается против часовой стрелки от горизонтальной оси, если  ; и по часовой стрелке, если  . Если угол  откладывать от горизонтальной оси, то проекция вектора на вертикальную ось равна (в выбранном масштабе) мгновенному значению синусоидальной функции.

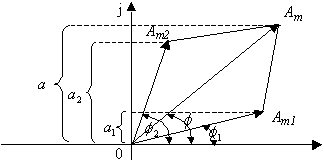
Построим векторное изображение суммы двух функций (рис. 3.3):

 

                               (3.5)

 

Очевидно, что вместо сложения синусоид удобно геометрически складывать их векторные изображения. Таким образом, получили простейшую векторную диаграмму.

 

 

 

 

 

 

 

 

 

Рис. 3.3.

 

Векторная диаграмма представляет собой совокупность векторов, изображающих синусоидальные функции одинаковой частоты, построенных с соблюдением масштаба и правильной ориентации их друг относительно друга по фазе.

Условились: вместо амплитуд на векторных диаграммах откладывать действующее значение функции.

 

3.4. Связь между мгновенными значениями напряжения и тока на элементах цепи