8.2. Переходная и импульсная характеристики

 

Переходной характеристикой h(t) называется реакция цепи на воздействие в форме единичной ступенчатой функции 1(t).

Импульсной характеристикой g(t) называется реакция цепи в форме единичной импульсной функции  (t).

Операторная передаточная функция и переходная и импульсная характеристики связаны между собой:

 

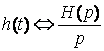; g(t) H(p)                                      (8.4)

 

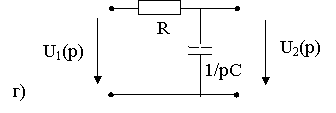
Пример: Определить переходную и импульсную характеристики цепи (рис. 8.2а)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 8.2.

 

Расчёт можно произвести тремя методами:

1.     Классический метод расчёта (рис. 8.2, б)

u_C(0)=0; u_C(t)=u_Cпр+u_Cсв; u_Cпр=Е;

 

;

 

; при t=0 u_C(0)=E+A=0A=-E;

;

.

 

2.      Операторный метод расчёта.

Эквивалентная операторная схема приведена на рис. 8.2, в

 

;

;

 

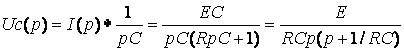3.     С помощью операторной передаточной функции (рис. 8.2г)

 

;

 

.

 

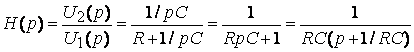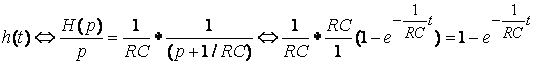8.3. Временной метод анализа лэц

 

Временной метод анализа применяется для определения реакции цепи на сложное воздействие при нулевых начальных условиях. Использование понятий переходной и импульсной характеристик позволяет свести расчёт реакции цепи на сложное воздействие к определению реакции на простейшее воздействие типа единичной 1(t) или импульсной функции (t), с помощью которых аппроксимируется исходное воздействие. При этом результирующая реакция находится как сумма реакций цепи на элементарные воздействия.

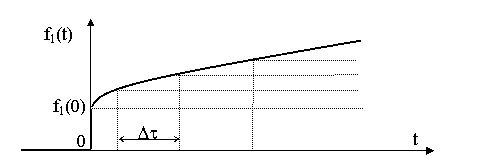
Если известна переходная характеристика цепи, то сложное воздействие f₁(t) аппроксимируется ступенчатыми функциями, возникающими через равные промежутки времени  (рис. 8.3)

 

 

 

 

 

 

 

 

 

Рис. 8.3 Представление сложной функции ступенчатой функцией.

 

В этом случае реакция цепи определяется при помощи интеграла Дюамеля.

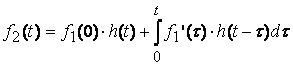                     (8.5)

 

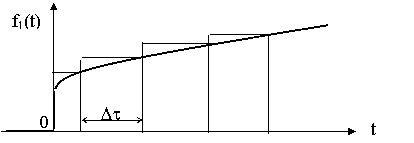
Если известна  или легко определяется импульсная характеристика цепи, то сложное воздействие f₁(t) аппроксимируется последовательностью прямоугольных импульсов (рис. 8.4)

 

 

 

 

 

 

 

 

 

Рис. 8.4. Представление сложной функции последовательностью прямоугольных импульсов.

 

В этом случае реакция цепи f₂(t) определяется при помощи интеграла наложения.

.                                  (8.6)

 

Расчёт ЭЦ временным методом производится в следующем порядке:

1.     Определение переходной h(t) или импульсной g(t) характеристики цепи.

2.     Определение переходной h(t-) или импульсной g(t-) характеристики путём замены t на t-.

3.     Определение производной от входного напряжения u₁(t) по времени.

4.     Определение реакции с помощью интеграла Дюамеля или наложения.

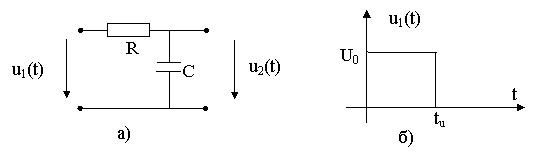
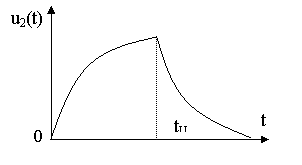
Пример: Определить u₂(t) цепи рис. 8.5.

 

 

 

 

 

 

 

 

Рис. 8.5. Исходная схема а) и вид воздействия б).

;

u₁(0)=U;  ; u₁’()=U₀’=0;

При  0 t  t_U

.

При t  t_U

             .

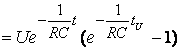Рис. 8.6. Временная зависимость выходного напряжения.