Движение газа в каналах с большой скоростью

Основные формулы адиабатического течения

При движении газа с большими скоростями (обычно выше 150 м/сек) в потоке возникают большие перепады давлений в результате чего плотность газа может сильно измениться. Изменение плотности в свою очередь влияет на скорость, что делает невозможным применение к замам методов расчета несжимаемых жидкостей.

Основным уравнением для расчета одномерного газа является уравнение энергии движущегося газа выведенное нами ранее и полученное на его основе уравнение Бернулли. В большинстве задач газовой динамики изменение удельной потенциальной энергии g(z₂-z₁) мало по сравнению с изменением кинетической энергии 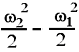, поэтому второй член в уравнении Бернулли для газа, который нельзя считать несжимаемым полагают равным нулю. В результате оно принимает вид:

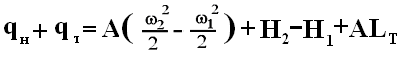
или в механической форме:

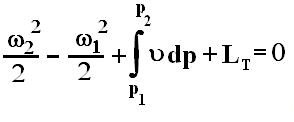
Встречающиеся на практике случаи течения с высокими скоростями обычно не сопровождаются существенным теплообменом газа с окружающей средой, потому теплообменом на единицу массы газа можно пренебречь и считать течение адиабатным (q_м=0). Теплота, выделяющаяся при трении равна работе трения q_т=Ah_т. В результате получается уравнение энергии для адиабатического течения:

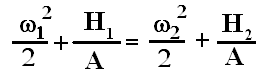
Так как H=c_pT (вспоминаем из курса химии) при адиабатном течении с возрастанием скорости газ охлаждается, а с уменьшением – разогревается. Учитывая также, что c_p/с_v=k и что pV/T=MR, можно энтальпию выразить через механические величины. Для этого выполним некоторые преобразования.

1. pV=MRT; p=M/V۰RT=ρRT; отсюда T=p/ρR

2. Из курса химии вспоминаем ещё одно уравнение: C_p=C_v+ AR и решаем его совместно с уравнением C_p/C_v=k:

C_p/C_v=1+AR/C_v; k=1+AR/C_v; k-1=AR/C_v; C_v=AR/(k-1); С_з/k=AR/(k-1);

Окончательно получаем C_p=k/(k-1)۰AR

3. Подставляем полученные выражения в уравнение энергии для адиабатического течения:

w₁²/2+1/A۰C_pT₁= w₂²/2 + 1/A۰C_pT₂;

+w₁²/2 +1/A۰k/(k-1)۰AR۰p₁/ρ₁R= w₂²/2 +1/A۰k/(k-1)۰AR۰p₂/ρ₂R

В итоге получаем;

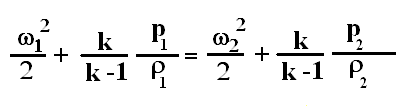
Уравнение энергии в вышеприведенной форме связывают скорость с плотностью и давлением газа, аналогично уравнению Бернулли для несжимаемой жидкости.

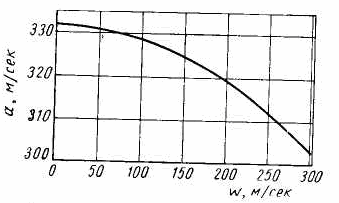
Как мы отмечали ранее, скорость звука связана со сжимаемостью среды, в которой он распространяется (a²=dp/dρ). Учитывая, что p/ρ=a^2//k (см. предыдущие лекции), преобразуем уравнение энергии;

w₁²/2+a₁²/(k-1) = w₂²/2+ a₂²/(k-1)

Если w₂=0, получаем w₁²/2+a₁²/(k-1) = a₂²(k-1)

Введём обозначения: a₁=a – скорость звука в потоке; w₁=w – скорость газа; a₂=a₀ – скорость звука в неподвижной среде. Тогда зависимость скорости звука в газе от скорости его течения описывается уравнением:

Рис 10

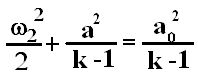
Если ω=0, то a=a₀. Следовательно, при ускорении потока скорость звука уменьшается (рис.10).

В некотором сечении потока скорость газа может стать равной скорости звука в том же сечении:

ω=a_*

Скорость потока, равная местной скорости звука, называется критической скоростью, а все параметры газа с критической скоростью –критическими параметрами.

В газовой динамике широко используют число Маха, представляющее собой отношение скорости потока к местной скорости звука:

и коэффициент скорости, представляющий собой отношение скорости потока к критической скорости:

λ'=ώ/a_*

Поток, скорость которого меньше местной скорости звука (ω <a, м<1) называется дозвуковым. При ω= a_* и м=1 течение называется звуковым или критическим. При ω> a_* (м>1) течение называется сверхзвуковым.

Следует отметить, что газовый поток можно ускорить лишь до определенного предела. Максимальная скорость достигается при истичении газа в вакуум, причем величина ее определяется из выражения:

ώ_макс= a_*√2/(k-1)