Свойства жидкостей и газов

Более подробно изучать явления переноса удобнее в газах, поэтому именно с них мы и начнем. Прежде всего, сформулируем несколько важных понятий.

Плотность- это отношение массы газа к занимаемому им объему:

Из закона Авогадро следует, что

, где

μ^* - молекулярная масса, [кмоль] (следствие закона Авогадро: при нормальных условиях 1моль любого газа занимает объем, равный 22,4л. Этот объем называется молярным объемом. Не путать с химическим потенциалом).

Коэффициент объемного расширения β – относительное увеличение объема при нагреве тела на 1градус.

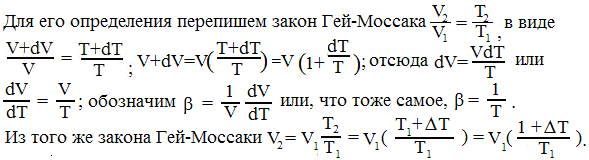
Если Т₁=273К (0°С), то V₂=V₁(1+βt) или, окончательно можно написать:

V_t=V₀(1+βt).

В соответствии с законом Бойля-Мариотта:

P₀V₀=P_tV_t.

несложные преобразования приводят к соотношению:

Давление есть сила, действующая на единицу площади. В газе и жидкости сила давления направлена нормально к поверхности элементарной площадки независимо от ориентации последней. Следовательно, давление является скаляром. Различают абсолютное и избыточное давление. Избыточное давление представляет собой разницу между давлением в какой-либо емкости и в окружающей атмосфере. Если давление емкости меньше атмосферного, его называют разряжением.

Вязкость. Если в потоке газа (жидкости) существует градиент скорости в направлении, перпендикулярном к направлению движения (ось х), то между слоями жидкости возникают касательные напряжения, величина которых определяется по закону Ньютона:

.

Рис. 2.

Коэффициент μ называют динамической вязкостью (не путать с химическим потенциалом). Т.к. напряжение измеряется в Па, т.е. Н/м², скорость в м/сек и расстояние в метрах, то размерность коэффициента μ должна быть: μ=[кг/м·сек]. Величина μ зависит от природы газа или жидкости и температуры: вязкость жидкостей уменьшается с температурой, а вязкость газов возрастает. Часто пользуются кинематической вязкостью, которая определяется как

Жидкость, в которой отсутствуют молекулярные связи, а, следовательно, и силы трения, называется идеальной жидкостью. Вязкость идеальной жидкости равна нулю. [Помнить! идеальным называется газ, подчиняющийся уравнению Клапейрона. Его вязкость не обязательно равна нулю.]

Расходом называется количество газа или жидкости, проходящее через некоторую площадь в единицу времени. В зависимости от того, в каких единицах измеряют количество газа или жидкости, расход может быть объемным или массовым (v или m). Согласно определению, v=dV/dτ и m=dM/dτ.

Между расходом, скоростью и сечением потока существует следующая связь:

v=wf (w – скорость, f – сечение) и m=ρwf.

Объемный и массовый расходы связаны между собой m=ρv.

При нагревании газа его объем увеличивается, следовательно, расход v возрастает. Между нормальным расходом (т.е. расходом при нормальных условиях) и расходом при температуре t существует связь:

v_T=v₀(1+βt).

Массовый расход не зависит от температуры газа.

Скорость в сечении потока обычно распределена неравномерно. В ряде расчетов скорость усредняют. Наиболее часто применяют среднюю расходную скорость, определяемую по выражению:

w=V/f.

Если в выражении v_t=v₀(1+βt) обе части разделить на f, получим соотношение w_t=w₀(1+βt).

Скорость звука есть скорость распространения малых возмущений. Связь между скоростью звука и сжимаемости среды, в которой он распространяется, выражается формулой

.

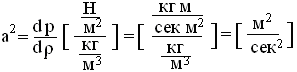Вследствие малой величины возмущений они распространяются практически без трения. Такой процесс можно считать изоэнтропным (т.е. идущим без изменения энтропии. Изоэнтропный процесс является одновременно и адиабатным, т.к. если dS=0 то и dq=0. При этом помнить, что адиабатный процесс не обязательно изоэнтропен).

Из уравнения Клайперона можно получить зависимость скорости звука от температуры:

a=√kRT

k – коэффициент теплопередачи.

Для этого необходимо сначала прологарифмировать, а затем продифференцировать уравнение адиабаты Пуансона p/ρ^k=const.

ln(p/ρ^k) = ln const = const; ln p – ln ρ^k = const; ln p – kln ρ = const;

dp/p - k'ln ρ –k(ln ρ)' = (const)'; dp/p – 0 – k(dρ∕ρ) = 0; dp/p = k(dρ/ρ);

dp/dρ = k(p/ρ) = a² , откуда p/ρ = a²/k .

Из закона Клапейрона , который может быть записан для удельного объёма газа как pv*= RT или, через плотность, p/ρ = RT, получаем следующее выражение, сделаем подстановку: a²/k = RT; отсюда а =√kRT.

Таким образом, для идеального газа скорость звука определяется его температурой.

Линия тока – это линия, касательные к которой в каждой точке совпадают с направлением скорости потока в этой точке. В установившемся потоке линии тока являются траекториями частиц. В потоке жидкости или газа можно выделить трубку, образующие которой дают линии тока. Движущаяся внутри трубки тока жидкость называется струйкой тока или просто струйкой. Струйку бесконечно малого сечения называют элементарной. Давление и скорость в поперечном сечении элементарной струйки постоянны.