Понятие сплошных сред. Теоретические основы механики сплошных сред

Процессы переноса энергии (тепла) и массы вещества являются одним из важнейших разделов современной науки и имеют большое практическое значение. Особое значение они имеют в реактивной и ракетной технике, где высота и скорость полета зависят от условий тепло – и массообмена.

Не меньшее значение процессы тепла и массообмена имеют в атомной энергетике при расчете и конструировании ядерных реакторов. При этом характерной особенностью переноса тепла и массы в указанных областях техники является их взаимосвязь, т.е. по сути дела они являются единым комплексным процессом.

Важно отметить, что законы, управляющие процессами тепло – и массообмена, одни и те же, а закономерности, полученные в одной области техники, могут с успехом применяться в другой. Это дает возможность коренным образом изменять процесс производства, создавать новые способы производства материалов и изделий. Научной основой теории тепло – и массопереноса являются гидравлика, термодинамика, молекулярная физика. Молекулярно-кинетическая теория явлений тепло – и массопереноса очень сложна, поэтому современная теория использует понятие сплошных сред, которое удобно применять не только к твердым телам, но также к газам и жидкостям. Это означает, что газ и жидкость рассматривают как сплошную подвижную среду, в которой отсутствует межмолекулярное пространство и межмолекулярное движение, а распределение вещества и физических свойств непрерывно.

Создание этих моделей привело к появлению такой науки, как механика сплошных сред.

Раздел механики сплошных сред, относящийся к газам и жидкостям, получил название «механика жидкости» или «гидромеханика». Однако развитие авиации привело к появлению аэромеханики – раздела, в котором изучается в основном взаимодействие воздуха с движущимися телами. Раздел механики сплошных сред, относящийся к движению газов с малыми скоростями (в промышленных печах) принято называть «механикой газов».

Раздел, посвященный движению газов с большими скоростями, называется «газовой динамикой».

Как уже говорилось, одной из базовых дисциплин в теории теплообмена является термодинамика (и массообмена тоже), поэтому нам придется вспомнить некоторые важные законы термодинамики, которые вы изучали ранее и, возможно, узнать новые.

Прежде всего, что это за наука? Возникла она как учение о тепловых машинах, но в дальнейшем сформировалась как самостоятельная фундаментальная дисциплина, которая изучает взаимные превращения тепла, работы и различных видов энергии. Как всякая наука, термодинамика оперирует целым рядом понятий и терминов. Важнейшим из них является понятие системы. Системой называется мысленно выделенная из среды совокупность материальных объектов. Система, в которой происходит массо – или теплообмен между составляющими ее объектами называется термодинамической. В зависимости от степени защищенности системы от окружающей среды они могут быть изолированными (совершенно не взаимодействующими с окружающей средой), закрытые (взаимодействуют с окружающей средой, не обмениваясь веществом, например, только путем теплообмена) и открытые (обмениваются с окружающей средой частицами, составляющими их вещество).

Состояние термодинамической системы характеризуется величинами, которые называют термодинамическими параметрами или просто параметрами.

Важнейшими термодинамическими параметрами системы являются температура, давление и объем. Эти параметры хороши тем, что они имеют достаточно ясный смысл и их сравнительно легко измерить. Параметры (термодинамические параметры) термодинамических систем связаны между собой. Соотношения, выражающие на языке математики эту связь, называют уравнениями состояния. С уравнениями состояния вы встречались еще в школе – вспомните законы Бойля – Мариотта, Гей-Люссака, а также объединенный газовый закон: где m – масса газа, M – молярная масса.

Однако p, V и T далеко не единственные параметры, используемые для характеристики состояния термодинамических систем.

Наряду с ними используются и другие:

1- Внутренняя энергия U. Для конденсированного тела (т.е. твердого или жидкого) включает кинетическую энергию движущихся молекул, потенциальную энергию их взаимодействия, а также энергию частиц, составляющих атом, в том числе и ядерную. Скорости молекул определяются температурой, а, следовательно, температурой определяется и кинетическая энергия. Потенциальная энергия определяется расстоянием молекул друг от друга. Поэтому внутренняя энергия зависит от T и V, т.е. U=f(T,V).В случае идеального газа энергия взаимодействия между его молекулами очень мала по сравнению с кинетической, собственный объем мал по сравнению с объемом газа. Поэтому внутренняя энергия идеального газа не зависит от объема. Ее можно вычислить по формуле dU=MCvdT. Поэтому расширение идеального газа в пустоту не сопровождается изменением температуры. Если термодинамическая система, например, сосуд с газом, не является изолированной системой, ему можно сообщить энергию извне. Эта энергия может расходоваться на производство работы (подъем поршня), а также на увеличение внутренней энергии системы (повышение температуры). Между количеством тепла, поступившим в систему, работой и изменением внутренней энергии существует связь: q=U+A или для бесконечно малых процессов dq=dU+dA. Это математическое выражение первого закона термодинамики. Количество тепла, полученного системой, равно увеличению ее внутренней энергии и произведенной ею работы. Этот закон есть приложение универсального закона сохранения энергии к процессам, происходящим с выделением или поглощением тепла. Он гласит: при всех взаимных превращениях энергии энергия не теряется и не создается. В изолированной системе сумма всех видов энергии постоянна.

В зависимости от характера процесса сопровождающее его изменения внутренней энергии может по-разному распределяться между теплом и работой. Например, при расширении газа в пустоту, работа равна нулю. Важное свойство внутренней энергии состоит в том, что ее изменение зависит только от энергии начального U₁ и конечного U_2, состояния и не зависит от пути процесса. Поэтому внутреннюю энергию называют функцией процесса. Следует отметить, что работа и теплота функциями процесса не являются. Вообще следует помнить, что теплота и работа характеризуют формы передачи энергии, а не саму энергию.

2- Энтальпия.

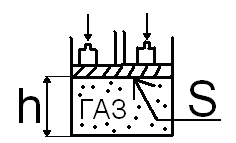
Рассмотрим систему: цилиндр с газом закрыт поршнем. Поршень нагружен внешней силой, создающей давление p.

S- площадь поршня,

h- высота подъема поршня,

U- внутренняя энергия газа в цилиндре.

Рис 1

Тогда энергия поршня: pSh=pV, а полная энергия системы: U+pV=H – энергия «расширенной системы», или энтальпия.

Изменение энтальпии при протекании термодинамического процесса определяет выражение: dH=dU+Ad(pV) или при переходе к удельным величинам: di=dU+ Ad(pv*). Символом i пользуются наряду с символом H, A- в данном случае тепловой эквивалент работы. Для подсчета изменения энтальпии при переходе системы из состояния 1 в состояние 2 проинтегрируем последнее выражение: i₂-i₁=U₂-U₁+A(p₁v₁*-p₂v₂*).

3- Энтропия.

При контакте двух тел с разной температурой, тепло всегда переходит от более нагретого тела к менее нагретому. Однако, с точки зрения первого закона термодинамики, возможен и противоположный процесс, т.е. повышение температуры нагретого тела за счет охлаждения менее нагретого, т.к. при этом соблюдается энергетический баланс (т.е. выполняется первый закон термодинамики). Видно, что для предсказания направления физических и химических процессов необходим другой принцип – второй закон термодинамики. Согласно этому закону, невозможно перевести тепло от более холодного тела к более нагретому при отсутствии других изменений в обоих телах или окружающей среде. Второй закон термодинамики отражает односторонность всех протекающих в природе процессов. Такие процессы называются естественными или необратимыми, и являются самопроизвольными. Они неуклонно приводят к конечному состоянию равновесия. Система в таком состоянии не может вернуться сама собой ни в одно из своих предыдущих состояний. Природа всегда «предпочитает» конечные состояния исходным. Второй закон термодинамики отражает универсальный характер этого явления. Его простейшая формулировка гласит, что переход тепла от холодного тела к более теплому не может происходить самопроизвольно. Для осуществления такого процесса нужно затратить работу.

Второй закон и необратимость естественных процессов является следствием атомно – молекулярной природы вещества и хаотичного характера теплового движения частиц. Очевидно, что все реальные процессы отличаются по степени необратимости. Для количественной оценки степени необратимости было введено понятие энтропии. Целесообразно это понятие связывать с количеством тепла, которое подводится к термодинамической системе и с температурой. Если обозначить через S_a энтропию в начале процесса, а через S_b в конце, то можно записать S_b-S_a=Q\T или короче S=Q\T.

Однако знак равенства в этом уравнении можно ставить, только если термодинамический процесс идет бесконечно медленно и не сопровождается потерями тепла. Такой процесс называют обратимым. В случае же протекания естественных (необратимых) процессов следует помнить, что изменение энтропии не зависит от характера процесса т.к. она является функцией состояния, а вот работа (тепло) всегда меньше, чем в случае обратимого процесса (они не являются функциями состояния). Поэтому для характеристики необратимых процессов мы должны написать: S>Q\T. Для бесконечно малых процессов dS>dq\T.

4- Свободная энергия.

Большинство металлургических процессов протекают не в замкнутых системах и сопровождаются теплообменом, поэтому энтропия уже не является критерием равновесия, необходимо выбрать другую функцию. Эту функцию можно построить на основе понятия работы, если рассмотреть частный случай, когда при постоянной температуре работу можно считать функцией состояния. Объединим для этого уравнения первого и второго начала термодинамики: dq=dU+dA и dS=dq\T (для обратимых процессов) и получим следующее уравнение: dA=TdS-dU. При условии постоянства температуры ее можно внести под знак дифференциала: dA=-d(U-TS). Таким образом, работа при изотермическом обратимом процессе равна убыли новой функции, определяемом тождеством F=U-TS или dA=-dF. Для обратимых процессов dA<-dF. Изменение F не зависит от пути процесса, т.е. она является функцией состояния и называется свободной энергией Гельмгольца. Если процесс протекает при постоянном объеме, отсутствует работа расширения: dA=pdV=0. Следовательно, dF≤0. Отсюда вытекает важный вывод: при необратимых процессах свободная энергия может только уменьшаться и лишь при протекании обратимых изотермических процессах при постоянном объеме она не меняется.

На практике чаще процессы протекают при постоянном давлении, при котором совершается работа dA=pdV. Поэтому получается неравенство: dF+pdV≤0. Если давление постоянно, то p можно внести под знак дифференциала и получить для необратимых процессов d(F+pV)<0, для обратимых d(F+pV)=0. Новая функция состояния определяется тождеством: G=F+pV и называется свободной энергией Гиббса (G=U-TS+pV или G=H-TS).

В системах при постоянных p и T самопроизвольно могут идти только процессы, сопровождающиеся уменьшением G, а условием равновесия является dG=0.

Доказательство:

К общим частям неравенств dA=<-dF прибавляем dF. Получим: dA+dF≤-dF+dF, отсюда pdV+dF≤0.

P.S. Все параметры, которые мы с вами вспомнили, являются термодинамическими параметрами состояния системы (помимо температуры, давления и объема).