Вопрос 17

Уравнения плоскости

Впервые встречается у А. К. Клеро (1731).

Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818).

Нормальное уравнение ввёл Л. О. Гессе (1861).

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

• Общее уравнение (полное) плоскости

где и  — постоянные, причём и одновременно не равны нулю; в векторной форме:

где  — радиус-вектор точки , вектор перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора :

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При плоскость проходит через начало координат, при (или , ) П. параллельна оси (соответственно или ). При ( , или ) плоскость параллельна плоскости (соответственно или ).

• Уравнение плоскости в отрезках:

где , ,  — отрезки, отсекаемые плоскостью на осях и .

• Уравнение плоскости, проходящей через точку 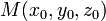перпендикулярно вектору нормали :

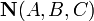в векторной форме:

• Уравнение плоскости, проходящей через три заданные точки 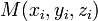, не лежащие на одной прямой:

(смешанное произведение векторов), иначе

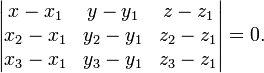
• Нормальное (нормированное) уравнение плоскости

в векторной форме:

где - единичный вектор,  — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

(знаки и противоположны).

Вопрос 18

Прямая в пространстве задается как линия пересечения двух плоскостей:

Если выбрать плоскости, проектирующие прямую на координатные плоскости, то получим канонические уравнения прямой:

где (а, b, с) - данная на прямой точка; l, m, n - проекции на оси координат какого-либо вектора, параллельного данной прямой; числа l, m, n пропорциональны направляющим косинусам прямой:

(знак перед корнями может быть взят любой, но одинаковый во всех трех равенствах; α, β, γ - углы между прямой и осями координат).

Угол φ между двумя прямыми отыскивается из равенства

Условие параллельности двух прямых: l₁/l₂ = m₁/m₂ = n₁/n₂. Условие перпендикулярности: l₁l₂+m₁m₂+n₁n₂=0.

Условие параллельности прямой и плоскости: Аl+Bm+Cn=0. Условие перпендикулярности прямой и плоскости: А/l = В/m = С/n

Прямая пересекает плоскость в одной точке. Точку пересечения прямой с плоскостью определяют путем построения вспомогательной прямой линии, лежащей в одной проецирующей плоскости с заданной прямой. На рис. 119, а приведен комплексный чертеж прямой l и плоскости 9 (ABC), причем т ~ Q (ABC). Через горизонтальную проекцию прямой l₁ проводим проекцию вспомогательной горизонтально проецирующей плоскости Sum₁. В пересечении плоскостей Q и Sum получаем линию т, то есть т =Sum ^ Q. Горизонтальная проекция прямой т определяется горизонтальными проекциями точек 1 и 2 пересечения линий ЕС и АС со вспомогательной плоскостью Sum , то есть В₁С₁ ^ Sum = l₁; А₁С₁ ^ Sum₁=2₁; т₁ = l₁^2₁.