
- •Тема 1. Экономическая сущность инвестиций.
- •Тема 2 Введение в теорию денежных потоков.
- •Тема 3. Понятие будущей стоимости.
- •Критерии эффективности инвестиционных проектов
- •Чистой текущей стоимости (чтс,npv)
- •Критерий индекса доходности
- •Критерий внутренней нормы доходности (внд)
- •Срок окупаемости инвестора
- •Оценка эффективности единственного проекта
- •Оценка эффективности нескольких проектов.
- •Тема Виды эффективности инвестиционных проектов
- •Народнохозяйственные результаты
- •Тема Оценка эффективности проектов, имеющих разную длительность
- •Продление проектов за счет использования первоначальных инвестиций
- •Продление срока жизни космических объектов
- •Метод наименьшего общего кратного (нок)
- •Метод определения постоянного денежного потока
- •Метод реинвестирования
- •Тема Оценка рисков инвестиционных проектов
- •Тема Оценка рисков инвестиционных проектов с использованием нормального закона распределения
- •Методы оценки рисков и их классификация
- •Оценка рисков на основе формирования сценариев
- •II. Метод аналогии
- •III. Метод сетевого планирования управления (спу)
- •Классификация рисков
- •Внутренние
- •Внешние на микроуровне
- •Внешние на макроуровне
- •Внутренние риски хозяйствующего субъекта
- •Применение спу при оценке эффективности инвестиционных проектов
- •Основные параметры сетевых моделей
- •События
- •Правила построения сетевых моделей
- •Типы сетевых моделей
- •Области применения спу
- •Вероятностные сетевые модели
- •Параметры двухоценочной системы
- •Особенности применения всм
- •Многоуровневая оценка эффективности инвестиционных проектов
- •Тема Многоуровневая оценка
- •Однокритериальные одноуровневые задачи
- •Тема Оценка эффективности инвестиционных проектов с учетом интересов различных участников и заинтересованных сторон.
- •Тема Проблемы оценки инвестиционных проектов
Тема Оценка рисков инвестиционных проектов
Вероятностный подход к оценке рисков
![]() ,
где
,
где
![]() - риск
- риск
![]() - вероятность
- вероятность
![]() – требуемый результат
– требуемый результат
![]() – фактический результат.
– фактический результат.
Под результатом понимаются те или иные оценки эффективности инвестиционных проектов.
![]() ,
где
,
где
![]() .
.
Основные вероятностные критерии оценки рисков
Рассмотрим дискретную постановку задачи:
Есть
![]() ,
,
![]() …
…![]() – показатели эффективности (ВНД, срок
окупаемости…).
– показатели эффективности (ВНД, срок
окупаемости…).
![]() – вероятности.
– вероятности.
Математическое ожидание:

Дисперсия:

Среднеквадратичное отклонение:
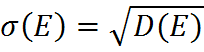
В качестве основного показателя, характеризующего риск, выступает среднеквадратичное отклонение, т.к. оно характеризует разброс около математического ожидания показателя эффективности.
При
этом возникает задача установления
связи между показателями эффективности
![]() и среднеквадратичного отклонения
и среднеквадратичного отклонения ![]()
Как правило, эта связь является противоречивой, т.е. с повышение показателя эффективности – увеличивается среднеквадратичное отклонение, т.е. риск.
Если мы хотим повысить эффективность, то надо помнить о вероятности увеличения риска.

На рисунке показана зависимость между показателями эффективности и риском.

![]() ,
, ![]()
Из рисунка видно, что Проект 1 имеет меньшую эффективность, но и меньший риск, а второй Проект наоборот – большую эффективность и больший риск.
В ситуациях, когда имеются противоречия между эффективностью и риском – возникает неопределенность выбора наиболее предпочтительного решения.
Правильный выбор будет зависеть от ряда факторов:
Финансового состояния фирмы
Имиджа компании
Особенности лиц, принимающих решения
Оценка риска при непрерывных вероятностных процессах
В отличие от дискретного распределения – при непрерывном распределении осуществляется переход от вероятности (P) к плотности вероятности (W).
При этом основные вероятностные характеристики записываются виде:
Математическое ожидание:

Дисперсия:

Среднеквадратичное отклонение:
![]()
В случае непрерывного распределения случайных величин, при определении риска, используют следующую характеристику:

При этом определяются величины:
P
(![]() )
)

В
данном случае ![]() будет характеризовать нижнюю границу
эффективности;
будет характеризовать нижнюю границу
эффективности; ![]() - верхнюю границу эффективности проекта.
- верхнюю границу эффективности проекта.
P
(![]() )
- эта вероятность показывает то, что
эффективность проекта будет находиться
в указанных пределах.
)
- эта вероятность показывает то, что
эффективность проекта будет находиться
в указанных пределах.
Наряду с указанной характеристикой, определяют следующую характеристику:

Тема Оценка рисков инвестиционных проектов с использованием нормального закона распределения
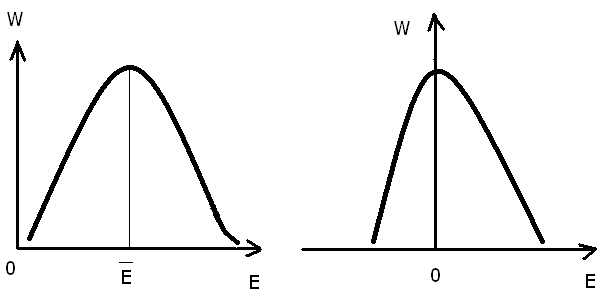
![]() - математическая запись закона
распределения.
- математическая запись закона
распределения.
 b
=
b
=
![]() - экономическая запись закона
распределения.
- экономическая запись закона
распределения.
При оценке рисков с помощью вероятностных законов распределения, особое значение имеет применение нормального закона распределения (закона Гауса).
Это обусловлено тем, что во многих случаях анализируемая величина эффективности зависит от множества независимых факторов.
В данных ситуациях, проводимые вычисления существенно упрощаются.
Свойство: Отдельные случайные величины перемножаются, чтобы найти нормальное распределение.
При применении нормального закона распределения будет справедливо следующее соотношение:

![]() и
и ![]() - табличные функции, которые приводятся
в математических справочниках, поэтому
располагая величинами, приведенными в
скобках 𝛽,
𝛼,
σ, E
– определяем вероятность того, что
величина эффективности будет находиться
в заданных пределах.
- табличные функции, которые приводятся
в математических справочниках, поэтому
располагая величинами, приведенными в
скобках 𝛽,
𝛼,
σ, E
– определяем вероятность того, что
величина эффективности будет находиться
в заданных пределах.
Применение графика безубыточности для оценки риска проектов

TR=P∙Q, где P -цена, Q – количество
TC=FC+VC’∙Q
TR=TC, тогда Прибыль=0
P∙Q= FC+VC’∙Q
P∙Q−VC’∙Q = FC
Q
=
При использовании графика безубыточности вводится понятие индекса безопасности, он определяется по формуле:

При
выборе ![]() необходимо устанавливать соотношение
между спросом и предложением: предложение
определяет производитель, спрос –
потребитель.
необходимо устанавливать соотношение
между спросом и предложением: предложение
определяет производитель, спрос –
потребитель.
