Тема 10. Описательный анализ. Базовые методы анализа маркетинговой информации

План:

10.1. Вариационный ряд: характеристика распределения данных.

10.2. Обобщающие показатели: интерпретация типических значений. Среднее. Медиана. Мода. Перцентили. Квартили. Блочная диаграмма.

10.3. Показатели вариации. Размах вариации. Межквартильный размах.

10.4. Стандартное отклонение. Коэффициент вариации.

10.5. Понятие «статистическая гипотеза».

10.1. Вариационный ряд: характеристика распределения данных

Вариационный ряд, распределение частот значений переменной - математическое распределение, цель которого - подсчет ответов, связанных с различными значениями одной переменной (частот), и дальнейшее выражение их в процентном виде (частости).

Вариационный ряд - упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины. Равные между собой элементы выборки нумеруются в произвольном порядке.

Целью построения вариационного ряда является подсчет ответов респондентов, в которых приводятся различные значения переменной. Относительную частоту различных значений переменной выражают в процентах и называют частостями. Подсчет распределения частот значений переменной дает возможность построить таблицу, с указанием частоты, частости и накопленных частостей для всех значений этой переменной.

Вариационный ряд помогает определить долю неответивших респондентов, а также указывает долю ошибочных ответов. Значения, равные 0 или 8, соответствуют ошибочным ответам. Следует определить количество случаев с такими значениями и соответственно откорректировать результат. Кроме того, можно установить наличие выбросов, т.е. случаев с экстремальными значениями. Распределение частот также определяет форму эмпирического распределения значений переменной. Частотные данные можно использовать для построения гистограмм или вертикальных столбчатых диаграмм, на которых по оси Х откладывают значения переменной, а по оси Y - абсолютные (частоты) или относительные (частости) значения.

Например, приведены оценки 45 студентов по дисциплине «Маркетинговые исследования» в порядке сдачи экзамена:

5 3 3 4 2 4 4 3 5 4 4 5 5 4 4

3 3 3 2 5 5 4 4 4 3 4 3 4 5 4

4 4 4 3 3 4 3 4 3 2 3 2 3 3 3

При таком представлении информации трудно делать какие-либо выводы об успеваемости. Поэтому необходимо произвести группировку данных путем подсчета количества различных оценок:

оценки 2 3 4 5

количество 4 6 18 7

Как видно, вместо 45 чисел осталось 8, при этом повысилась информативность, более 50% студентов сдали предмет на хорошо и отлично.

Данный пример показывает, что эти данные лучше сгруппировать, то есть разделить их на однородные группы по некоторому признаку. Благодаря группировке данные приобретают систематизированный вид. Если данные систематизированы по времени, то моделью группировки будет временный ряд. Если же по любому другому признаку - то ряд распределения, а для количественных признаков - вариационный ряд.

10.2. Обобщающие показатели: интерпретация типических значений. Среднее. Медиана. Мода. Перцентили. Квартили. Блочная диаграмма

Обобщающими показателями, применяемыми для интерпретации типичных значений, являются следующие:

• среднее арифметическое (X);

• медиана (Ме);

• мода (Мо);

• перцентили;

• квартили.

Эти показатели используются при ответе на вопрос «каково типичное значение признака для данного распределения?».

Среднее арифметическое представляет собой сумму всех значений признака, делённую на объём выборки (10.1):

(10.1)

где X_i - значения признака;

n - объём выборки.

Если значения признака повторяются и представлены в виде вариационного ряда, то формула для вычисления среднего арифметического принимает вид (10.2):

или (10.2)

где f_i - абсолютная частота распределения,

f_i (%) - относительная частота,

n - объём выборки.

Медиана - это 50-й процентиль в группе данных, значение признака, которое делит упорядоченное множество данных пополам, так, что число объектов с большим и меньшим, чем медиана, значением признака одинаково.

Медиана определяется для количественных, а также для качественных признаков, измеренных с помощью порядковых шкал. Медиана может быть определена:

приблизительно по распределению накопленных частот;

по графику накопленных частот;

по формуле внутри медианного интервала.

Медианный интервал - это такой интервал, для которого накопленная частота является самой маленькой из всех накопленных частот, превышающих 50% объёма выборки.

Например, при оценках, полученных от экспертов, - 7, 6, 9, 8, 7; упорядоченный ряд будет выглядеть как 6, 7, 7, 8, 9. В этом случае медианой будет значение «7», так как оно стоит в центре упорядоченного ряда.

Мода представляет собой типическое среднее, т.е. значение признака, наиболее характерное для данной выборочной совокупности.

Модой называется значение признака, обладающее наибольшей частотой. Мода определяется для качественных и количественных признаков, измеренных с помощью любых типов шкал. Для номинальных и порядковых типов шкал мода определяется по частотному распределению. Значения признака, обладающие наибольшей частотой, являются модальными значениями.

Для количественных признаков, сгруппированных в интервалы, модальным является интервал, соответствующий наибольшей частоте (если интервалы одинаковые) или соответствующий наибольшей плотности (если интервалы разной длины).

Например, при оценках, полученных от экспертов, - 7, 6, 9, 8, 7; в этом случае модой будет наиболее популярное и часто встречающееся значение. Это «7».

Перцентиль - одна из числовых характеристик распределения вероятностей; частный случай квантили.

Квартиль в математической статистике - значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Квартиль часто используются при анализе продаж, чтобы разбить генеральную совокупность на группы.

Указывает на место расположения данных выборки или распределения. Когда значение находится в зоне, где расположено менее 25% наблюдаемых значений переменной, то говорят, что оно расположено в нижнем квартиле. Если же оно расположено там, где находятся верхние 25% значений, то говорят, что оно расположено в верхнем квартиле.

Блочная диаграмма - один из видов графического изображения статистических распределений какой-либо величины по количественному признаку. Представляет собой совокупность смежных прямоугольников, построенных на одной прямой; площадь каждого из них пропорциональна частоте нахождения данной величины в интервале, на котором построен данный прямоугольник.

Блочная диаграмма содержит один или несколько блоков, которые представляют распределение данных в одном или нескольких наборах данных. На блочной диаграмме выводится вертикальный прямоугольник, с обеих сторон которого расположены линии ограничителя выбросов (рис.10.1).

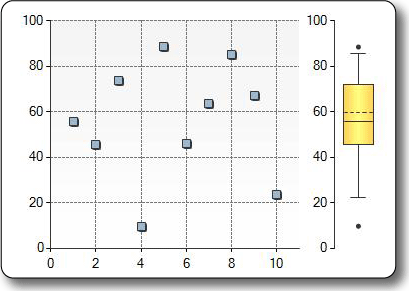
Рис.10.1. Пример изображения блочной диаграммы

Значения для блока обычно вычисляются из данных, которые присутствуют в других рядах. Один символ блока сопоставляется с одним рядом данных. При этом данные для блочной диаграммы можно заполнять с помощью привязки данных.