Свойства

1. Линейность:  ;

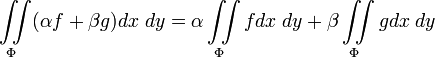2. Аддитивность:  ;

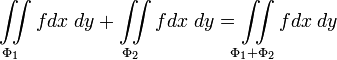3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.

38. Формула Гаусса-Остроградского и её приложения к вычислению поверхностных интегралов и объемов пространственной области.

Тройной интеграл после вычисления первого внутреннего интеграла превращается в двойной интеграл, который можно выразить через поверхностный.

Имеем тело ограниченное гладкими поверхностями : G1 – низ ,

 z = z0(x,y) ; G2 – верх, z = Z(x,y) ; G3 - цилиндрическая боковая поверхность по границе области  D на плоскости хОу. В этом объеме V определена функция R(x,y,z) , причем, функция и ее производные непрерывны. Рассмотрим интеграл

J=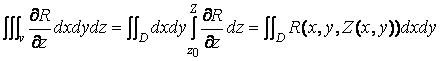 - - = J1 – J2

 По формуле ( 13 ) интеграл J1 сводится к интегралу по внешней поверхности «верха» тела, а J2 по внутренней поверхности «низа». При переходе на внешнюю сторону «низа» знак J2 меняется. Учтем также, что аналогичный интеграл J3 по боковой поверхности G3 равен нулю, т.к. площадь ее проекции на плоскость хОу равна нулю. В итоге имеем

J =   +   + 

где интегралы вычисляются по внешней стороне поверхности ограничивающей тело, или

 ( 18 )

Обобщение формулы ( 18 ) на случай тела произвольной формы приводит к формуле Остроградского – Гаусса

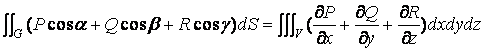 ( 19 )

которая интеграл по объему заменяет на интеграл по внешней стороне поверхности ограничивающей тело.

Вычисление объема.

Пусть подынтегральная функция в ( 4 ) не зависит от z , тогда она определяет некоторую поверхность z = f(x,y) , а интеграл по D объем цилиндрического бруса, ограниченного этой поверхностью и областью D . Переход к поверхностному интегралу в этом случае дает следующее выражение для объема цилиндрического бруса V =   ( 14 ) Понятие о комплексных числах. Определение. Комплексным числом z называется выражение  , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:   При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).

Обобщение этой формулы на случай тела произвольной формы ограниченного поверхностью G имеет вид V = 1/3   ( 15 )

36. Поверхностный интеграл 1-го рода, Его свойства. Вычислительная форма

     Сведение к двойному 

     1. Поверхность S задана уравнением 

где   - величина угла между нормалью к поверхности и положительным направлением оси Oz.

     2. Поверхность S задана параметрически: 

где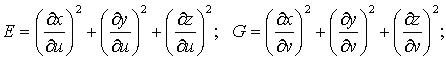 

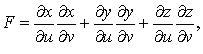 или

где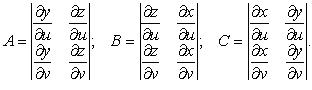 

Свойства

1. Линейность:  ;

2. Аддитивность:  ;

3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.

33. Явные представления поверхности

32. Касательная плоскость и нормаль к поверхности

Пусть поверхность   задана уравнением                                     (1)

в неявном виде. Будем считать, что   и в некоторой окрестности точки   функция   имеет непрерывные частные производные, одновременно не равные нулю. Тогда

                 (2)

Мы пишем   вместо  .

Для определенности предположим, что  . Тогда на основании теоремы о неявной функции  существует окрестность точки  , в которой поверхность   описывается явно непрерывно дифференцируемой функцией  . Уравнение касательной плоскости к   в точке  , как мы знаем, имеет вид

,

где

.

В силу этого уравнения касательной плоскости к   в точке   запишется так:

,                (3)

а уравнение нормали к   в точке   - так:

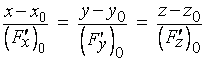.                                   (4)

Те же уравнения (3), (4) мы получим, если предположить, что   или  . В этих случаях в окрестности   поверхность   описывается явно соответственно уравнениями

.

Мы видим, что при условии (2) поверхность   в любой точке   имеет касательную плоскость, непрерывно изменяющуюся при непрерывном передвижении точки  . Такую поверхность называют гладкой поверхностью  .

Другое дело, если  . В этом случае нельзя гарантировать, что в точке   существует касательная плоскость к  . Она может существовать, а может и не существовать.

 31. Ориентация гладкой поверхности

Гладкая поверхность ориентируема, если можно построить на ней непрерывное поле единичных нормальных векторов. Это поле единичных нормалей определяет ориентацию (или сторону) поверхности. На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов:

Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), как и неориентируемыми (односторонними).

30. Параметрически заданные поверхности. Криволинейные координаты на поверхности

29. Эквивалентные элементарные поверхности

28. Пример шварца. Площадь поверхности

если поверхность задана параметрически кусочно  -гладкой функцией  , где параметры  ,   изменяются в области   на плоскости  , то площадь   выражается двойным интегралом

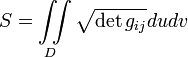
где  ,  ,  , a   и   — частные производные по   и  . В частности, если поверхность есть график  -гладкой функции   над областью   на плоскости  , то

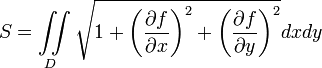
На основе этих формул выводятся известные формулы для площади сферы и её частей, обосновываются приёмы для вычисления площади поверхностей вращенияи т. п.

27. Понятие поверхности. Виды поверхностей. Элементарные поверхности

26. Независимость криволинейного интеграла второго рода от пути интегрирования. Признак Грина

Пусть D - некоторая замкнутая область на плоскости хОу, ограниченная контуром L. На ней заданы функции Р = Р(х,у) и Q = Q(x,y), непрерывные на D вместе со своими частными производными первого порядка. Формула Грина связывает криволинейный интеграл второго рода по L с двойным интегралом по области D:

Движение по контуру L - в положительном направлении.

С помощью формулы Грина значение криволинейного интеграла по замкнутому контуру можно найти, вычислив двойной интеграл.

 20. Формула Грина для многосвязной области

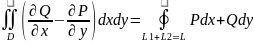
Формулу Грина можно применять, если область D – замкнутая, ограниченная кусочно-гладким контуром L, функции P(x,y) и Q(x,y) непрерывны и имеют частные производные первого порядка: 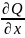и .

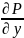19. Формула Грина для односвязной области

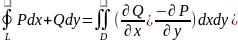
Формулу Грина можно применять, если область D – замкнутая, ограниченная кусочно-гладким контуром L, функции P(x,y) и Q(x,y) непрерывны и имеют частные производные первого порядка: и .

15. Криволинейный интеграл 1-го рода и его свойства. Вычислительная формула

Определение: Если при ∆l→0, σ имеет конечный предел, не зависящий ни от способа разбиений, ни от выбора точек Mk, то этот предел называется криволинейным интегралом первого рода от функции f(M) по кривой AB (интегрируется по длине дуги кривой) и обозначается 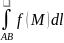или . Таким образом .

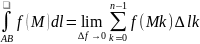Свойства: 1) Криволинейный интеграл первого рода не зависит от направления интегрирования; 2) Линейность; 3) Аддитивность; 4) Если f(M)≥0, то 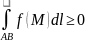; 5) f(M) интегрируема на АВ, следовательно |f(M)| тоже интегрируем на кривой АВ; 6) Среднее значение: 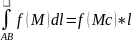, где l – длина кривой.

Способы вычисления криволинейного интеграла: 1) Кривая АВ: 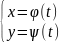, t0≤t≤t1, A→t=t0, B→t=t0, , ; 2)АВ: y=y(x), a≤x≤b, A→x=a, B→x=b, ,

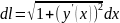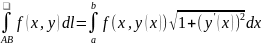
14. Физические приложении тройного интеграла

Масса и статические моменты тела

Пусть тело занимает объем U и его объемная плотность в точке M(x,y,z) задана функцией ρ(x,y,z). Тогда масса тела m вычисляется с помощью тройного интеграла:

Статические моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz выражаются формулами

Координаты центра тяжести тела вычисляются по формулам:

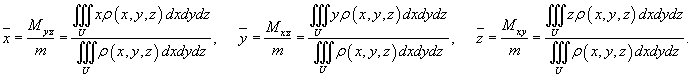
Если тело является однородным с плотностью ρ(x,y,z) = 1 для точек M(x,y,z) в области U, то центр тяжести тела зависит только от геометрии тела и называется центроидом. 

Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются выражениями

Тензор инерции

Используя рассмотренные выше 6 чисел I_x, I_y, I_z, I_xy, I_xz, I_yz, можно составить так называемую матрицу инерции или тензор инерции тела:

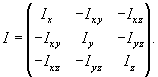
Гравитационный потенциал и сила тяготения

Ньютоновым потенциалом тела в точке P(x,y,z) называется интеграл

где ρ(ξ,η,ζ) − плотность тела, и  .  13. Вычисление объема тел с помощью тройного интеграла

Объем тела U в декартовых координатах Oxyz выражается формулой

В цилиндрических координатах объем тела равен

В сферических координатах, соответственно, используется формула

12. Замена переменных в тройном интеграле. Криволинейные координаты в пространстве. Сферическая система координат.

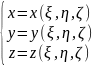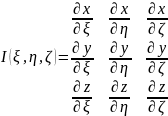Теорема о замене переменных в тройном интеграле: f(x,y,z) – непрерывна в замкнутой области Ω. – (1) непрерывны вмести со своими частными производными первого порядка в Ω*. - якобиан (функциональный определитель) системы функций (1).

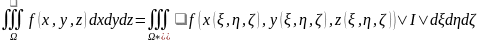
Вычисление тройного интеграла в сферических координатах: , , 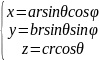|I|=abcr²sinθ, a=b=c=1 → сферические координаты

11. Замена переменных в тройном интеграле. Криволинейные координаты в пространстве. Целиндрическая система координат.

Теорема о замене переменных в тройном интеграле: f(x,y,z) – непрерывна в замкнутой области Ω. – (1) непрерывны вмести со своими частными производными первого порядка в Ω*. - якобиан (функциональный определитель) системы функций (1).

Вычисление тройного интеграла в цилиндрических координатах:

,

Якобиан перехода от декартовых координат к цилиндрическим равен

Тогда формула замены переменных при данном преобразовании имеет вид:

Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью. 

10. Перестановка порядка интегрирования в тройном повторном интеграле

9. Свойства тройного интеграла

Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства:

1. 

2. 

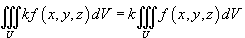3. , где k - константа;

4. Если 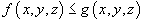  в любой точке области U, то  ;

5. Если область U является объединением двух непересекающихся областей U₁ и U₂, то ;

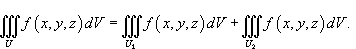6. Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x,y,z) в области U. Тогда для тройного интеграла справедлива оценка:

где V - объем области интегрирования U.

7. Теорема о среднем значении тройного интеграла. Если функция f (x,y,z) непрерывна в области U, то существует точка M₀ 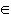  U, такая, что

где V - объем области U.