Дивергенция

— след такого тензора производных. Она не зависит от системы координат (является инвариантом преобразований координат, скаляром), а в прямоугольных декартовых координатах вычисляется по формуле:

Это же выражение можно записать с использованием символического оператора набла

Теорема Остроградского-Гаусса позволяет вычислить поток векторного поля с помощью объёмного интеграла от дивергенции поля.

[Править]Ротор

— векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:

,

где i, j и k — единичные орты для осей x, y и z соответственно.

Для удобства запоминания можно условно представлять ротор как векторное произведение:

[Править]Градиент

— важнейшая и простейшая операция, позволяющая получить векторное поле из скалярного поля. Полученное применением такой операции к скалярному полю fвекторное поле называется градиентом f:

или, записывая с помощью наблы:

Векторное поле, дивергенция которого всюду равна нулю, называется соленоидальным; оно может быть представлено как ротор некоторого другого векторного поля.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым); оно может быть представлено как градиент некоторого скалярного поля (потенциала).

Имеет место теорема Гельмгольца: если всюду в области D у векторного поля определены дивергенция и ротор, то это поле может быть представлено в виде суммы потенциального и соленоидального поля.

Векторное поле, у которого и дивергенция, и ротор всюду равны нулю, называется гармоническим; его потенциал представляет собой гармоническую функцию.

42. Векторное поле и способы его изучении с помощью векторных линий

  Определение 

     Векторное поле определяется векторной функцией точки

где   - точка пространства,   - ее радиус-вектор.

     Векторная линия 

     Векторная линия (силовая линия, линия тока) поля - решение системы

40. Формула Стокса её приложение к вычислению поверхностных интегралов

Известно, что формула Грина сводит двойной интеграл по плоской области D к криволинейному интегралу по контуру L , ограничивающему область D

 ( 16 )

Эта формула легко обобщается на случай, когда вместо куска плоской поверхности D берется кусок произвольной гладкой двухсторонней поверхности G , ограниченной контуром L. Формула Стокса :

   ( 17 )

переходит в формулу Грина, если положить  z = 0 . Тогда dz = 0 и G    D.

Из формулы Стокса легко получить условия при которых криволинейный интеграл по замкнутому контуру в пространстве обращается в ноль

 ;   ; 

39. Поверхностный интеграл 2-го рода, Его свойства. Вычислительная форма

по фиксированной стороне двусторонней поверхности S.

     Пови-2 по разным сторонам S⁺ и S ^- одной и той же поверхности S 

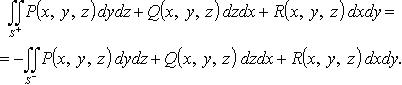
Сведение Пови-2 к двойному интегралу 

     1. Поверхность S задана параметрически: 

выбор знака перед интегралом согласуют со стороной поверхности, по которой ведется интегрирование.

     2. Поверхность S задана уравнением 

если Пови-2 вычисляется по верхней стороне поверхности S;

для нижней стороны поверхности S.