64. Свертка и преобразование Фурье

Свёртка фу́нкций — операция, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. В математике, свёртка — это математическая операция двух функций f и g, порождающая третью функцию, которая обычно может рассматриваться как модифицированная версия одной из первоначальных. По существу, это особый вид интегрального преобразования. Результат свёртки показывает в каких местах один сигнал похож на другой, а в каких непохож.

Пусть   — две функции, интегрируемые относительно меры Лебега на пространстве  . Тогда их свёрткой называется функция  , определенная формулой

В частности, при   формула принимает вид:

Свёртка   определена при почти всех   и интегрируема.

Свойства

• Коммутативность: .

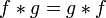• Ассоциативность: .

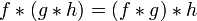• Линейность (дистрибутивность и умножение на число):

.

• Правило дифференцирования: ,

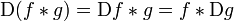где   обозначает производную функции   по любой переменной.

• Свойство Фурье-образа: ,

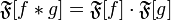где   обозначает преобразование Фурье функции  .

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции   вещественной переменной является интегральным и задаётся следующей формулой:

Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

61. Интегралы Лапласа

60. преобразование Фурье

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции   вещественной переменной является интегральным и задаётся следующей формулой:

Свойства

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса  , преобразование Фурье может быть определено и для более широкого класса функций и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

• Преобразование Фурье является линейным оператором:

• Справедливо равенство Парсеваля: если 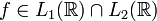 , то преобразование Фурье сохраняет 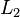 -норму:

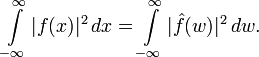
Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство  . Равенство Парсеваля будет при этом справедливо для всех  .

• Формула обращения:

справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция   является достаточно гладкой. Если  , то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний   с частотами  , амплитудами   и фазовыми сдвигами   соответственно.

• Теорема о свёртке: если 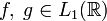 , тогда

, где

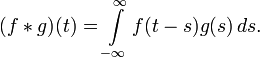
Эта формула может быть распространена и на случай обобщённых функций.

• Преобразование Фурье и дифференцирование. Если  , то

Из этой формулы легко выводится формула для  -й производной:

Формулы верны и в случае обобщённых функций.

• Преобразование Фурье и сдвиг.

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией  , а дифференцирование — свёртка с производной дельта-функции.

• Преобразование Фурье и растяжение.

• Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство  . Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции   её преобразованием Фурье называется обобщённая функция  , действующая на основные функции по правилу

Например, вычислим преобразование Фурье дельта-функции:

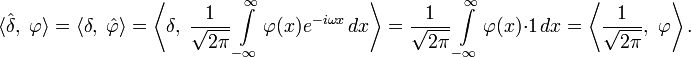
Таким образом, преобразованием Фурье дельта-функции является константа  .

58. Представление функции в виде интеграла фурье

Формула

имеет место, если

И в некотором интервале, содержащем точку x внутри, функция f(t) имеет ограниченное изменение или удовлетворяет какому-либо другому условию сходимости ряда или интеграла Фурье.

Д о к а з а т е л ь с т в о. достаточно доказать существование столь большого T, что

для всех значений λ > λ0. Очевидно, это имеет место при выполненииусловия I. Далее, убедимся в справедливости.

Остается доказать достаточность условия. Положим Тогда и требуемый результат следует из того, что xϕ(x) удовлетворяет условию.

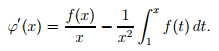
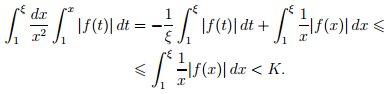
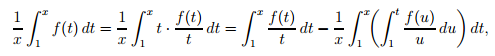
и так как f(t)/t, по условию I, принадлежит к L(1,∞), то правая часть этого равенства стремится к нулю.

57. В-функция и её своиства

бета-функцией ( -функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующаяспециальная функция от двух переменных:

,

определённая при  ,  .

Бета-функция была изучена Эйлером и Лежандром ^{[когда?]}, а название ей дал Жак Бине.

Свойства

Бета-функция симметрична относительно перестановки переменных, то есть

.

Бета-функцию можно выразить через другие функции:

,

где   — Гамма-функция;

;

;

,

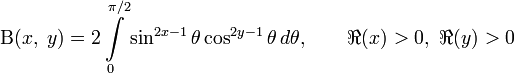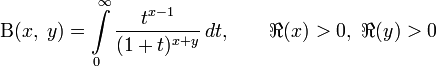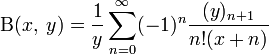где   — нисходящий факториал, равный  .

Подобно тому как гамма-функция для целых чисел является обобщением факториала, бета-функция является обобщением биномиальных коэффициентов с немного изменёнными параметрами:

.

55. График Г-функции и её аналитическое продолжение

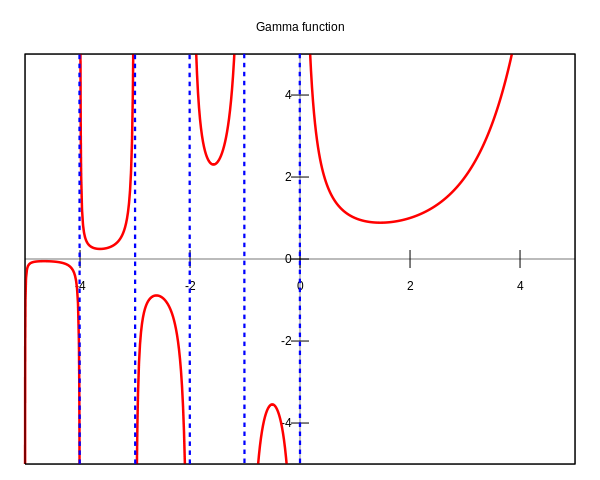
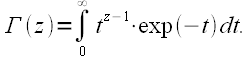
При этом для любых комплексных значений   справедливо равенство:

Данное рекуррентное соотношение является очень важным и используется при расчете гамма-функции. Приведем также формулу дополнения:

Можно заметить, что при отрицательных значениях  ,  , при этом гамма-функция для отрицательного аргумента может быть вычислена по формуле:

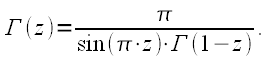
Необходимо отметить, что при целых  ,   и гамма-функция претерпевает разрыв.

54. Гамма функция и её свойства

 

Г(p)=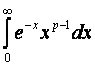

Непрерывность

Г-функция

сходящийся (по признаку Вейерштрасса)

=> равномерная сходимость по параметру, => подынтегральная функция непрерывна, => интеграл сходится к непрерывной функции,

=> Г-функция непрерывна

 

Дифференцируемость Г- функций

 

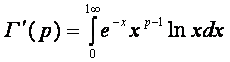
Г-функция бесконечное число раз дифференцируема, производные могут быть найдены внесением дифференцирования под знак интеграла.

 

Формулы понижения степени

 

Если n – натуральное число, то

53. Интегрирование несобственных интегралов, зависящих от параметров.

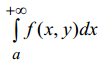(7)

и

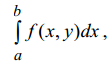(а − особая точка) (8)

называются сходящимися равномерно по переменной у, принадлежащей неко-

торой области U, если они сходятся при любом фиксированном значении y ∈U

и величина δ в критерии сходимости несобственного интеграла (см. п. 3.3) не

зависит от значения у, т.е.

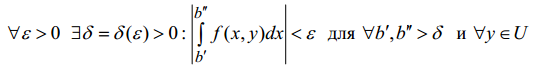− для интеграла (7),

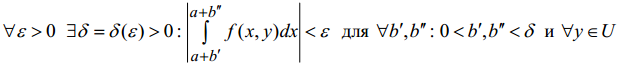− для интеграла (8).

Сформулируем свойства равномерно сходящегося интеграла (7). (Ана-

логичные свойства справедливы и для интеграла (8)):

Если функция f(х, у) непрерывна при х ≥ а и c ≤ у ≤ d и интеграл (7)

сходится равномерно при c ≤ у ≤ d, то функция

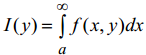непрерывна по у при c ≤ у ≤ d.

При условиях, сформулированных в свойстве 1, справедлива формула

интегрирования под знаком интеграла:

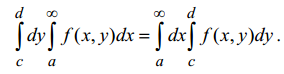
52. Дифференцирование несобственных интегралов, зависящих от параметров. 

(7)

и

(а − особая точка) (8)

называются сходящимися равномерно по переменной у, принадлежащей неко-

торой области U, если они сходятся при любом фиксированном значении y ∈U

и величина δ в критерии сходимости несобственного интеграла (см. п. 3.3) не

зависит от значения у, т.е.

− для интеграла (7),

− для интеграла (8).

Сформулируем свойства равномерно сходящегося интеграла (7). (Ана-

логичные свойства справедливы и для интеграла (8)):

Если функция f(х, у) непрерывна при х ≥ а и c ≤ у ≤ d и интеграл (7)

сходится равномерно при c ≤ у ≤ d, то функция

непрерывна по у при c ≤ у ≤ d.

Если функции f(x,y) и y f ′ (x,y) непрерывны, несобственный интеграл(7) сходится, а интеграл 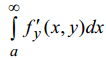сходится равномерно, то имеет место формула дифференцирования под знаком интеграла:

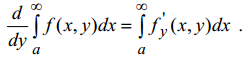
51. предельный переход по параметру, непрерывность несобственных интегралов, зависящих от параметров

) Если функция f(x, у )для почти всех  непрерывна по ув области  и если существует интегрируемая в Rⁿфункция g(x)такая, что для каждого   и для почти всех   справедливо неравенство   то интеграл J(y)является непрерывной функцией ув области G.

2) Если функция f(x, t), определенная при     для почти всех   и каждого   имеет производную  к-рая для почти каждого   является непрерывной функцией tна интервале (а, 6), и если существует интегрируемая в Rⁿ функция g(x)такая, что для каждого  и для почти всех   справедливо неравенство   то из существования при нек-ром   интеграла

1. Предельный переход под знаком интеграла.

Пусть для функции f (x,  ) при  существует конечная предельная функция   (х), т.е.

, (х из Х)

и f (x,  ) – интегрируемая и стремится к  (х) равномерно относительно х в конечном промежутке [a, A] при любом А>a. Если, сверх того, интеграл

сходится равномерно относительно   (в области  ), то имеет место следующая формула:

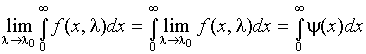. (84)

50. несобственные интегралы, зависящих от параметров, их равномерная сходимость.

Достаточный признак равномерной сходимости несобственного интеграла, зависящего от параметра

Пусть функция f (x,  ) интегрируема по х в конечном промежутке [a, A] (A   a).

Если существует такая, зависящая только от х функция  (х), интегрируемая в бесконечном промежутке  , что при всех значениях   в 

 

то интеграл (79) сходится равномерно относительно   (в указанной области его значений).

В этих условиях иногда говорят, что f (x,  ) имеет интегрируемую мажоранту  (х) или что интеграл 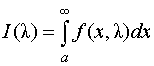мажорируется сходящимся интегралом  .

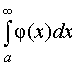49. Дифференцирование по параметру собственного интеграла с переменными пределами интегрирования

Теорема 2.9 Если функция f непрерывна и имеет непрерывную частную производную   на прямоугольнике П, то функция I(у) дифференцируема на отрезке [с; d] и справедливо равенство

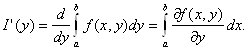 (2.3)

Доказательство. Так как   непрерывна на П, то, используя предыдущую теорему, для любого у   [с; d] можем написать равенство

 (2.4)

Упростим левую часть равенства 2.4 с помощью формулы Ньютона-Лейбница.

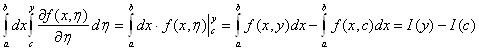
Обозначим через J(η) внутренний интеграл в правой части равенства (2.4). Тогда равенство (2.4) примет вид:

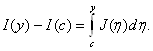 (2.5)

По теореме 2.7 J(η) — непрерывная на [с; d] функция. Но тогда по теореме о производной интеграла с переменным верхним пределом правая часть равенства (3.5) (следовательно, и левая) дифференцируема на отрезке [с; d]. По той же теореме из равенства (3.5) получаем:

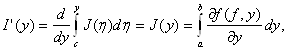
что и требовалось. ■ Рассмотрим теперь более общий случай, когда не только подынтегральная функция, но и пределы интегрирования зависят от параметра. Итак, пусть функция f(x, у) определена на прямоугольнике П =[а; Ь] х [с; d], интегрируема по х на отрезке [а; b] для каждого у   [с; d], функции а (у) и b(у) заданы на отрезке [с; d] и   [с; d] выполняется а ≤ а(у) ≤ b(у) ≤ b. Рассмотрим интеграл

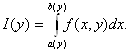 (2.6)

48. Дифференцирование по параметру собственного интеграла с постоянными пределами интегрирования

Теорема 2.10 Пусть функция f(x, у) непрерывна на П, а функции а(у), b(у) непрерывны на [с; d]. Тогда функция I(у), определённая равенством (2.6),непрерывна на [с; d].

Доказательство. Пусть y   [с; d]. Покажем, что  Для этого разобьём интеграл на три слагаемых, используя свойство аддитивности интеграла.

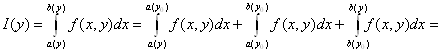
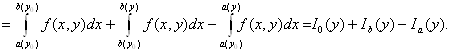 (2.7)

Здесь интегралы обозначены в порядке следования. Рассмотрим каждый из них в отдельности. Первый из интегралов — интеграл с постоянными пределами вида 2.1, его непрерывность доказана в теореме 2.7. Поэтому   

Займемся вторым интегралом. Функция f(x, у) непрерывна на П, следовательно, ограничена. Поэтому существует постоянная М такая, что

П.

Но тогда

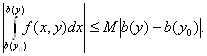
А так как функция b(у) непрерывна на [с; d], то   при  , поэтому   

Совершенно аналогично доказывается, что и 

Таким образом,

что и требовалось доказать.

47. Собственные интегралы, зависящие от параметра для прямоугольника и их свойства

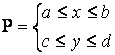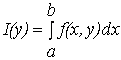Теорема 4 (о непрерывности интеграла как функции параметра). Пусть функция   определена и непрерывна в прямоугольнике  , тогда интеграл   будет непрерывной функцией от параметра   в промежутке  . Доказательство. Так как   непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике  . Возьмем любое   и зафиксируем  . Тогда нашему значению   будет соответствовать  , такое, что для любых двух точек  ,  принадлежащих  , из неравенств   и  , будет следовать  . Положим  ,  , где  ,  - любые из  , и  , где  . Тогда получим  . Это означает, что функция   равномерно стремится к  . В таком случае по теореме 3 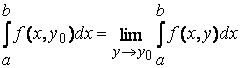 , а уже отсюда следует равенство  , то есть наша функция  непрерывна на  . Замечание 4. Совершенно аналогично доказывается теорема для 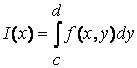 , где  . Следствие 2. Если   непрерывна на прямоугольнике  , то  .

45. Циркуляция векторного поля. Циркуляция как работа в силовом поле

Циркуля́цией ве́кторного по́ля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определению

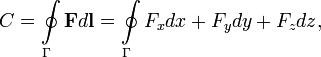
где   — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ,   — бесконечно малое приращение радиус-вектора   вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.

Свойства

Аддитивность

Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть

Формула Стокса

Циркуляция вектора F по произвольному контуру Г равна потоку вектора   через произвольную поверхность S, ограниченную данным контуром.

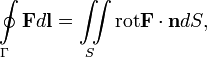
где 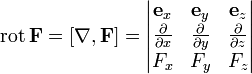  — ротор (вихрь) вектора F.

В случае, если контур плоский, например лежит в плоскости OXY, справедлива теорема Грина

где   — плоскость, ограничиваемая контуром   (внутренность контура).

Если F — некоторое силовое поле, тогда циркуляция этого поля по некоторому произвольному контуру Γ есть работа этого поля при перемещении точки вдоль контура Г. Отсюда непосредственно следует критерий потенциальности поля: поле является потенциальным когда циркуляция его по произвольному замкнутому контуру есть нуль. Или же, как следует из формулы Стокса, в любой точке области D ротор этого поля есть нуль.

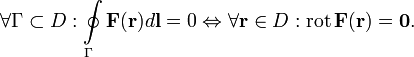
44. Поток векторного поля и его вычисление

Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.

Пусть поверхность S расположена в поле   скоростей частиц несжимаемой жидкости с плотностью ρ = 1. Можно показать, что поток векторного поля в этом случае равен

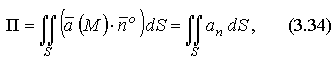
где   – единичный нормальный вектор к поверхности S, расположенный по одну сторону с вектором  , а величина  .

Независимо от физического смысла вектора   интеграл (3.34) по поверхности называют потоком векторного поля через поверхность S.

Пусть  и  тогда поток П вектора   через поверхность S можно записать в виде:

Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах:

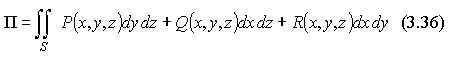
ПРИМЕР 1.  Ориентированные поверхности.

 

Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции  , где   - компоненты векторного поля,   - направляющие косинусы вектора нормали.

43. Основные операции теории поля: градиент, дивергенция, ротор