
- •Тема № 22. Функция комплексного переменного Определение функции комплексного переменного
- •Основные элементарные функции комплексного переменного
- •Тригонометрические функции
- •Логарифмическая функция – функция, обратная показательной.
- •Понятие многозначной функции
- •Комплексные числовые ряды.
- •[Править]Формула Тейлора
- •Ряд Лорана
- •СвойстваПравить
- •ПрименениеПравить
- •Особые точки и их классификация
- •Вычет фкп и его вычисление
Комплексные числовые ряды.






Ряд Тейлора
Определение
Пусть
функция ![]() бесконечно
дифференцируема в некоторой окрестности точки
бесконечно
дифференцируема в некоторой окрестности точки ![]() .
Формальный ряд
.
Формальный ряд
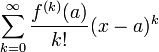
называется
рядом Тейлора функции ![]() в
точке
в
точке ![]() .
.
[править]Связанные определения
В случае, если
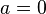 ,
этот ряд также называется рядом Макло́рена.
,
этот ряд также называется рядом Макло́рена.
[править]Свойства
Если есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке области определения сходится к в некоторой окрестности .
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности . Например, Кошипредложил такой пример:
![]()
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке равны нулю.
[Править]Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
-
Пусть функция имеет
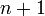 производную в
некоторой окрестности
точки
,
производную в
некоторой окрестности
точки
, 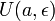
Пусть
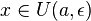
Пусть
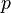 —
произвольное положительное число,
—
произвольное положительное число,
тогда:
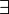 точка
точка 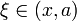 при
при 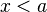 или
или 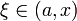 при
при  :
: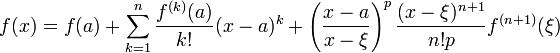
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Ряд Лорана
Необходимо
перенести в эту статью содержимое
статьи Теорема
Лорана и
поставить перенаправление. Ряд
Лорана —
двусторонне бесконечный степенной ряд
по целым степеням ![]() ,
то есть ряд вида
,
то есть ряд вида
![]()
Этот ряд понимается как сумма двух рядов:
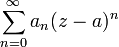 — правильная
часть ряда
Лорана и
— правильная
часть ряда
Лорана и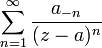 — главная
часть ряда
Лорана.
— главная
часть ряда
Лорана.
При этом, ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части.
СвойстваПравить
Eсли внутренность области сходимости ряда Лорана непуста, то она представляет собой круговое кольцо
![]()
Во всех точках своего кольца сходимости
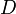 ряд
Лорана сходится абсолютно;
ряд
Лорана сходится абсолютно;Как и для степенных рядов, поведение ряда Лорана в точках граничных окружностей кольца сходимости может быть самым разнообразным;
На любом компактном множестве
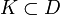 ряд сходится
равномерно;
ряд сходится
равномерно;Сумма ряда Лорана в есть аналитическая функция
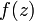 ;
;Ряд Лорана можно дифференцировать и интегрировать в почленно;
Разложение в ряд Лорана единственно, то есть если суммы двух рядов Лорана совпадают в , то совпадают и все коэффициенты этих рядов.
Коэффициенты
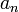 ряда
Лорана определяются через его
сумму
формулами
ряда
Лорана определяются через его
сумму
формулами
![]()
где ![]() ,
, ![]() ,
, ![]() —
любая окружность с центром a, расположенная
внутри кольца сходимости.
—
любая окружность с центром a, расположенная
внутри кольца сходимости.
ПрименениеПравить
Применение ряд Лорана основано главным образом на том (теорема Лорана), что любая однозначная аналитическая функция в кольце
![]()
представима в сходящимся рядом Лорана. В частности, в проколотой окрестности
![]()
изолированной особой точки a однозначная аналитическая функция представима рядом Лорана, который и служит основным инструментом исследования ее поведения в окрестности изолированной особой точки
