3. Виды моделей

Важным этапом моделирования является создание математической модели исследуемой системы. На базе математической модели происходит анализ характеристик системы, при компьютерном моделирования на основе математической модели создается алгоритм программ для получения информации о поведении системы. Формальное описание объекта исследование необходимо также для взаимопонимания между специалистами разных областей, объединенных для решения какой-либо глобальной задачи.

В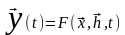 общем случае математическую модель любой динамической системы можно представить в следующем виде:

Где x - совокупность входных воздействий на систему,

h- совокупность внутренних параметров системы,

y- совокупность выходных характеристик системы,

F - закон функционирования системы.

П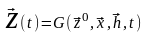 роцесс функционирования системы можно рассматривать как последовательную смену состояний: z₁(t), z₂(t)… z_k(t)

где z⁰ - совокупность начальных состояний.

Т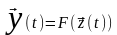 аким образом, общую математическую модель системы можно также представить следующим образом:

Все эти математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем. Однако в практике моделирование объектов на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри и т.д. Они имеют преимущества простоты и наглядности, но при существенном сужении возможностей применения. В качестве детерминированных моделей, когда при исследовании случайные факты не учитываются, для представления систем функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегро-дифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени, – конечные автоматы и конечно-разностные схемы. В качестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а для представления системы с непрерывным временем – системы массового обслуживания и т.д. В ряде некоторых случаев более перспективным является применение агрегатных моделей. Агрегативные модели позволяет описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей.

4. Математическое моделирование задач термоупругости

Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации 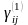отнесенные к системе прямоугольных осей х1 x2 x3 определяются выражением 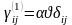(1.1.1)

, (1.1.1)

Допускается, что достаточно мало для того, чтобы термические свойства тела оставались постоянными на том отрезке времени, который нас интересует. Суммарная деформация тела выражается через компоненты вектора перемещения u1 следующим уравнением:

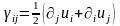(1.1.2)

где 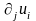обозначает частную производную .
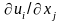