28. Substituce mezi faktory u produkční funkce. Izokvanta a přímka stejných nákladů (izokosta).

• produkční funkce firmy v dlouhém období má dva proměnlivé výrobní faktory (nejčastěji práci a kapitál)

Izokvanta (= izoprodukční křivka) - představuje takové kombinace výrobních faktorů, jejichž pomocí může firma vyrobit stejný objem produkce

• izokvanty mají klesající a konvexní tvar

Mezní míra technické substituce výrobních faktorů (kapitálu a práce):

= poměr, v němž je možno vzájemně nahrazovat práci kapitálem, aniž by se změnil objem vyráběné produkce

_K

M MTS_K,L =

_L

• určuje sklon izokvanty

Izokosta (= přímka stejných nákladů) - znázorňuje všechny kombinace výrobních faktorů, které jsou firmě maximálně dostupné při daných celkových nákladech

I … celková investice

P_L … cena práce L_max = I / P_L

P_K … cena kapitálu K_max = I / P_K

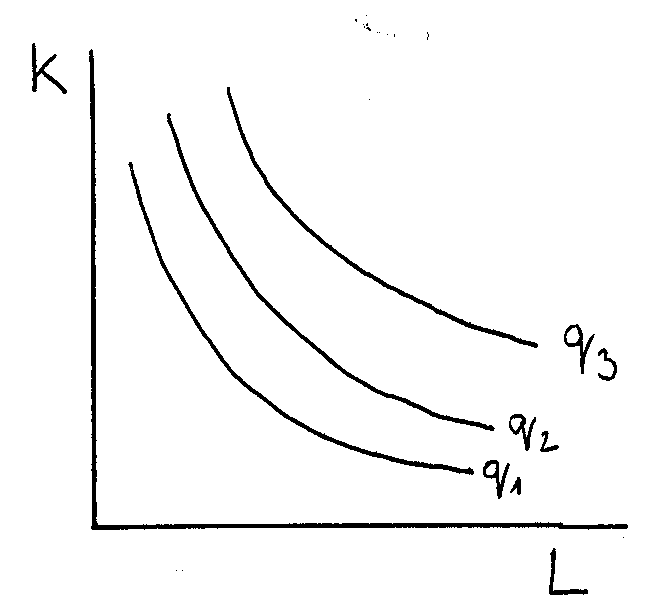
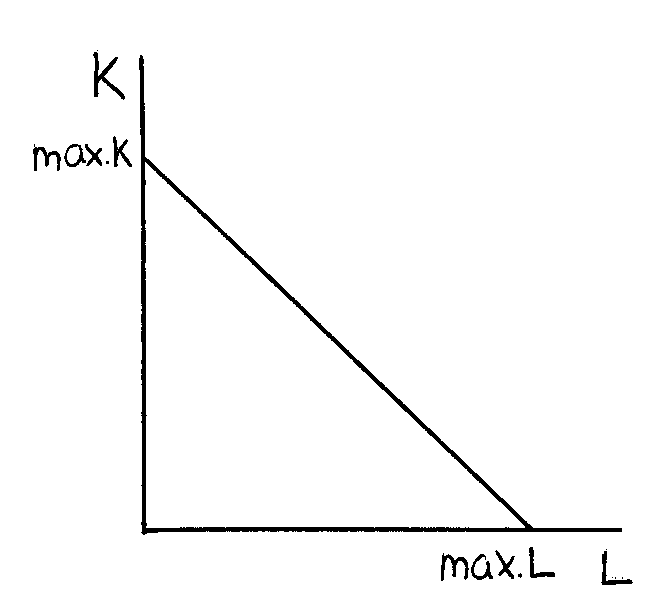
mapa izokvant

izokosta

Nákladové optimum firmy:

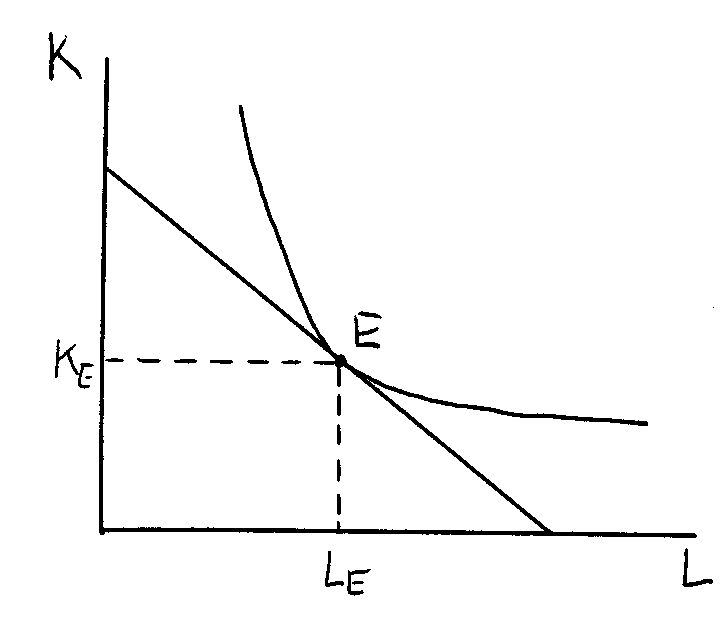= bod, ve kterém se izokvanta dotýká izokosty

• v bodě E platí:

MP_L P_L

=

MP_K P_K

MP_L … derivace Q podle L

MP_K … derivace Q podle K

29. Nákladová funkce firmy a její základní formy. Fixní a variabilní náklady. Vztahy mezi produkčními funkcemi a funkcemi technologických nákladů V různých případech produkčních a nákladových funkcí.

celkové náklady: TC = P₁X₁ + P₂X₂ + … + P_nX_n

P₁ … cena prvního výrobního faktoru

X₁ … první výrobní faktor (např. počet pracovníků)

TC = FC + VC

FC .. fixní náklady - nemění se s rozsahem vyráběného Q (např. nájemné, odpisy)

VC … variabilní náklady - mění se s rozsahem Q (např. náklady na materiál)

průměrné náklady: AC = TC / Q

• vyjadřují náklady na vyrobení jedné jednotky produktu

mezní náklady: MC = derivace TC podle Q

• vyjadřují náklady na další přírůstek jednotky vyráběného produktu

Základní typy nákladových funkcí firmy u jednotlivých produkčních funkcí:

l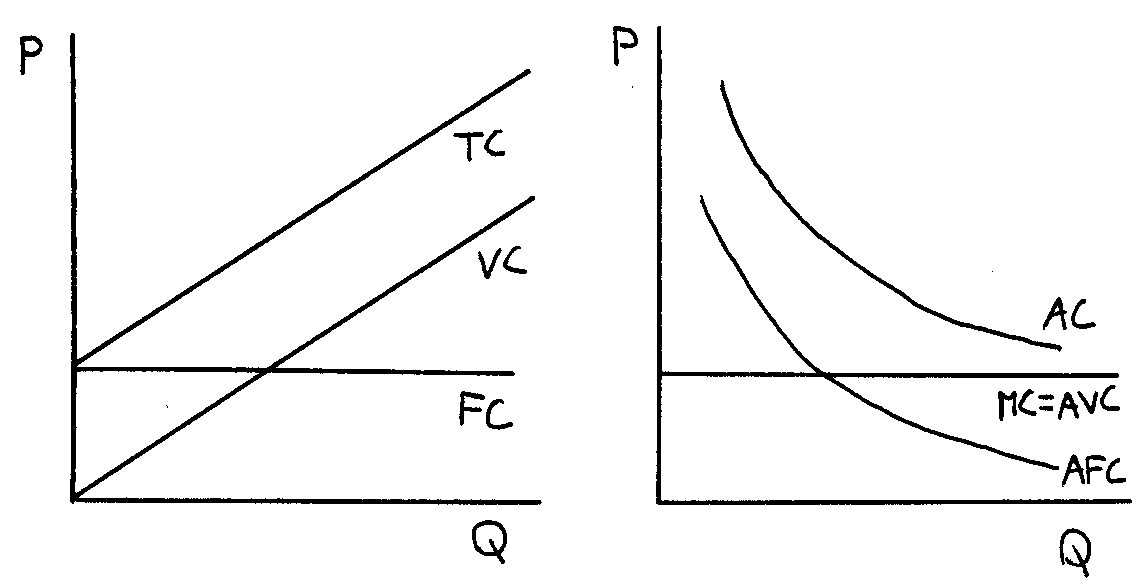 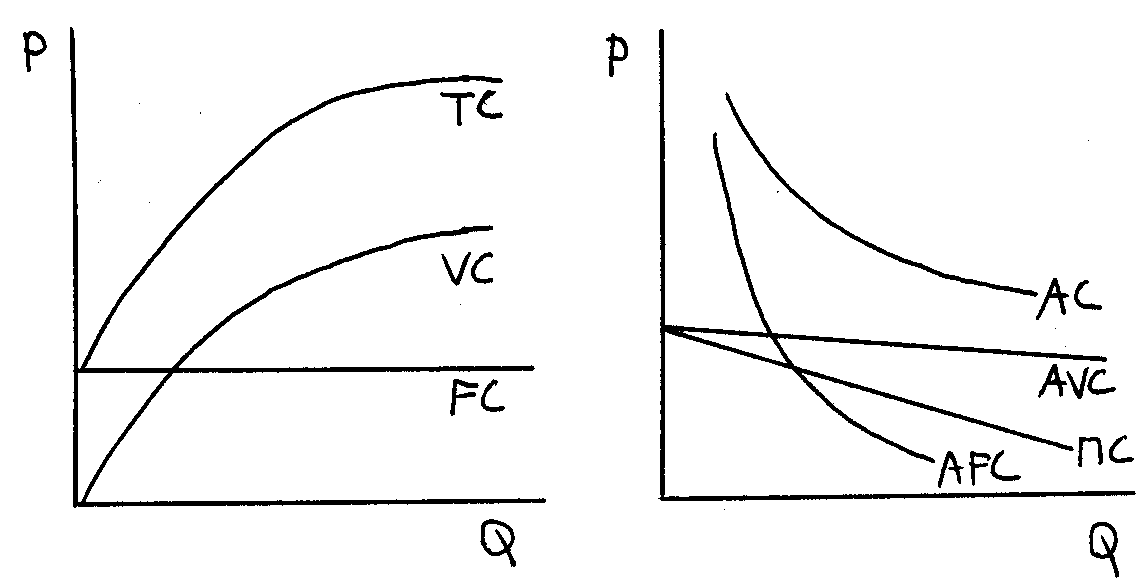ineární produkční funkce progresivní produkční funkce

TC = a + bQ AC = a/Q +b TC = a + bQ - cQ² AC = a/Q + b - cQ

VC = bQ AVC = MC = b VC = bQ - cQ² AVC = b - cQ

FC = a AFC = a/Q FC = a AFC = a/Q MC = b - 2cQ

degresivní produkční funkce progresivně degresivní produkční funkce

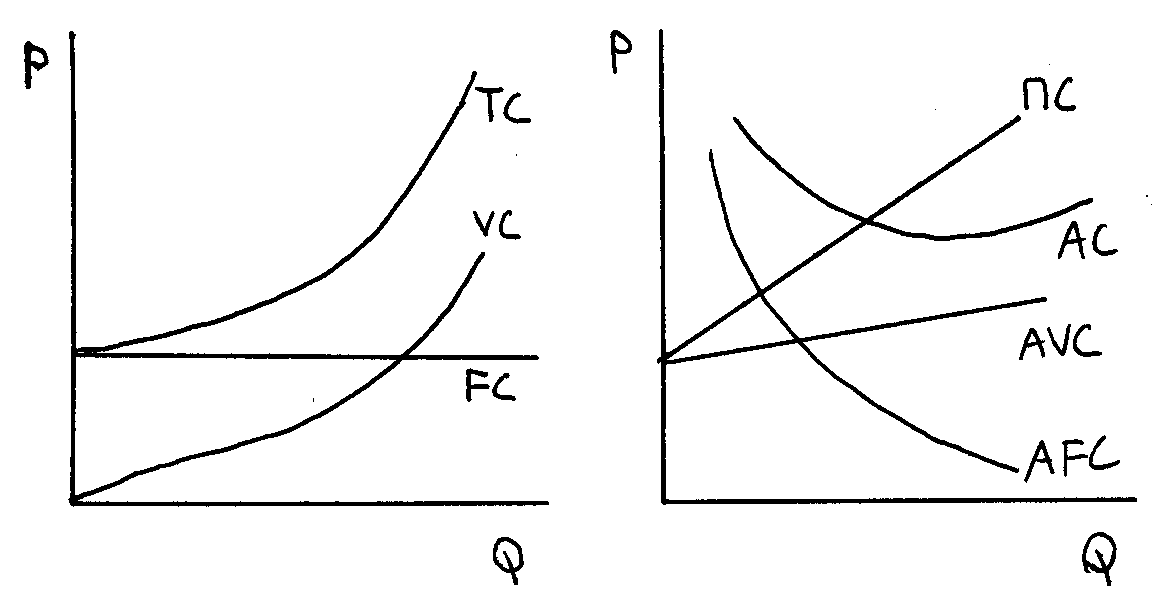
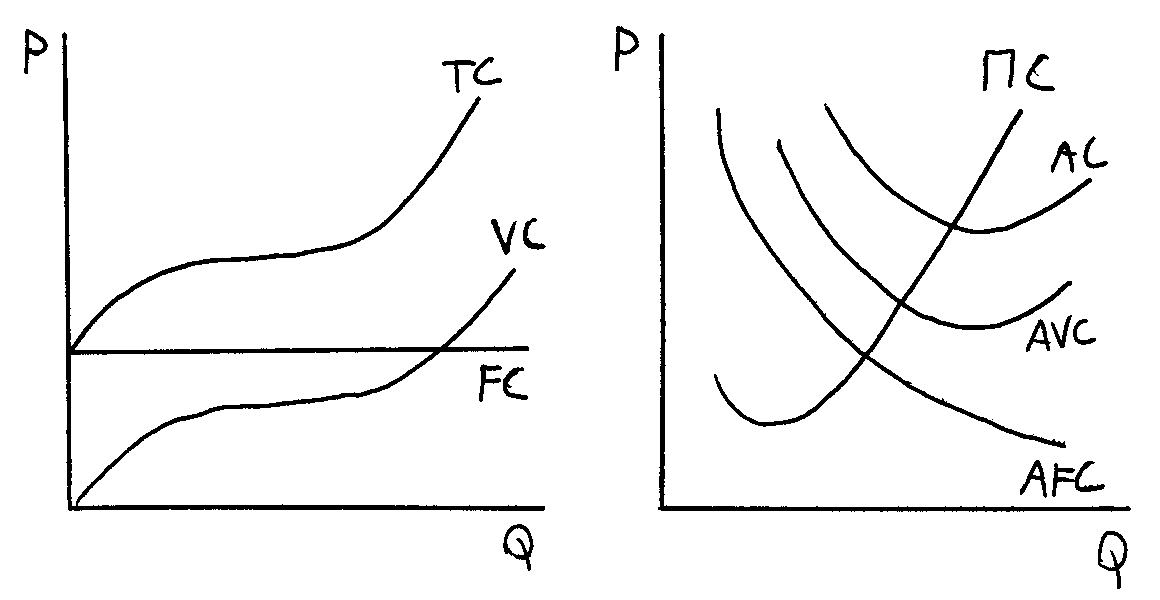
TC = a + bQ + cQ² AC = a/Q + b + cQ

VC = bQ + cQ² AVC = b + cQ

FC = a AFC = a/Q MC = b + 2cQ

Funkce technologických nákladů u jednotlivých typů produkčních a nákladových funkcí:

• jedná se vždy o inverzní funkce k produkční funkci (vyjádří se daný výrobní faktor)

• lineární produkční funkce

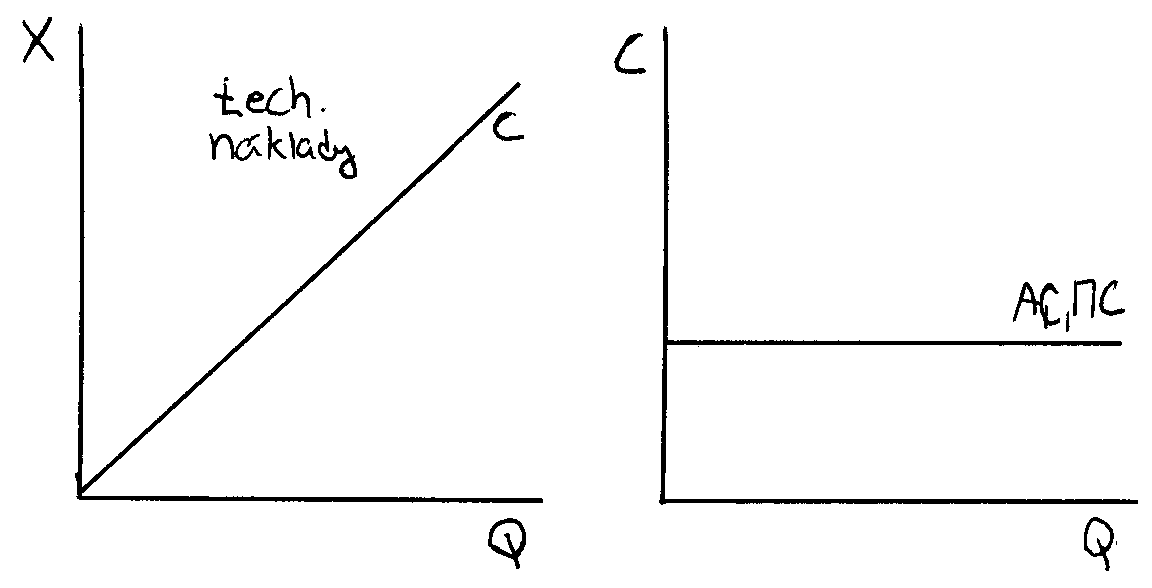
X = 1/a  Q

AC = 1/a

MC = 1/a

• progresivní produkční funkce

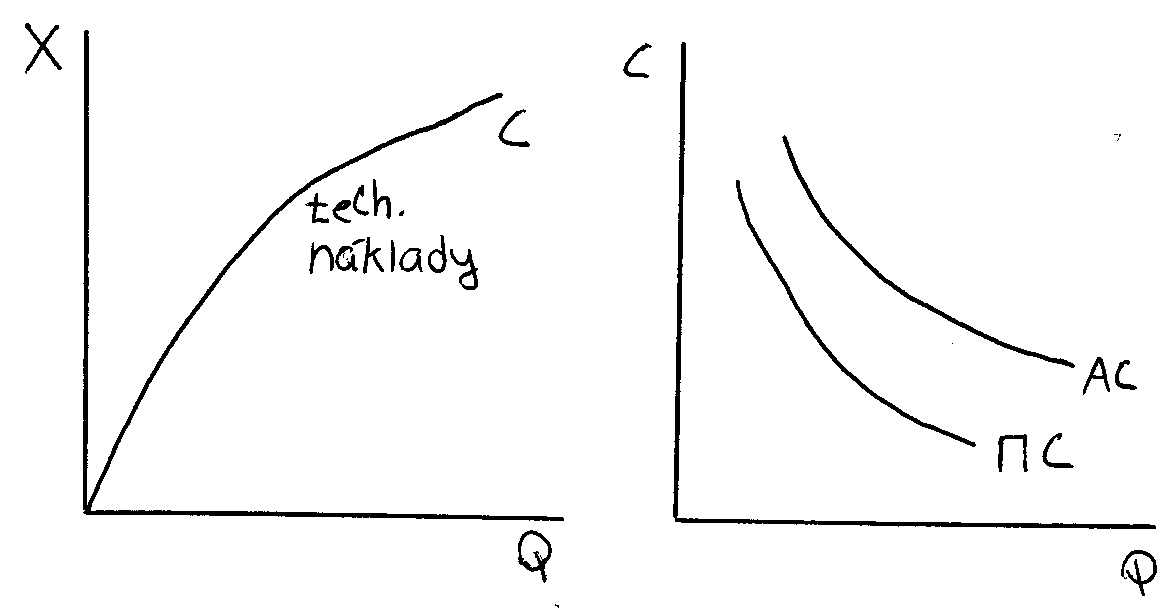
X = ^Q

AC = 1/^Q

MC = 1/  1/^Q

• degresivní produkční funkce

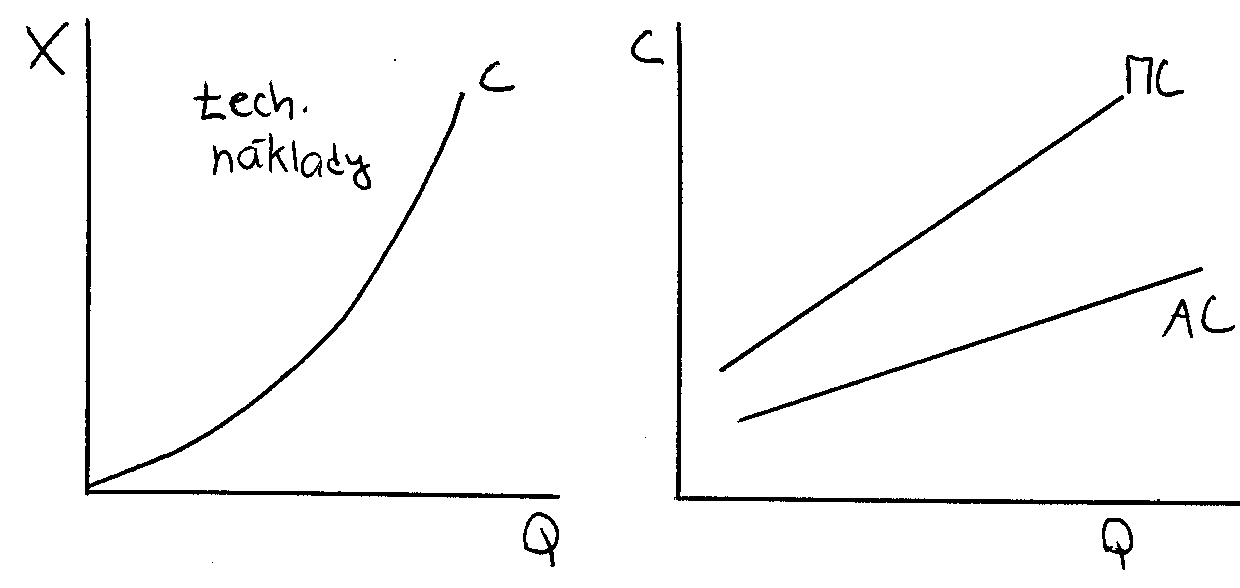
X = ^Q

AC = 1/^Q

MC = 1/  1/^Q

• progresivně degresivní produkční funkce

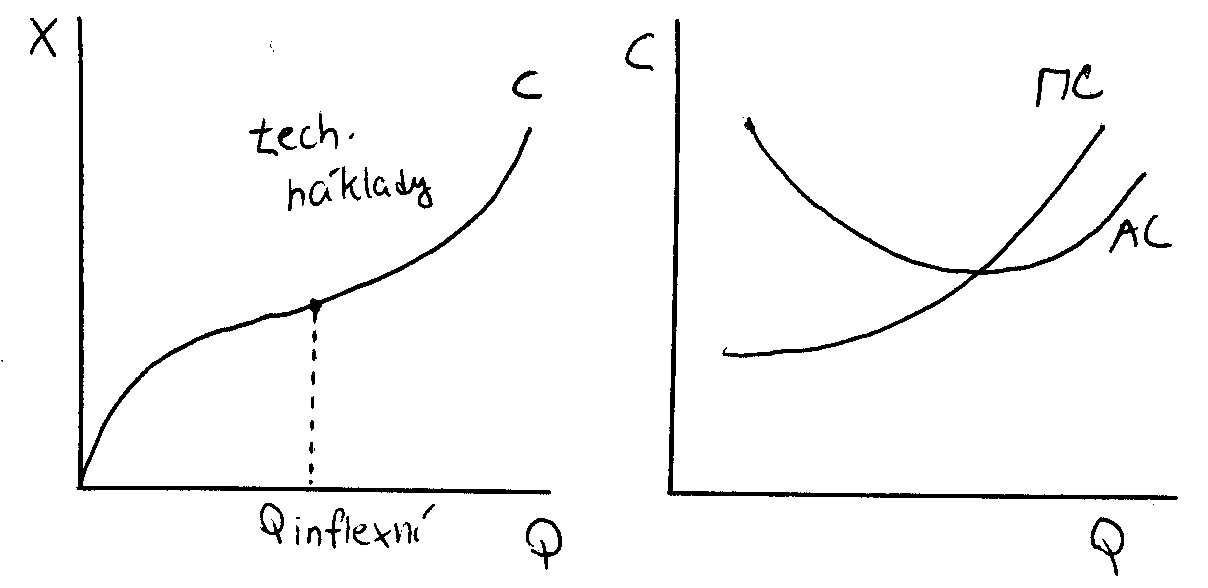
X = f (Q)

AC = X / Q

MC = X / Q