§ 2.4. Расчет сечений по разрушающим нагрузкам

В результате обширных исследований, проведенных советскими учеными (А. Ф. Лолейт, А. А. Гвоздев и др.), в начале 30-х годов был разработан метод, учитывающий упругопластические свойства железобетона, который был включен в нормы проектирования железобетонных конструкций в 1938 г.

• В основу метода расчета сечений по разрушающим нагрузкам была положена работа конструкций в III стадии напряженно-деформированного состояния, при этом предполагалось, что напряжения в бетоне и арматуре достигают предельных значений. В отличие от метода расчета по допускаемым напряжениям, где напряжения в бетоне и арматуре определялись по действующему в сечении внешнему усилию, в рассматриваемом методе по принятым напряжениям в сечении, установленным на основания экспериментов, определялось значение разрушающего усилия. Метод позволял назначать общий для всего сечения коэффициент запаса. Допускаемая нагрузка находилась путем деления разрушающей нагрузки на этот коэффициент. Метод более правильно отражал действительную работу сечений, подтверждался экспериментально и явился крупным шагом в развитии теории железобетона.

Общим недостатком обоих рассмотренных выше методов являлось использование единого коэффициента запаса, лишь весьма приближенно учитывающего многообразие факторов, влияющих на работу конструкции. Кроме того, метод расчета по разрушающим нагрузкам, позволяя достоверно определять прочность конструкции, не давал возможности оценить ее работу на стадиях, предшествующих разрушению, в частности при эксплуатационных нагрузках. Впрочем, до определенного периода практика и не ставила перед исследователями такой задачи. Это объясняется тем, что применялись сталь и бетон относительно низкой прочности, конструкции имели развитые сечения, прогибы и трещины в бетоне от эксплуатационных нагрузок были невелики и не препятствовали нормальной работе конструкций. С появлением бетона и арматуры более высокой прочности сечения уменьшались, снижалась и их жесткость, в результате чего прогибы конструкций от фактических нагрузок оказывались значительными, создавая в ряде случаев препятствия нормальной эксплуатации. Кроме того, более существенную роль стал играть фактор раскрытия трещин, вызывающий коррозию стали, к которой высокопрочная арматура особенно чувствительна. Последние два обстоятельства наряду с отмеченными выше недостатками существовавших методов потребовали дальнейшего совершенствования методики расчета железобетонных конструкций.

§ 2.5. Расчет сечений по предельным состояниям

С 1955 г. расчет железобетонных конструкций в России производится по методу предельных состояний.

• Под предельным понимают такое состояние конструкции, после достижения, которого дальнейшая эксплуатация становится невозможной вследствие потери спо­собности сопротивляться внешним нагрузкам или получения недопустимых перемещений или местных повреждений. В соответствии с этим установлены две группы предельных состояний: первая — по несущей способности; вторая — по пригодности к нормальной эксплуатации.

• Расчет по первой группе предельных состояний выполняется с целью предотвращения разрушения конструкций (расчет по прочности), потери устойчивости формы конструкции (расчет на продольный изгиб) или ее положения (расчет на опрокидывание или скольжение), усталостного разрушения (расчет на выносливость).

• Расчет по второй группе предельных состояний имеет цель не допустить развитие чрезмерных деформаций (прогибов), исключить возможность образования трещин в бетоне или ограничить ширину их раскрытия, а также обеспечить в необходимых случаях закрытие трещин после снятия части нагрузки.

Расчет по первой группе предельных состояний является основным и используется при подборе сечений. Расчет по второй группе производится для тех конструкций, которые, будучи прочными, теряют свои эксплуатационные качества вследствие чрезмерных прогибов (балки, больших пролетов при относительно малой нагрузке), образования трещин (резервуары, напорные трубопроводы) или чрезмерного раскрытия трещин, приводящего к преждевременной коррозии арматуры.

Нагрузки, действующие на конструкцию, и прочностные характеристики материалов, из которых конструкция изготовлена, обладают изменчивостью и могут отличаться от средних значений. Поэтому для обеспечения того, чтобы за время нормальной эксплуатации сооружения не наступило ни одного из предельных состояний, вводится система расчетных коэффициентов, учитывающих возможные отклонения (в неблагоприятную сторону) различных факторов, влияющих на надежную работу конструкций: 1) коэффициенты надежности по нагрузке γ_f, учитывающие изменчивость нагрузок или воздействий; 2) коэффициенты надежности по бетону γ_b и арматуре γ_s. учитывающие изменчивость их прочностных свойств; 3) коэффициенты надежности по назначению конструкции γ_n, учитывающие степень ответственности и капитальности зданий и сооружений; 4) коэффициенты условий работы γ_bi и γ_si, позволяющие оценить некоторые особенности работы материалов и конструкций в целом, которые не могут быть отражены в расчетах прямым путем.

Расчетные коэффициенты устанавливают на основе вероятностно-статистических методов. Они обеспечивают требуемую надежность работы конструкций для всех стадий: изготовления, транспортирования, возведения и эксплуатации.

Таким образом, основная идея метода расчета по предельным состояниям заключается в обеспечении условия, чтобы даже в тех редких случаях, когда на конструкцию действуют максимально возможные нагрузки, прочность бетона и арматуры минимальна, а условия эксплуатации наиболее неблагоприятны, конструкция не разрушилась и не получила бы недопустимых прогибов или трещин. При этом во многих случаях удается получать более экономичные решения, нежели при расчете ранее применявшимися методами.

Нагрузки и воздействия. При проектировании следует учитывать нагрузки, возникающие при возведении и эксплуатации сооружений, а также при изготовлении, хранении и перевозке строительных конструкций.

В расчетах используют нормативные и расчетные значения нагрузок. Установленные нормами [2] наибольшие значения нагрузок, которые могут действовать на конструкцию при ее нормальной эксплуатации, называют нормативными*. Фактическая нагрузка в силу разных обстоятельств может отличаться от нормативной в большую или меньшую сторону. Это отклонение учитывается коэффициентом надежности по нагрузке.

Расчет конструкций производится на расчетные нагрузки

q₌ q_n γ_f,

где q_n — нормативная нагрузка; γ_f — коэффициент надежности по нагрузке, соответствующий рассматриваемому предельному состоянию.

При расчете по первой группе предельных состояний γ_f принимают: для постоянных нагрузок γ_f = 1,1...1,3; временных γ_f = 1,2...1,6, при расчете на устойчивость положения (опрокидывание, скольжение, всплытие), когда уменьшение веса конструкции ухудшает условия ее работы, принимают γ_f < 1.

Расчет конструкций по второй группе предельных состояний, учитывая меньшую опасность их наступления, производят на расчетные нагрузки при γ_f = l. Исключение составляют конструкции, относящиеся к I категории трещиностойкости (см. § 7.1), для которых γ_f >l.

Нагрузки и воздействия на здания и сооружения могут быть постоянными и временными. Последние в зависимости от продолжительности действия подразделяются на длительные, кратковременные и особые.

К постоянным нагрузкам относятся вес частей сооружений, в том числе вес несущих и ограждающих конструкций; вес и давление грунтов (насыпей, засыпок); воздействие предварительного напряжения.

К временным длительным нагрузкам относятся: вес стационарного оборудования — станков, моторов, емкостей, конвейеров; вес жидкостей и твердых тел, заполня­ющих оборудование; нагрузка на перекрытия от складируемых материалов и стеллажей в складах, холодильниках, книгохранилищах, библиотеках и подсобных помещениях.

В тех случаях, когда требуется учитывать влияние длительности действия нагрузок на деформации и образование трещин, к длительным нагрузкам относится часть кратковременных. Это нагрузки от кранов, снеговые нагрузки, нагрузки от лю­дей, оборудования на перекрытия жилых и общественных зданий с пониженными нормативными значениями [2]. Эти нагрузки отнесены к длительным вследствие того, что могут действовать в течение времени, достаточного, чтобы проявились деформации ползучести, увеличиваю­щие прогиб и ширину раскрытия трещин.

К кратковременным нагрузкам относятся: нагрузки от веса людей, оборудования на перекрытия жилых и общественных зданий с полными нормативными значениями; нагрузки от кранов с полным нормативным значением; снеговые нагрузки с полным нормативным значением; ветровые нагрузки, а также нагрузки, возникающие при монтаже или ремонте конструкций.

Особые нагрузки возникают при сейсмических, взрывных или аварийных воздействиях.

Здания и сооружения подвергаются одновременному действию различных нагрузок, поэтому расчет их должен выполняться с учетом наиболее неблагоприятного сочетания этих нагрузок или усилий, вызванных ими. В зависимости от состава учитываемых нагрузок различают: основные сочетания, состоящие из постоянных, длительных и кратковременных нагрузок; особые сочетания, состоящие из постоянных, длительных, кратковременных и одной из особых нагрузок.

Значения расчетных нагрузок должны умножаться также на коэффициент надежности по назначению конструкций, учитывающий степень ответственности и капитальности зданий и сооружений.

Нормативные и расчетные сопротивления бетона. Прочностные характеристики бетона обладают изменчивостью. Даже образцы из одной партии бетона покажут при испытании разную прочность, что объясняется неоднородностью его структуры и неодинаковыми условиями испытаний. На изменчивость прочности бетона в конструкциях также влияют качество оборудования, квалификация рабочих, вид бетона и другие факторы.

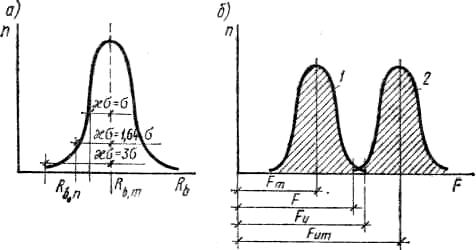
Рис. 2.3. Кривые распределения:

F_m и F — среднестатистическое и расчетное значения усилий от внешней нагрузки; F_um и F_u — то же, несущей способности

Из всех возможных значений прочности в расчет необходимо вводить такое, которое с необходимой надежностью обеспечивает безопасную эксплуатацию конструкций. Установить его помогают методы теории вероятностей.

Изменчивость прочностных свойств подчиняется, как правило, закону Гаусса и характеризуется кривой распределения (рис. 2.3, а), которая связывает прочностные характеристики бетона с частотой их повторения в опытах. Пользуясь кривой распределения, можно вычислить среднее значение временного сопротивления бетона сжатию:

R_m= (n₁R₁+ n₂R₂ + … + n_kR_k)/ n (2.7)

где n₁, n₂,.., n_k — число опытов, в которых была зафиксирована прочность R₁, R₂,…, R_k, n — общее число опытов. Разброс прочности (отклонение от среднего) характеризуется среднеквадратическим отклонением (стандартом)

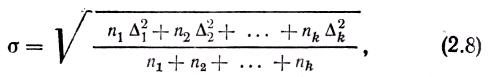
или коэффициентом вариации ν = σ/R_m. В формуле (2.8) Δ_i = R_i — R_m.

Вычислив σ, можно методами теории вероятностей найти значение прочности R_n, которое будет обеспечено с заданной надежностью (вероятностью):

где æ — показатель надежности.

Чем выше æ (см. рис. 2.3,а), тем большее число образцов покажут прочность R_m — æσ и более, тем выше надежность. Если за минимальную прочность, вводимую в расчет, принять R_n=R_m — σ (т.е. задаваясь æ = 1), то 84% всех образцов (ими могут быть кубы, призмы, восьмерки) покажут такую же или большую прочность (надежность 0,84). При æ = 1,64— 95% образцов покажут прочность R_n=R_m — 1,64σ и более, а при æ = 3 — 99,9 % образцов будут обладать прочностью не ниже R_n=R_m—Зσ [24]. Таким образом, если ввести в расчет зна­чение R_m—Зσ, то только в одном случае из тысячи прочность окажется ниже принятой. Такое явление считается практически невероятным.

Согласно нормам [1] основной контролируемой на заводе характеристикой является класс бетона «В»*, представляющий прочность бетонного куба с ребром 15 см с надежностью 0,95. Прочность, соответствующую классу, определяют по формуле (2.9) при æ =1,64

Значение ν может изменяться в широких пределах.

Заводу-изготовителю необходимо обеспечить соответствующую классу бетона прочность R_n с учетом коэффициента ν, определяемого для конкретных условий производства. На предприятиях с хорошо организованным производством (выпускающим бетон с высокой однородностью) фактический коэффициент вариации будет невелик, средняя прочность бетона [см. формулу (2.10)] может быть принята более низкой, таким образом можно сберечь цемент. Если же выпускаемый предприятием бетон имеет большую изменчивость прочности (большой коэффициент вариации), то необходимо для обеспечения требуемых значений R_n повысить прочность бетона R_m, что вызовет перерасход цемента.

При проектировании нормативное сопротивление бетона принимается численно равным призменной прочности бетона, соответствующей его классу.

* До 1984 г. основной характеристикой прочности бетона являлась его марка, которая определялась как среднее значение временного сопротивления бетона сжатию R_m в кгс/см².

Нормативное сопротивление бетонных призм осевому сжатию R_b,n (призменная прочность) определяется по нормативному значению кубиковой прочности с учетом зависимости (1.1), связывающей призменную и кубиковую прочность. Значения R_b,n приведены в табл. 2.1.

Нормативные сопротивления бетона осевому растяжению R_bt,n в случаях, когда прочность бетона на растяжение не контролируется, определяются по нормативному значению кубиковой прочности с учетом зависимости (1.2), связывающей прочность на растяжение с прочностью на сжатие. Значения R_bt,n приведены в табл. 2.1.

Если же прочность бетона на растяжение контролируется непосредственным испытанием образцов на производстве, то нормативное сопротивление осевому растяжению принимается равным

и характеризует класс бетона по прочности на растяжение.

Расчетные сопротивления бетона для предельных состояний первой группы R_b и R_bt определяют делением нормативных сопротивлений на соответствующие коэффициенты надежности бетона при сжатии γ_bc или при растяжении γ_bt:

Для тяжелого бетона γ_bc = 1,3; γ_bt = 1,5.

Эти коэффициенты учитывают возможность понижения фактической прочности по сравнению с нормативной вследствие отличия прочности бетона в реальных конструкциях от прочности в образцах и ряд других факторов, зависящих от условий изготовления и эксплуатации конструкций.

Таблица 2.1.

Прочностные и деформативные характеристики тяжелого бетона

Класс бетона по прочности на сжатие	Нормативные сопротивления и расчетные сопротивления бетона для расчета по предельным состояниям II группы, МПа		Расчетные сопротивления бетона при расчете по предельным состояниям I группы, МПа		Начальный модуль упругости бетона при сжатии Еb·10-3, МПа
	сжатию Rb,n, Rb,ser	растяжению Rbt,n, Rbt,ser	сжатию Rb	растяжению Rbt	естественного твердения	подвергнутого тепловой обработке при атмосферном давлении
В 7,5 В 10 В 12,5 В 15 В 20 В 25 В 30 В 35 В 40 В 45 В 50 В 55 В60	5,50 7,50 9,50 11,0 15,0 18,5 22,0 25,5 29,0 32,0 36,0 39,5 43,0	0,70 0,85 1,00 1,15 1,40 1,60 1,80 1,95 2,10 2,20 2,30 2,40 2,50	4,50 6,00 7,50 8,50 11,5 14,5 17,0 19,5 22,0 25,0 27,5 30,0 33,0	0,480 0,570 0,660 0,750 0,900 1,05 1,20 1,30 1,40 1,45 1,55 1,60 1,65	16,0 18,0 21,0 23,0 27,0 30,0 32,5 34,5 36,0 37,5 39,0 39,5 40,0	14,5 16,0 19,0 20,5 24,5 27,0 29,0 31,0 32,5 34,0 35,0 35,5 36,0

Расчетные сопротивления бетона для предельных состояний II группы R_b,ser и R_bt,ser определяются при коэффициентах надежности γ_bc = γ_bt = 1, т.е. принимаются равными нормативным сопротивлениям. Это объясняется тем, что наступление предельных состояний II группы менее опасно, чем I группы, поскольку оно, как правило, не приводит к обрушению сооружений и их элементов.

При расчете бетонных и железобетонных конструкций расчетные сопротивления бетона в необходимых случаях умножают на коэффициенты условий работы γ_bi, учитывающие: длительность действия и повторяемость нагрузки, условия изготовления, характер работы конструкции и т. п. Например, с целью учета снижения прочности бетона, имеющего место при длительной нагрузке, вводят коэффициент γ_b2 = 0,85...0,9, при учете нагрузок малой длительности — γ_b2 = 1,1 [1].

■ Нормативные и расчетные сопротивления арматуры. Нормативные сопротивления арматуры R_sn принимают равными наименьшим контролируемым значениям [1]: для стержневой арматуры, высокопрочной проволоки и арматурных канатов — пределу текучести, физическому σ_y, или условному σ_0,2; для обыкновенной арматурной проволоки — напряжению, составляющему 0,75 от временного сопротивления разрыву, так как ГОСТ не регламентирует предела текучести для этой проволоки.

Значения нормативных сопротивлений R_sn принимают в соответствии с действующими стандартами на арматурные стали, как и для бетона, с надежностью 0,95 (табл. 2.2).

Расчетные сопротивления арматуры растяжению R_s и R_s,ser для предельных состояний I и II группы (табл. 2.2) определяются делением нормативных сопротивлений на соответствующие коэффициенты надежности по арматуре γ_s:

Коэффициент надежности устанавливают, чтобы исключить возможность разрушения элементов в случае чрезмерного сближения R_s и R_sn. Он учитывает изменчивость площади поперечного сечения стержней, раннее развитие пластических деформаций арматуры и т.п. Его значение для стержневой арматуры классов A-I, A-II составляет 1,05; классов A-III — 1,07...1,1; классов A-IV, A-V—1,15; классов A-VI — 1,2; для проволочной арматуры классов Bp-I, B-I — 1,1; классов В-II, Вр-II, К-7, К-19—1,2.

При расчете по предельным состояниям II группы значение коэффициента надежности для всех видов ар­матуры принято равным единице, т.е. расчетные сопротивления R_s,ser численно разны нормативным.

При назначении расчетных сопротивлений арматуры сжатию R_sc учитываются не только свойства стали, но и предельная сжимаемость бетона. Принимая ε_bcu = 2Х·10^-3, модуль упругости стали E_s = 2·10^-5 МПа, можно получить наибольшее напряжение σ_sc, достигаемое в арматуре перед разрушением бетона из условия совместных деформаций бетона и арматуры σ_sc = ε_bcu E_s = ε_sE_s. Согласно нормам [1] расчетное сопротивление арматуры сжатию R_sc принимают равным R_s, если оно не превышает 400 МПа; для арматуры с более высоким значением R_s, расчетное сопротивление R_sc принимают 400 МПа (или 330 МПа при расчете в стадии обжатия). При длительном действии нагрузки ползучесть бетона приводит к повышению напряжения сжатия в арматуре. Поэтому если расчетное сопротивление бетона принимают с учетом коэффициента условий работы γ_b2 = 0,85...0,9 (т.е. с учетом продолжительного действия нагрузки), то допускается при соблюдении соответствующих конструктивных требований [1] повышать значение R_sc до 450 МПа для сталей класса A-IV и до 500 МПа для сталей классов Ат-IV и выше.

При расчетах конструкций по I группе предельных состояний расчетные сопротивления арматуры в необходимых случаях умножаются на коэффициенты условий работы γ_si, учитывающие неравномерность распределения напряжений в сечении, наличие сварных соединений, многократное действие нагрузки и др. Например, работа высокопрочной арматуры при напряжениях выше условного предела текучести учитывается коэффициентом условий работы γ_s6, величина которого зависит от класса арматуры и изменяется от 1,1 до 1,2 (см. § 4.2).

Таблица 2.2.

Прочностные и деформативные характеристики

арматурных сталей и канатов.

Класс арматуры	Диаметр, мм	Нормативные Rsn и расчетные сопротивления при расчете по предельным состояниям II группы Rs,ser, мПа	Расчетные сопротивления арматуры, МПа, при расчете по предельному состоянию I группы			Модуль упругости Es, 105 МПа
			растяжению		сжатию Rsc
			продольной и поперечной при расчете наклонных сечений на действие изгибающего момента Rs	поперечной при расчете наклонных сечений на действие поперечной силы Rsw
Стержневая
A-I	6…40	235	225	175	225	2,1
A-II	10…80	295	280	225	280	2,1
A-III	6…8	390	355	285	355	2,0
	10…40	390	365	290	365	2,0
A-IV	10…28	590	510	405	400	1,9
A-V	10…32	785	680	545	400	1,9
A-VI	10…28	980	815	650	400	1,9
A-IIIв (с контролем удлинения и напряжения)	20…40	540	490	390	200	1,8
Проволочная
Вр-I	3...5	410...395	375...360	270...260	375...360	1,7
В-II	3...8	1490...1100	1240...915	990...730	400	2,0
Вр-II	3...8	1460...1020	1215...850	970...680	400	2,0
Канатная
К-7	6...15	1450...1290	1210...1080	965...865	400	1,8
К-19	14	1410	1175	940	400	1,8

Примечание. В таблице под классами стержневой арматуры подразумевают все виды арматуры соответствующего класса, например, под классом А-V подразумевают также А_т-V, А_т-VCK и т. п.

■ Основные положения расчета.

• При расчете по I группе предельных состояний (несущей способности) должно выполняться условие

F<F_U. (2.14)

Левая часть выражения (2.14) представляет собой расчетное усилие, равное практически возможному максимальному усилию в сечении элемента при невыгоднейшей комбинации расчетных нагрузок или воздействий; оно зависит от усилий, вызванных расчетными нагрузками q при γ_f>1, коэффициентов сочетаний и коэффициентов надежности по назначению конструкций γ_n. Рас­четное усилие F не должно превышать расчетную несущую способность сечения F_u, которая является функцией расчетных сопротивлений материалов и коэффициентов условий работы γ_bi, γ_si, учитывающих неблагоприятные или благоприятные условия эксплуатации конструкций, а также формы и размеры сечения.

Кривые (рис. 2.3,б) распределения усилий от внешней нагрузки 1 и несущей способности 2 зависят от изменчивости рассмотренных выше факторов и подчиняются закону Гаусса. Выполнение условия (2.14), выраженного графически, гарантирует требуемую несущую способность конструкции.

При расчете по II группе предельных состояний:

• по перемещениям — требуется, чтобы прогибы от нормативной нагрузки f не превышали предельных значений прогибов f_u , установленных нормами для данного конструктивного элемента f ≤ f_u. Значение f_u принимают по [1];

• по образованию трещин — усилие от расчетной или нормативной нагрузки должно быть меньше или равно усилию, при котором возникают трещины в сечении F ≤ F_crc;

• по раскрытию нормальных и наклонных трещин — ширина их раскрытия на уровне растянутой арматуры должна быть меньше установленного нормами [1] предельного их раскрытия a_crc,u a_crc ≤ _acrc,u = 0,l...0,4 мм.

В необходимых случаях требуется, чтобы трещины, образовавшиеся от полной нагрузки, были бы надежно закрыты (зажаты) при действии длительной ее части. В этих случаях производится расчет по закрытию трещин.

? 1. Стадии напряженно-деформированного состояния изгибаемых железобетонных элементов. Какие из этих стадий используются при расчете прочности, трещиностойкости, прогибов? 2. Особенности напряженно-деформированного состояния предварительно напряженных конструкций. 3. Основные положения методов расчета сечений по допускаемым напряжениям и разрушающим нагрузкам. Недостатки этих методов. 4. Основные положения расчета по методу предельных состояний. Группы предельных состояний. 5. Каковы цели расчета по I и II группам предельных состояний? 6. Классификация нагрузок и их расчетные сочетания. 7. Нормативные и расчетные нагрузки. Коэффициенты надежности по нагрузкам. В каких пределах они изменяются? 8. Нормативное сопротивление бетона. Как оно связано со средней прочностью? С какой обеспеченностью оно назначается? 9. Как определяется расчетное сопротивление бетона для I и II групп предельных состояний? С какой целью вводятся коэффициенты надежности и коэффициенты условий работы? 10. Как назначается нормативное сопротивление арматуры для различных сталей? 11. Расчетные сопротивления арматуры, коэффициенты надежности и условий работы. 12. Запишите в общем виде условия, исключающие наступление предельных состояний I и II групп, и объясните их смысл.