Статистические меры информации
При статическом вероятностном подходе получение конкретного количества информации рассматривается как результат определенного выбора среди возможных сообщений. Получатель информации может заранее знать или угадать ее часть. Когда приходит сообщение о часто происходящих событиях, вероятность появления которых Р стремится к единице, то такое сообщение малоинформативно. Столь же малоинформативны в среднем сообщения о событиях, вероятности которых стремятся к нулю, т.е. о почти невозможных событиях, поскольку сообщения о таких событиях поступают чрезвычайно редко.
События можно рассматривать как возможные исходы некоторого опыта. Все исходы составляют полную группу событий, или ансамбль.
Семантические меры информации
Используются для измерения смыслового содержания информации. Наибольшее распространение здесь получила тезаурусная мера, связывающая семантические свойства информации со способностью пользователя принимать поступившее сообщение.
Тезаурус— это совокупность сведений, которыми располагает пользователь или система.
Относительной мерой семантической информации может служить коэффициент содержательности C, который определяется как отношение количества семантической информации к ее объему:
.
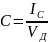Прагматическая мера информации. Определяет ее полезность, ценность для достижения пользователем поставленной цели. Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе.
11. Основные функции компьютера. Схема работы компьютера
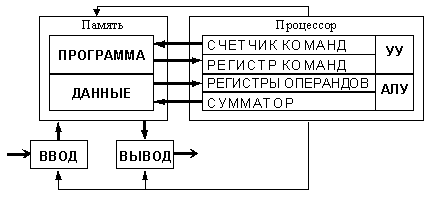
Основные функции компьютера – это ввод, хранение и обработка информации. Последовательность действий в ЭВМ при решении задач повторяет действие человека. Любую ЭВМ образуют три главных устройства: устройства ввода-вывода, оперативная память, процессор. Эти устройства соединены каналами связи, по которым передается информация.
Функции устройств ввода- вывода: ввод, вывод информации.
Функции памяти: прием информации из других устройств, запоминание информации, выдача информации по запросу.
Функции процессора: выполнение расчетов (такое устройство называется арифметико - логическое устройство (АЛУ), управление всеми устройствами ЭВМ (такое взаимодействие реализуется устройством управления (УУ)). Обычно эти два устройства (АЛУ и УУ) выделяются чисто условно, конструктивно они не разделены и являются частью устройства, называемого процессор.
В составе процессора также имеется ряд специальных запоминающих ячеек, называемых регистрами. Регистр выполняет две функции:
1) Кратковременное хранение числа или команды.
2) Выполнение над ними некоторых операций.
Некоторые важные регистры имеют свои собственные названия:
Счетчик команд - регистр УУ, содержимое которого соответствует адресу очередной выполняемой команды; служит для автоматической выборки программы из последовательных ячеек памяти.
Регистр команд – регистр УУ для хранения кода команды на период времени, необходимый для ее выполнения. Часть его разрядов используется для хранения кода выполняемой операции, остальные для хранения кодов адресов операндов.
Сумматор – электронно – логическая схема, выполняющая суммирование двоичных чисел.
12. Команда, схема взаимодействия. Выполнение команды
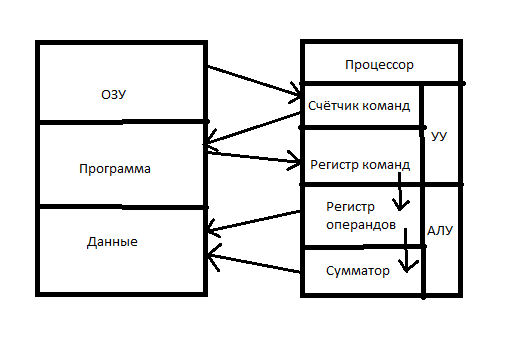
Команда
Программа - это упорядоченная последовательность команд, предназначенных для решения задачи. Команда – это описание элементарных операций, которые должна выполнить ЭВМ.
Выполнение команды
Как правило, этот процесс разбивается на следующие этапы:
1) из ячейки памяти, адрес которой храниться в счетчике команд, выбирается очередная команда. Содержимое счетчика команд увеличивается на длину команды;
2) выбранная команда передается в устройство управления на регистр команд;
3) УУ расшифровывает адресное поле команды;
4) по сигналам УУ операнды выбираются из памяти в АЛУ на специальные регистры операндов;
5) УУ расшифровывает код операции и выдает сигналы АЛУ выполнить соответствующую операцию над данными;
6) результат операции либо остается в процессоре, либо отправляется в память, если в команде был указан адрес результата;
7) все предыдущие этапы повторяются до достижения команды «конец».
13. Системы счисления (основание, полином, понятие разряда, длина числа)
Система счисления - совокупность приемов и правил изображения чисел цифровыми знаками. Системы счисления делятся на непозиционные и позиционные.
Непозиционная система счисления - система, в которой значение символа не зависит от его положения в числе. Непозиционные системы счисления возникли раньше позиционных систем. Они использовались в древности римлянами, египтянами, славянами и другими народами.
Основной недостаток непозиционных систем - большое число различных знаков и сложность выполнения арифметических операций.
Позиционная система счисления - система, в которой значение символа зависит от его места в ряду цифр, изображающих число.
Основание (базис) позиционной системы счисления – количество знаков или символов, используемых в разрядах для изображения числа в данной системе счисления (q).
Для позиционной системы счисления с общим основанием справедливо равенство:
P(q)=an*qn
+
an-1*qn-1
+…+ a1*q1
+ a0*q0
+ a-1*q-1
+…+ a-m*q-m=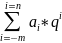
,
где q -основание позиционной системы счисления;
P(q) - произвольное число;
an - коэффициент ряда( цифры системы счисления);
n,m - количество целых и дробных разрядов.
Возможно множество позиционных систем, так как за основание можно принять любое целое число.
Вес разряда pi числа в позиционной системе счисления есть отношение вида pi= qi/q0, где i - номер разряда справа налево.
Если разряд имеет вес pi= qi,то следующий старший разряд будет иметь вес pi+1 = qi-1, а предыдущий младший разряд-вес pi-1 = qi-1, таким образом, в позиционной системе счисления вес разряда определяется его положением(позицией) в числе.
Длина числа - количество разрядов(позиций) в записи числа.
001101011 - 9 разрядов, 235961 - 6 разрядов.
Длина разрядной сетки (n) - термин, используемый для определения длины числа. В разных системах счисления длина разрядной сетки при записи одного и того же числа неодинаковая. Например,
9610 = 1408 =11000002. Xmax = qn - 1.
Диапазон представления (ДП) чисел в заданной системе счисления - интервал числовой оси, заключенный между максимальными и минимальными числами, представленными длиной разрядной сетки.
14. Перевод чисел из одной системы счисления в другую
Наиболее часто мы пользуемся десятичной системой счисления , однако при работе с вычислительной техникой возникает необходимость перевода чисел, записанных в десятичной системе, в произвольную систему счисления и, наоборот. Существуют достаточно простые правила преобразования записи числа из одной системы счисления в другую.
Рассмотрим правила перевода чисел из любой системы счисления в систему счисления с произвольным основанием. Пусть N - число, которое будем переводить; q - основание системы счисления, в которую будем переводить.
Случай N - целое положительное число ( N>=1 )
Общее правило перевода числа из системы с основанием р в систему с основанием q можно сформулировать следующим образом:
Число N делим на новое основание q . Полученный от деления первый остаток является младшей цифрой целой части числа в системе с основанием q . Целую часть полученного числа снова делим на основание q . В результате определим второй остаток, равный следующей после младшей цифре числа в системе с основанием q . Деление проводим до тех пор, пока не получим частное, меньшее делителя. Последнее частное дает старшую цифру числа в системе с основанием q Действия производим в той системе счисления, из которой переводим.
Случай 0 < N <1
Необходимо найти неотрицательные целые коэффициенты
a-1,, a-2, . . . , a-m , каждый из которых меньше q , такие, что
Np = a -1 q -1 + a -2 q -2 + . . . + a -m q -m .
Можно сформулировать следующее правило перевода правильной дроби с основанием р в дробь с основанием q .
Умножаем Np на q и берем a -1 , равной целой части результата умножения Np на q , умножаем полученную дробную часть на q и берем в качестве a -2 целую часть результата и т.д. Действия производим в системе счисления с основанием р, т.е. в той системе счисления, из которой переводим.
Случай перевода нецелых чисел, больших 1.
Перевод чисел, имеющих целую и дробную части, выполняется в два этапа: вначале переводится целая часть, а затем - дробная.
15. Перевод чисел из любой системы счисления в десятичную и наоборот
Перевод чисел из любой системы счисления в десятичную можно осуществить, используя свойство позиционной системы счисления ( представление любого числа в позиционной системе в виде многочлена по степеням основания ) и выполняя действия над числами, представленными в десятичной системе.
-
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
6
0110
7
0111
8
1000
9
1001
A
1010
B
1011
C
1100
D
1101
E
1110
F
1111
При переводе чисел из десятичной системы счисления в любую другую, всегда отдельно (по разным правилам) переводится целая и дробная части.